
4.“气备四时,与天地明鬼神合其德;教重万世,继尧舜禹汤文武人之师。”下列各项中与对联所写的历史人物主张无关的是
A、“有教无类” B、“因材施教” C、“己所不欲,勿施于人” D、“法不阿贵”
3.康熙五十二年(1713),康熙帝派人入藏册封五世班禅罗桑益喜为“班禅额尔德尼”,从此正式确立了“班禅额尔德尼”这个称号以及班禅在西藏的政教地位。康熙帝这一做法的主要目的是
A.加强满、藏民族的团结
B.确立罗桑益喜在西藏的政教地位
C.巩固清廷对西藏地区的统治 D.宣扬自己对喇嘛教的崇信
2.易中天在《帝国的终结》中说“秦,虽死犹存,它亡得悲壮。”从政治上看“秦,虽死犹存”主要是指
A.统一度量衡、货币
B.开创皇帝制度
C.中央建立三公九卿制
D.建立统一国家和中央集权制
1.诏版是中国古代皇帝的一种诏书形式。有一中国古代某朝代的刀刻诏版,其正面书刻小篆体40字,即“廿六年,皇帝尽并兼天下诸侯,黔首大安,立号为皇帝。乃诏丞相状、绾(状、绾均为人名),法度量则不壹,歉疑者,皆明壹之”。据诏书内容推断,与该诏版相关的朝代最有可能是
A.秦朝 B.西汉 C.唐朝 D.明朝
(17)(本小题满分8分)设数列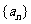 是等比数列,
是等比数列,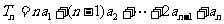 ,已知
,已知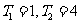 , (1)求数列
, (1)求数列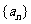 的首项和公比;(2)求数列
的首项和公比;(2)求数列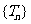 的通项公式。
的通项公式。
(18)(本小题满分10分)已知数列 {an} 的各项均为正数,且满足a2=5,
an+1 = an2-2n an+2,(n Î N*). 推测并证明an的通项公式.
(19)(本小题满分10分)已知数列{an}中,a1 =1,前 n 项和为Sn,且点(an,an+1)在直线
x-y+1=0上. 计算+++…+.
(20)(本小题满分12分)某县与沙漠化进行长期的斗争. 全县面积为 p, 2002 年底绿化率达 ,从 2003 年开始,每年绿化原有沙漠面积的 ,但与此同时,原有绿化面积的 被沙化. 设2002 年底的绿化面积为 a1,经过 n 年后的绿化面积为 an+1 .
(I) 求2003年底的绿化面积
(II ) 经过多少年后,绿化率达?
(13) 已知{an}为等差数列,a1 =2, S10=110. 设an =log0.5 bn ( n Î N*),则{bn}的各项和为 .
(14) 微处理器在诞生后的25年之内,非常准确地遵循“摩尔定律”:半导体芯片每18个月集成度翻番,价格减半. 半导体芯片价格降低,必然导致电脑价格降低. 若每4年电脑的价格降低三分之一,则现价为8100元的电脑12年后价格可能降为 .
(15) 在等比数列中,a9 + a10 = a (a ≠ 0), a19 + a20 = b,则a99 + a100等于 .
(16) 对于n Î N*,若{an}是等差数列,则数列{}也是等差数列.类比上述性质,相应地,若{bn}是正项等比数列,则数列 也是等比数列.
(1) 等差数列 -3,1,5,…的第15 项的值是 (A) 40 (B) 53 (C) 63 (D) 76
(2) 等差数列{an} 中,a3 =2,则该数列的前5项的和为 (A)10 (B) 16 (C) 20 (D)32
(3) 数列 1, , , … , 的各项和为
(A) (B) (C) (D)
(4) 已知数列{an}满足a1 =0,an+1 = an+2n,那么a2005的值是 (A)2003×2004 (B)2004×2005 (C) 20052 (D) 2005×2006
(5) 已知数列 {an}(n Î N)中,a1 = 1,an+1 = ,则an 为 (A) 2n-1 (B) 2n + 1 (C) (D)
(6) 在等比数列 {an} 中, a7 a11 =6, a4 +a14 =5, 则=
(A) (B) (C) 或 (D) -或-
(7) =
(A)0 (B) (C)1 (D) 不存在
(8) 小丁储备2008年赴京观看奥运会的费用,他从2001年起到2007年,每年元旦到银行存入a元一年定期储蓄,若年利率r保持不变,且每年存款到期自动转存新的一年定期. 到2008年元旦将所有的存款和利息悉数取出,可提取
(A) a(1+r)8元 (B) [(1+r)7-(1+r)]元 (C) [(1+r)8-1]元 (D) [(1+r)8-(1+r)]元
(9) 已知{an}是等差数列,{bn}是正项等比数列,其公比q≠1,若a1 = b1,a11 = b11,则 (A) a6<b6 (B) a6 >b6 (C) a6≤ b6 (D) a6≥b6
(10) 等差数列{an}的前n项和为Sn,若a1 >0,S4 =S8,则当Sn取得最大值时,n的值为
(A) 5 (B)6 (C) 7 (D) 8
(11) 数列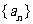 的前n项和为
的前n项和为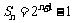 ,那么该数列前2n项中所有奇数位置的项的和为
,那么该数列前2n项中所有奇数位置的项的和为
(A)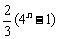 (B)
(B)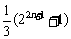 (C)
(C)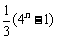 (D)
(D)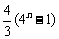
(12) 等差数列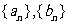 的前n项的和分别为
的前n项的和分别为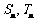 ,若
,若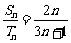 ,则
,则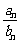 =
=
(A)1
(B)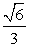 (C)
(C)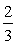 (D)
(D)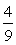
求函数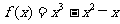 的极值和单调区间.
的极值和单调区间.
(18)(本小题满分10分)
设函数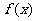 是定义在
是定义在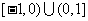 上的奇函数,当
上的奇函数,当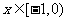 时,
时,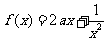
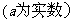
(Ⅰ)当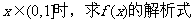 ;
;
(Ⅱ)若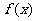 在
在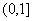 上为增函数,求
上为增函数,求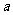 的取值范围.
的取值范围.
(19)(本小题满分10分)
设函数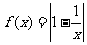 ,点P(x0,y0)
,点P(x0,y0)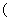 0<x0<1
0<x0<1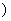 在曲线
在曲线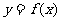 上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
上,求曲线在点P处的切线与x轴和y轴的正向所围成的三角形面积表达式(用x0表达).
(20)(本小题满分12分)
某厂生产某种电子元件,如果生产出一件正品,可获利200元,如果生产出一件次品则损失100元.已知该厂制造电子元件过程中,次品率p与日产量x的函数关系是: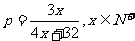 .
.
(I)将该厂的日盈利额T(元)表示为日产量x(件)的函数;
(II)为获得最大盈利,该厂的日产量应为多少件?
(14)函数y=x-2sinx在(0, 2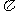 )内的单调增区间为
.
)内的单调增区间为
.
(15)曲线y=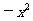 上的点到直线2x-y+3=0的最短距离为
.
上的点到直线2x-y+3=0的最短距离为
.
(16)向高为8m,底面边长为8m的倒置正四棱锥形的容器内注水,其速度为每分钟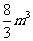 ,则 当水深为5m时,水面上升的速度为
.
,则 当水深为5m时,水面上升的速度为
.
(1)已知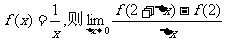 的值是
的值是
(A)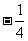 (B)2
(C)
(B)2
(C)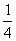 (D)-2
(D)-2
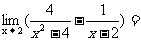
(2)
(A)0
(B) (C)
(C)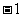 (D)
(D)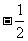
(3)已知曲线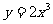 ,则过点(1,2)的切线的斜率是
,则过点(1,2)的切线的斜率是
(A)2 (B)4 (C)6 (D)8
(4)函数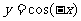 的导数是
的导数是
(A)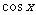 (B)
(B)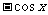 (C)
(C)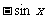 (D)
(D)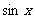
(5)若函数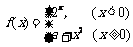 为R上的连续函数,则a 的值为
为R上的连续函数,则a 的值为
(A)2 (B)1 (C)0 (D)-1
(6)下列给出的四个命题中,正确的命题是
①若函数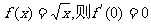
②若函数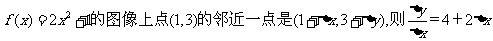
③瞬时速度是动点位移函数S(t)对时间t的导数
④曲线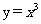 在点(0,0)处没有切线
在点(0,0)处没有切线
(A)①② (B)②③ (C)①②③ (D)②③④
(7)函数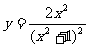 的导数是
的导数是
(A)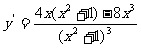 (B)
(B)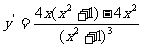
(C)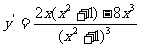 (D)
(D)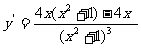
(8)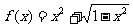 为增函数的区间是
为增函数的区间是
(A)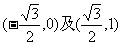 (B)
(B)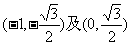
(C)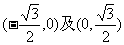 (D)
(D)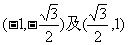
(9)函数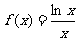 的最大值为
的最大值为
(A)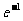 (B)e
(C)
(B)e
(C)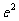 (D)10
(D)10
(10)半径为r的圆形铁板,受热膨胀,半径r为时间t的函数,其导数(半径膨胀率)为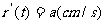 那么其面积的膨胀率
那么其面积的膨胀率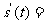
(A)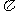 (B)
(B)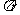 (C)
(C)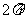 (D)
(D)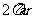
(11)若f(x)是在(-L,L)内的可导的偶函数,且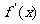 不恒为0,则
不恒为0,则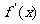
(A)必定是(-L,L)内的偶函数
(B)必定是(-L,L)内的奇函数
(C)必定是(-L,L)内的非奇非偶函数
(D)可能是(-L,L)内的奇函数,可能是偶函
(12)已知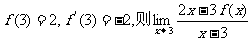 的值是
的值是
(A)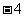 (B)0
(C)8
(D)不存在
(B)0
(C)8
(D)不存在
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com