4. 函数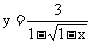的定义域是　　　　　　　　　 　　。

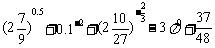3. 的值为 　　　　　　。

2．集合A={(x，y)|y=x+2}，集合B={(x，y)|y=x² }，则A∩B=_。

1. 已知集合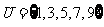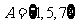，，则_。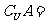

22.(本小题12分)已知f(x)＝(x²+ax+a)e^－x(a≤2，x∈R)．

(1)当a＝1时，求f(x)的单调区间；

(2)是否存在实数a，使f(x)的极大值为3？若存在，求出a的值，若不存在，说明理由．

解析：(1)当a＝1时，f(x)＝(x²+x+1)e^－x；f′(x)＝e^－x(－x²+x)．

当f′(x)＞0时，0＜x＜1.

当f′(x)＜0时，x＞1或x＜0.

∴f(x)的单调递增区间为(0,1)，

单调递减区间为(－∞，0)和(1，+∞)．

(2)f′(x)＝(2x+a)e^－x－e^－x(x²+ax+a)＝e^－x[－x²+(2－a)x]．

令f′(x)＝0，得x＝0或x＝2－a，列表如下：

由表可知f(x)_极大＝f(2－a)＝(4－a)e^a－2.

设g(a)＝(4－a)e^a－2，g′(a)＝(3－a)e^a－2＞0，

∴g(a)在(－∞，2)上是增函数，

∴g(a)≤g(2)＝2＜3

∴(4－a)e^a－2≠3

∴不存在实数a使f(x)最大值为3.

选择题答案

DBCDB BBCCB　 AD

21．(本小题12分)已知函数f(x)＝log₄(4^x+1)+kx(k∈R)是偶函数．

(1)求k的值；

(2)若方程f(x)－m＝0有解，求m的取值范围．

解析：由函数f(x)是偶函数，可知f(x)＝f(－x)，

∴log₄(4^x+1)+kx＝log₄(4^－x+1)－kx，

即log₄＝－2kx，log₄4^x＝－2kx，

∴x＝－2kx对一切x∈R恒成立．∴k＝－.

(2)由m＝f(x)＝log₄(4^x+1)－x，

∴m＝log₄＝log₄(2^x+)．

∵2^x+≥2，∴m≥.

故要使方程f(x)－m＝0有解，m的取值范围为m≥.

20.(本小题12分)已知命题p：∀m∈[－1,1]，有a²－5a－3≥恒成立，命题q：∃x∈R，使x²+ax+2＜0，若p是真命题，q是假命题，求a的取值范围．

解析：∵m∈[－1,1]，

∴∈[2，3]，

∵∀m∈[－1,1]，

有a²－5a－3≥恒成立，

∴a²－5a－3≥3，∴a≥6或a≤－1，

故命题p为真命题时，a≥6或a≤－1，

又命题q：∃x∈R，使x²+ax+2＜0，

即不等式x²+ax+2＜0有解，

∴Δ＝a²－8＞0，

∴a＞2或a＜－2，

若命题q为假命题，

则－2≤a≤2，

∴命题p为真命题，q为假命题，a的取值范围为－2≤a≤－1.

19．(本小题12分)已知函数f(x)＝2sinxcosx－2cos²x+1，

(1)求f(x)的最大值及相应的x的值；

(2)若f(θ)＝，求cos2(－2θ)的值．

解析：(1)f(x)＝sin2x－(2cos²x－1)＝sin2x－cos2x＝sin(2x－)，

∴当2x－＝2kπ+，即x＝kπ+π(k∈Z)时，f(x)取得最大值.

(2)由f(θ)＝sin2θ－cos2θ，及f(θ)＝得sin2θ－cos2θ＝，

两边平方得1－sin4θ＝，即sin4θ＝；

∴cos2(－2θ)＝cos(－4θ)＝sin4θ＝.

18.(本小题12分) 已知函数f(x)＝x³－2ax²+3x(x∈R)．

(1)若a＝1，点P为曲线y＝f(x)上的一个动点，求以点P为切点的切线斜率取最小值时的切线方程；

(2)若函数y＝f(x)在(0，+∞)上为单调增函数，试求满足条件的最大整数a.

解析：(1)设切线的斜率为k，

则k＝f′(x)＝2x²－4x+3＝2(x－1)²+1，

当x＝1时，k_min＝1.又f(1)＝，

所以所求切线的方程为y－＝x－1，

即3x－3y+2＝0.

(2)f′(x)＝2x²－4ax+3，要使y＝f(x)为单调递增函数，

必须满足f′(x)＞0，即对任意的x∈(0，+∞)，恒有f′(x)＞0，f′(x)＝2x²－4ax+3＞0，

∴a＜＝+，而+≥，

当且仅当x＝时，等号成立．

所以a＜，

所求满足条件的a值为1.

17．(本小题10分)已知函数f(x)＝2sin(π－x)cosx，

(1)求f(x)的最小正周期；

(2)求f(x)在区间[－，]上的最大值和最小值．

解析：(1)∵f(x)＝2sin(π－x)cosx＝2sinxcosx＝sin2x，

∴函数f(x)的最小正周期为π.

(2)由－≤x≤⇒－≤2x≤π，

∴－≤sin2x≤1，

∴f(x)在区间[－，]上的最大值为1，最小值为－.