
2.△ABC中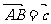 ,
,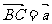 ,
,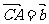 ,
,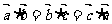 ,则△ABC的形状为 .
,则△ABC的形状为 .
1.已知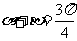 ,则
,则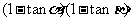 的值是_____
的值是_____
9.设两个非零向量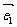 和
和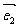 不共线.
不共线.
(1)如果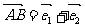 ,
,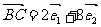 ,
,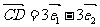 ,求证:
,求证: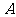 、
、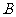 、
、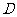 三点共线;
三点共线;
(2)若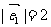 ,
,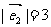 ,
,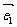 与
与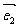 的夹角为
的夹角为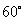 ,是否存在实数
,是否存在实数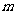 ,使得
,使得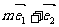 与
与 垂直?并说明理由.
垂直?并说明理由.
江苏省泗阳中学高三数学课本基础知识回归(必修4之2)
班级 姓名 得分
8.若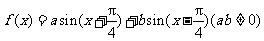 是偶函数,则a+b=
.
是偶函数,则a+b=
.
7.已知定义在R上的奇函数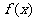 在区间
在区间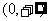 上单调递增,若
上单调递增,若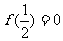 ,△
,△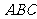 的内角A满足
的内角A满足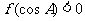 ,则A的取值范围是
.
,则A的取值范围是
.
6.已知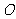 为原点,点
为原点,点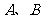 的坐标分别为
的坐标分别为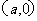 ,
,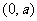 其中常数
其中常数 ,点
,点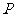 在线段
在线段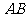 上,且
上,且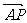 =
=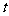
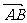 (
(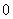 ≤
≤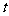 ≤
≤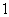 ),则
),则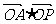 的最大值为 .
的最大值为 .
5.有下列四种变换方式:
①向左平移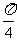 ,再将横坐标变为原来的
,再将横坐标变为原来的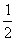 ; ②横坐标变为原来的
; ②横坐标变为原来的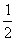 ,再向左平移
,再向左平移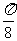 ;
;
③横坐标变为原来的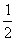 ,再向左平移
,再向左平移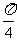 ; ④向左平移
; ④向左平移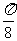 ,再将横坐标变为原来的
,再将横坐标变为原来的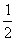 ;
;
其中能将正弦曲线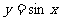 的图像变为
的图像变为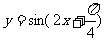 的图像的是 .
的图像的是 .
4.已知扇形的周长为L,则当扇形的圆心角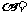 时,扇形面积S最大=
.
时,扇形面积S最大=
.
3.函数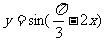 的单调递减区间是 .
的单调递减区间是 .
2.已知向量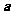 =
=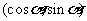 ,
,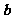 =
=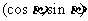 ,且
,且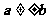 ,那么
,那么 与
与 的夹角的大小是 度.
的夹角的大小是 度.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com