
21.(本小题满分12分)
.已经数列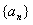 的前n项和
的前n项和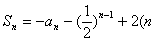 为正整数).
为正整数).
(Ⅰ)令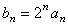 ,求证数列
,求证数列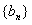 是等差数列,并求数列
是等差数列,并求数列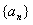 的通项公式;
的通项公式;
(Ⅱ)令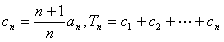 ,试比较
,试比较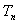 与
与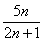 的大小,并予以证明.
的大小,并予以证明.
20. (本小题满分12分)
对于在[m,n]上有意义的两个函数f(x)与g(x),如果对于任意的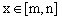 ,均有
,均有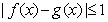 ,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数
,则称f(x)与g(x)在[m,n]上是接近的,否则称f(x)与g(x)在[m,n]上是非接近的.现有两个函数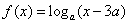 与
与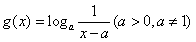 ,给定区间[a+2,a+3].
,给定区间[a+2,a+3].
(1)若f(x)与g(x)在给定区间[a+2,a+3]上都有意义,求a的范围;
(2)判断f(x)与g(x)在给定区间[a+2,a+3]上是否接近?
19. (本小题满分12分)
已知向量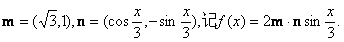

(1)若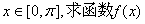 的值域;
的值域;
(2)在△ABC中,角A、B、C所对的边分别为a、b、c,若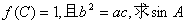 的值。
的值。
18. (本小题满分12分)
甲、乙二人进行一次围棋比赛,约定先胜3局者获得这次比赛的胜利,比赛结束,假设在一局中,甲获胜的概率为0.6,乙获胜的概率为0.4,各局比赛结果相互独立,已知前2局中,甲、乙各胜1局。
(Ⅰ)求甲获得这次比赛胜利的概率;
(Ⅱ)设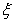 表示从第3局开始到比赛结束所进行的局数,求
表示从第3局开始到比赛结束所进行的局数,求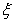 的分布列及数学期望.
的分布列及数学期望.
17. (本小题满分12分)
已知函数f(x)=
sin(2x+ ) (A>0,|
) (A>0,| |<
|<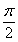 ),且f(
),且f(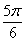 )=-1,
)=-1,
(1). 求 的值;
的值;
(2).若f(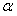 )=
)= ,f(
,f(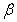 +
+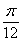 )=
)=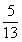 ,且
,且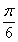 <
<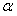 <
<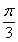 ,0<
,0<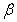 <
< ,
, 
求cos(2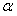 +2
+2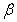 -
-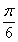 )的值
)的值

16. 下列命题:(1)等比数列{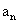 }是递增数列的充要条件是公比q>1; (2)△ABC为钝角△,则cosA<sinB;
(3)函数y=f(x+1)的图象与函数y=f(3-x) 的图象关于直线x=1对称;(4)定义在R上的奇函数f(x)的图象关于直线x=1对称,则函数f(x) 为周期函数且周期为4;(5)平面上有四点A,B,C,O,且
}是递增数列的充要条件是公比q>1; (2)△ABC为钝角△,则cosA<sinB;
(3)函数y=f(x+1)的图象与函数y=f(3-x) 的图象关于直线x=1对称;(4)定义在R上的奇函数f(x)的图象关于直线x=1对称,则函数f(x) 为周期函数且周期为4;(5)平面上有四点A,B,C,O,且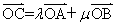 ,则
,则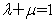 是A,B,C三点共线的充要条件;其中正确命题是
(写出所有正确命题的序号).
是A,B,C三点共线的充要条件;其中正确命题是
(写出所有正确命题的序号).

15. 已知数列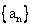 的通项公式
的通项公式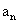 =
=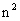 cosn
cosn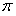 ,
,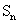 为它的前n项和,则
为它的前n项和,则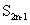 =
。
=
。
14. 已知sin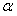 +sin
+sin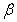 =1,则sin
=1,则sin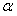 sin
sin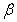 +sin
+sin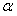 的取值范围是
。
的取值范围是
。
13. 已知向量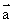 ,
,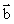 满足|
满足|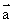 |=1,|
|=1,|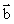 | =2,且(
| =2,且(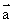 -
-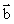 )
)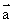 =0,则
=0,则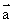 与
与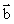 的夹角为 。
的夹角为 。
12. 若函数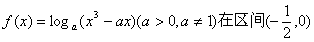 内单调递增,则a的值范围是 A.
内单调递增,则a的值范围是 A.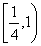 B.
B.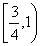 C.
C.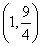 D.
D.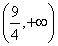

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com