
(二)填空题
1. (安徽卷理15)若
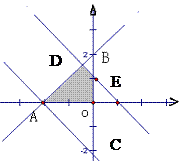
(安徽卷理15)若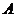 为不等式组
为不等式组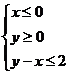 表示的平面区域,则当
表示的平面区域,则当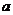 从-2连续变化到1时,动直线
从-2连续变化到1时,动直线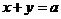 扫过
扫过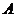 中的那部分区域的面积为
中的那部分区域的面积为
解析:如图知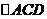 是斜边为3 的等腰直角三角形,
是斜边为3 的等腰直角三角形,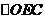 是直角边为1等腰直角三角形,区域的面积
是直角边为1等腰直角三角形,区域的面积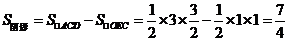
2.(广东卷文12)若变量x,y满足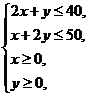 则z=3x+2y的最大值是________。
则z=3x+2y的最大值是________。
[解析]画出可行域,利用角点法可得答案70.
3. (全国Ⅰ卷理13文13)若
(全国Ⅰ卷理13文13)若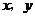 满足约束条件
满足约束条件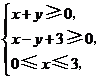 则
则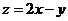 的最大值为
.
的最大值为
.
答案:9.如图,作出可行域,
作出直线 ,将
,将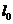 平移至过点
平移至过点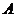 处
处
时,函数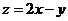 有最大值9.
有最大值9.
4.(山东卷文16)设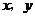 满足约束条件
满足约束条件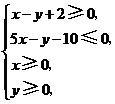 则
则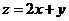 的最大值为
.
的最大值为
.
解析:本小题主要考查线性规划问题。作图(略)易知可行域为一个四角形,其四个顶点
分别为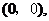
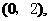
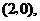
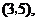 验证知在点
验证知在点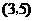 时取得最大值11.
时取得最大值11.
5.(上海卷文11)在平面直角坐标系中,点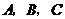 的坐标分别为
的坐标分别为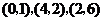 .如果
.如果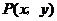 是
是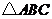 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当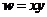 取到最大值时,点
取到最大值时,点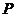 的坐标是 ______ .
的坐标是 ______ .
[解析]作图知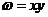 取到最大值时,点
取到最大值时,点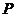 在线段BC上,
在线段BC上,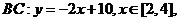
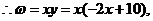 故当
故当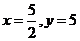 时,
时, 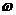 取到最大值. [答案]
取到最大值. [答案]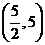
6.(浙江卷理17)若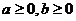 ,且当
,且当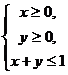 时,恒有
时,恒有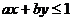 ,则以
,则以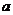 ,b为坐标点P(
,b为坐标点P(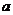 ,b)所形成的平面区域的面积等于____________。
,b)所形成的平面区域的面积等于____________。
 [答案]
[答案]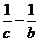
8.(福建卷理14)若直线3x+4y+m=0与圆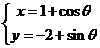 (
(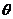 为参数)没有公共点,则实数m的取值范围是
.
为参数)没有公共点,则实数m的取值范围是
.
解:圆心为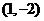 ,要没有公共点,根据圆心到直线的距离大于半径可得
,要没有公共点,根据圆心到直线的距离大于半径可得
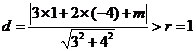 ,即
,即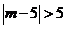 ,
,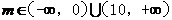
9.(福建卷文14))若直线3x+4y+m=0与圆x2+y2-2x+4y+4=0没有公共点,则实数m的取值范围是 .
解:圆心为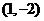 ,要没有公共点,根据圆心到直线的距离大于半径可得
,要没有公共点,根据圆心到直线的距离大于半径可得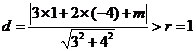 ,即
,即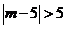 ,
,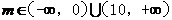
10.(广东卷理11)经过圆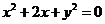 的圆心
的圆心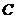 ,且与直线
,且与直线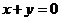 垂直的直线
垂直的直线
方程是 .
[解析]易知点C为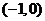 ,而直线与
,而直线与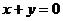 垂直,我们设待求的直线的方程为
垂直,我们设待求的直线的方程为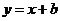 ,将点C的坐标代入马上就能求出参数
,将点C的坐标代入马上就能求出参数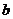 的值为
的值为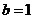 ,故待求的直线的方程为
,故待求的直线的方程为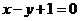 。
。
11.(广东卷理15文15)已知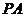 是圆
是圆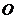 的切线,切点为
的切线,切点为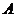 ,
,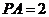 .
.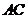 是圆
是圆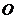 的直径,
的直径,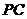 与圆
与圆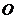 交于点
交于点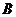 ,
,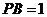 ,则圆
,则圆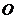 的半径
的半径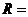 .
.
[解析]依题意,我们知道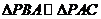 ,由相似三角形的性质我们有
,由相似三角形的性质我们有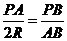 ,即
,即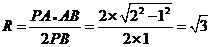 。
。
12.(湖北卷文15)圆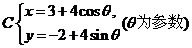 的圆心坐标为
,和圆C关于直线
的圆心坐标为
,和圆C关于直线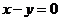 对称的圆C′的普通方程是
.
对称的圆C′的普通方程是
.
解:由题设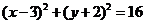 ,圆心坐标
,圆心坐标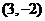 ;关于直线
;关于直线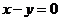 对称的圆C′圆心为
对称的圆C′圆心为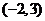 ,半径相等,所以方程是
,半径相等,所以方程是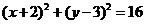
13.(湖南卷文14)将圆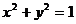 沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线
沿x轴正向平移1个单位后所得到圆C,则圆C的方程是________,若过点(3,0)的直线 和圆C相切,则直线
和圆C相切,则直线 的斜率为_____________.
的斜率为_____________.
[答案]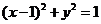 ,
, 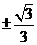
[解析]易得圆C的方程是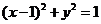 ,
,
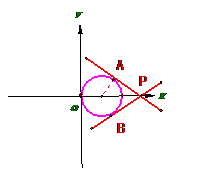 直线
直线 的倾斜角为
的倾斜角为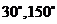 ,
,
所以直线 的斜率为
的斜率为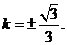
14.(四川卷理14文14)已知直线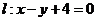 与圆
与圆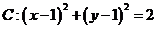 ,则
,则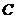 上各点到
上各点到 的距离的最小值为_______。
的距离的最小值为_______。
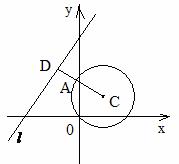 [解]:如图可知:过原心作直线
[解]:如图可知:过原心作直线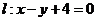 的垂线,则
的垂线,则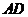 长即为所求;
长即为所求;
∵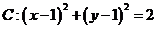 的圆心为
的圆心为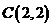 ,半径为
,半径为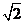
点 到直线
到直线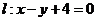 的距离为
的距离为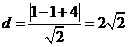
∴  故
故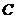 上各点到
上各点到 的距离的最小值为
的距离的最小值为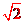
[点评]:此题重点考察圆的标准方程和点到直线的距离;
[突破]:数形结合,使用点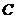 到直线
到直线 的距离距离公式。
的距离距离公式。
15.(天津卷文15)已知圆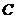 的圆心与点
的圆心与点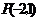 关于直线
关于直线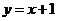 对称.直线
对称.直线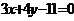 与圆
与圆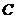 相交于
相交于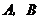 两点,且
两点,且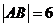 ,则圆
,则圆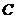 的方程为
.
的方程为
.
解析:圆心的坐标为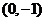 ,所以
,所以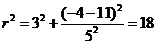 ,圆的方程为
,圆的方程为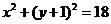 .
.
16.(重庆卷理15)直线l与圆x2+y2+2x-4y+a=0(a<3)相交于两点A,B,弦AB的中点为(0,1),则直线l的方程为 .
解:设圆心 ,直线
,直线 的斜率为
的斜率为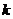 , 弦AB的中点为
, 弦AB的中点为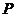 ,
,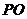 的斜率为
的斜率为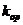 ,
,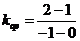 则
则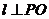 ,所以
,所以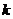
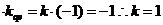 由点斜式得
由点斜式得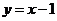
17.(重庆卷文15)已知圆C: 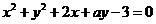 (a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=
.
(a为实数)上任意一点关于直线l:x-y+2=0的对称点都在圆C上,则a=
.
[答案]-2
[解析]本小题主要考查圆的一般方程及几何性质,由已知,直线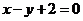 经过了圆心
经过了圆心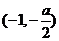 ,所以
,所以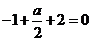 ,从而有
,从而有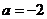 。
。
(一)选择题
1.(全国Ⅱ卷理11)等腰三角形两腰所在直线的方程分别为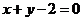 与
与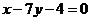 ,原点在等腰三角形的底边上,则底边所在直线的斜率为( )
,原点在等腰三角形的底边上,则底边所在直线的斜率为( )
A.3 B.2 C.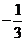 D.
D.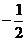
[答案]A
[解析]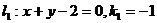 ,
,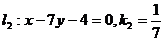 ,设底边为
,设底边为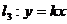
由题意,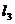 到
到 所成的角等于
所成的角等于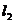 到
到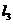 所成的角于是有
所成的角于是有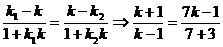
再将A、B、C、D代入验证得正确答案是A
 A.
A.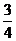 B.1 C.
B.1 C. D.5
D.5
解:如图知区域的面积是△OAB去掉一个小直角三角形。
(阴影部分面积比1大,比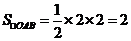 小,故选C,不需要算出来)
小,故选C,不需要算出来)
5.(北京卷理5)若实数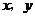 满足
满足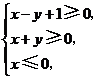 则
则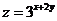 的最小值是( )
的最小值是( )
A.0 B.1 C.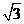 D.9
D.9
[标准答案]: B
[试题分析]: 解出可行域的顶点,带入验证。
[高考考点]: 线性规划
[易错提醒]: 顶点解错
[备考提示]: 高考基本得分点。
6.(北京卷文6)若实数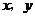 满足
满足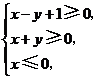 则
则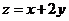 的最小值是( )
的最小值是( )
A.0 B.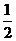 C.1
D.2
C.1
D.2
[解析]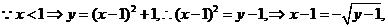
所以反函数为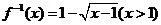 [答案]B
[答案]B
7.(福建卷理8)若实数x、y满足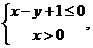 则
则 的取值范围是
的取值范围是
A.(0,1) B.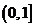 C.(1,+
C.(1,+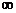 ) D.
) D.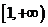
解:由已知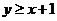 ,
,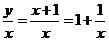 ,又
,又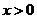 ,故
,故 的取值范围是
的取值范围是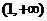
8.(福建卷文10)若实数x、y满足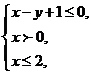 则
则 的取值范围是
的取值范围是
A.(0,2) B.(0,2) C.(2,+∞) D.[2,+∞)
解:由题设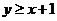 ,所以
,所以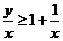 ,又
,又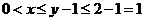 ,因此
,因此
又 可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
可看做可行域中的点与原点构成直线的斜率,画出可行域也可得出答案。
9.(广东卷理4)若变量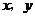 满足
满足 则
则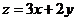 的最大值是( )
的最大值是( )
A.90 B.80 C.70 D.40
[解析]画出可行域,利用角点法易得答案C.
10.(海南宁夏卷文10)点P(x,y)在直线4x + 3y = 0上,且满足-14≤x-y≤7,则点P到坐标原点距离的取值范围是( )
A. [0,5] B. [0,10] C. [5,10] D. [5,15]
[标准答案]:B
[试题解析]:根据题意可知点P在线段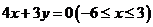 上,有线段过原点,故点P到原点最短距离为零,最远距离为点
上,有线段过原点,故点P到原点最短距离为零,最远距离为点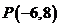 到原点距离且距离为10,故选B;
到原点距离且距离为10,故选B;
12.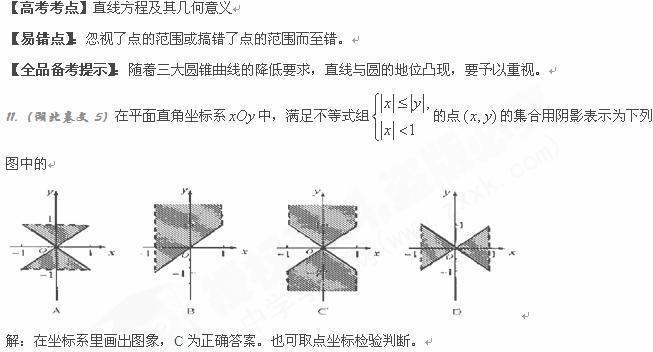 (湖南卷理3)已知变量x、y满足条件
(湖南卷理3)已知变量x、y满足条件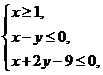 则
则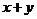 的最大值是( )
的最大值是( )
A.2 B.5 C.6 D.8
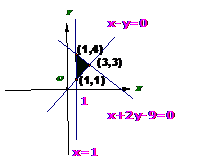 [答案]C
[答案]C
[解析]如图得可行域为一个三角形,其三个顶点
分别为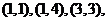 代入验证知在点
代入验证知在点
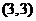 时,
时,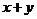 最大值是
最大值是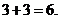
故选C.
13. (湖南卷文3)已条变量
(湖南卷文3)已条变量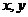 满足
满足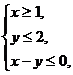 则
则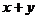 的最小值是( )
的最小值是( )
A.4 B.3 C.2 D.1
[答案]C
[解析]如图得可行域为一个三角形,其三个顶点
分别为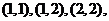 代入验证知在点
代入验证知在点
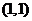 时,
时,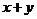 最小值是
最小值是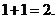 故选C.
故选C.
14.(辽宁卷文9)已知变量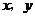 满足约束条件
满足约束条件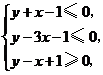 则
则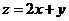 的最大值为
的最大值为
A.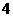 B.
B.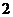 C.
C. D.
D.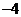
17. (陕西卷理10)已知实数
(陕西卷理10)已知实数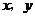 满足
满足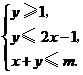 如果目标函数
如果目标函数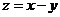 的最小值为
的最小值为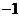 ,则实数
,则实数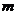 等于( )
等于( )
A.7 B.5 C.4 D.3
解:画出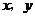 满足的可行域,可得直线
满足的可行域,可得直线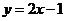 与直线
与直线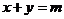 的交点使目标函数
的交点使目标函数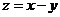 取得最小值,故
取得最小值,故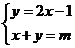 ,解得
,解得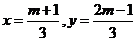 ,
,
代入 得
得
18. (天津卷理2文2)设变量
(天津卷理2文2)设变量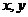 满足约束条件
满足约束条件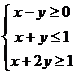 ,则目标函数
,则目标函数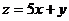 的最大值为
的最大值为
(A) 2 (B) 3 (C) 4 (D) 5
解析:如图,由图象可知目标函数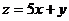 过点
过点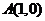 时
时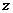 取得最大值,
取得最大值,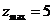 ,选D.
,选D.
19.(浙江卷文10)若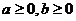 ,且当
,且当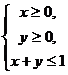 时,恒有
时,恒有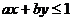 ,则以
,则以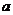 ,b为坐标点
,b为坐标点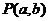 所形成的平面区域的面积等于
所形成的平面区域的面积等于
(A)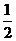 (B)
(B)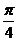 (C)1 (D)
(C)1 (D)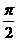
解析:本小题主要考查线性规划的相关知识。由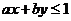 恒成立知,当
恒成立知,当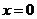 时,
时,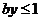 恒成立,∴
恒成立,∴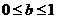 ;同理
;同理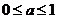 ,∴以
,∴以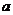 ,b为坐标点
,b为坐标点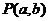 所形成的平面区域是一个正方形,所以面积为1. 答案:C
所形成的平面区域是一个正方形,所以面积为1. 答案:C
20.(安徽卷理8文10)若过点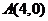 的直线
的直线 与曲线
与曲线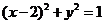 有公共点,则直线
有公共点,则直线 的斜率的取值范围为( )
的斜率的取值范围为( )
A.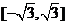 B.
B.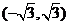 C.
C.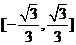 D.
D.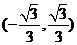
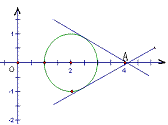 解:设直线方程为
解:设直线方程为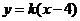 ,即
,即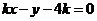 ,直线
,直线 与曲线
与曲线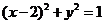 有公共点,圆心到直线的距离小于等于半径
有公共点,圆心到直线的距离小于等于半径
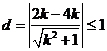 ,
,
得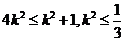 ,选择C 另外,数形结合画出图形也可以判断C正确。
,选择C 另外,数形结合画出图形也可以判断C正确。
21.(北京卷理7)过直线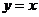 上的一点作圆
上的一点作圆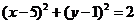 的两条切线
的两条切线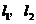 ,当直线
,当直线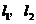 关于
关于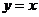 对称时,它们之间的夹角为( )
对称时,它们之间的夹角为( )
A.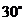 B.
B.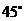 C.
C.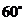 D.
D.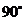
[标准答案]: C
[试题分析一]: 过圆心M作直线 :y=x的垂线交与N点,过N点作圆的切线能够满足条件,不难求出夹角为60
:y=x的垂线交与N点,过N点作圆的切线能够满足条件,不难求出夹角为60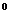 。
。
[试题分析二]:明白N点后,用图象法解之也很方便
[高考考点]: 直线与圆的位置关系。
[易错提醒]: N点找不到。
[备考提示]: 数形结合这个解题方法在高考中应用的非常普遍,希望加强训练。
22.(广东卷文6)经过圆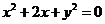 的圆心C,且与直线
的圆心C,且与直线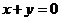 垂直的直线方程是
垂直的直线方程是
A、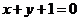 B、
B、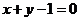 C、
C、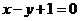 D、
D、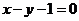
[解析]易知点C为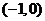 ,而直线与
,而直线与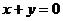 垂直,我们设待求的直线的方程为
垂直,我们设待求的直线的方程为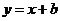 ,将点C的坐标代入马上就能求出参数
,将点C的坐标代入马上就能求出参数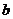 的值为
的值为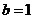 ,故待求的直线的方程为
,故待求的直线的方程为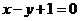 ,选C.(或由图形快速排除得正确答案.)
,选C.(或由图形快速排除得正确答案.)
23.(湖北卷理9)过点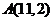 作圆
作圆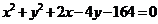 的弦,其中弦长为整数的共有
的弦,其中弦长为整数的共有
A. 16条 B. 17条 C. 32条 D. 34条
解:圆的标准方程是: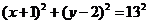 ,圆心
,圆心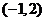 ,半径
,半径 过点
过点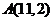 的最短的弦长为10,最长的弦长为26,(分别只有一条)还有长度为
的最短的弦长为10,最长的弦长为26,(分别只有一条)还有长度为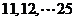 的各2条,所以共有弦长为整数的
的各2条,所以共有弦长为整数的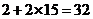 条。
条。
24.(辽宁卷理3文3)圆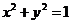 与直线
与直线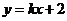 没有公共点的充要条件是( )
没有公共点的充要条件是( )
A.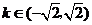 B.
B.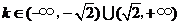
C.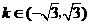 D.
D.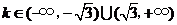
答案:C
解析:本小题主要考查直线和圆的位置关系。依题圆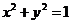 与直线
与直线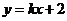 没有公共点
没有公共点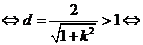
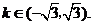
25.(全国Ⅰ卷理10)若直线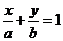 通过点
通过点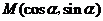 ,则( )
,则( )
A.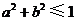 B.
B.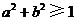 C.
C.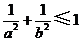 D.
D.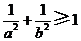
解析:D.由题意知直线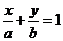 与圆
与圆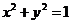 有交点,则
有交点,则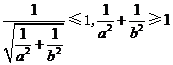 .
.
另解:设向量 ,由题意知
,由题意知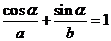
由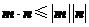 可得
可得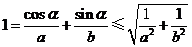
26.(全国Ⅰ卷文10)若直线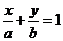 与圆
与圆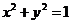 有公共点,则( )
有公共点,则( )
A.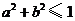 B.
B.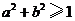 C.
C. D.
D.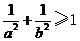
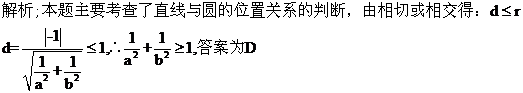
27.(山东卷理11)已知圆的方程为x2+y2-6x-8y=0.设该圆过点(3,5)的最长弦和最短弦分别为AC和BD,则四边形ABCD的面积为
(A)10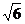 (B)20
(B)20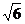 (C)30
(C)30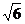 (D)40
(D)40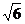
解: 化成标准方程
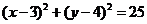 ,过点
,过点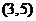 的最长弦为
的最长弦为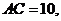
最短弦为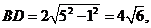
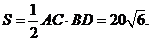
28.(山东卷文11)若圆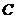 的半径为1,圆心在第一象限,且与直线
的半径为1,圆心在第一象限,且与直线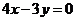 和
和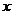 轴相切,则该圆的标准方程是( )
轴相切,则该圆的标准方程是( )
A. B.
B.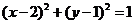
C.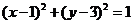 D.
D.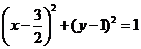
解析:本小题主要考查圆与直线相切问题。
设圆心为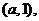 由已知得
由已知得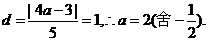 选B.
选B.
29.(陕西卷理5文5)直线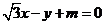 与圆
与圆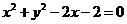 相切,则实数
相切,则实数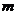 等于A.
等于A.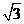 或
或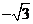 B.
B.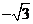 或
或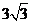 C.
C.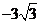 或
或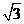 D.
D.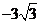 或
或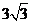
解:圆的方程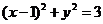 ,圆心
,圆心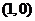 到直线的距离等于半径
到直线的距离等于半径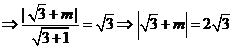
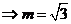 或者
或者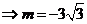
30. (上海卷理15文15)如图,在平面直角坐标系中,
(上海卷理15文15)如图,在平面直角坐标系中,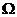 是一个与x
是一个与x
轴的正半轴、y轴的正半轴分别相切于点C、D的定圆所围成区域
(含边界),A、B、C、D是该圆的四等分点,若点P(x,y)、
P’(x’,y’)满足x≤x’ 且y≥y’,则称P优于P’,如果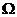 中的
中的
点Q满足:不存在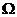 中的其它点优于Q,那么所有这样的点Q组成
中的其它点优于Q,那么所有这样的点Q组成
的集合是劣弧( )
A. B. C. D.
[答案]
[解析]依题意,在点Q组成的集合中任取一点,过该点分别作平行于两坐标轴的直线,构成的左上方区域(权且称为“第二象限”)与点Q组成的集合无公共元素,这样点Q组成的集合才为所求. 检验得:D.
31.(重庆卷理3)圆O1:x2+y2-2x=0和圆O2:x2+y2-4y=0的位置关系是
(A)相离 (B)相交 (C)外切 (D)内切
解: 化成标准方程: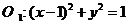 ,
,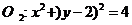 ,则
,则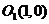 ,
,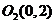 ,
,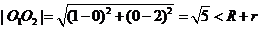 ,两圆相交
,两圆相交
32.(重庆卷文3)曲线C: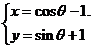 (
(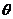 为参数)的普通方程为
为参数)的普通方程为
(A)(x-1)2+(y+1)2=1 (B) (x+1)2+(y+1)2=1
(C) (x-1)2+(y-1)2=1 (D) (x-1)2+(y-1)2=1
[答案]C
[解析]本小题主要考查圆的参数方程。移项,平方相加,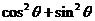
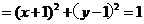 ,故选C。
,故选C。
33.(四川延考理9)过点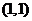 的直线与圆
的直线与圆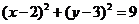 相交于
相交于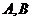 两点,则
两点,则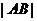 的最小值为
的最小值为
(A)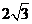 (B)
(B)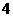 (C)
(C)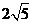 (D)
(D)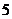
解: 弦心距最大为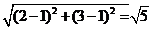 ,
,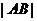 的最小值为
的最小值为
34.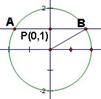 (四川延考文9)过点
(四川延考文9)过点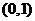 的直线与圆
的直线与圆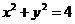 相交于
相交于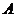 ,
,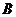 两点,则
两点,则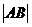 的最小值为( )
的最小值为( )
A.2 B.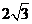 C.3 D.
C.3 D.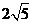
解:如图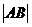 最小时,弦心距最大为1,
最小时,弦心距最大为1,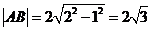
(2009江苏卷18)(本小题满分16分) 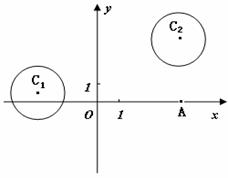 在平面直角坐标系
在平面直角坐标系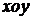 中,已知圆
中,已知圆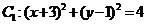 和圆
和圆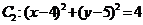 .(1)若直线
.(1)若直线 过点
过点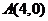 ,且被圆
,且被圆 截得的弦长为
截得的弦长为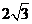 ,求直线
,求直线 的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线
的方程;(2)设P为平面上的点,满足:存在过点P的无穷多对互相垂直的直线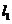 和
和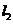 ,它们分别与圆
,它们分别与圆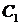 和圆
和圆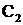 相交,且直线
相交,且直线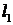 被圆
被圆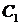 截得的弦长与直线
截得的弦长与直线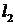 被圆
被圆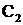 截得的弦长相等,试求所有满足条件的点P的坐标。
截得的弦长相等,试求所有满足条件的点P的坐标。
解 (1)设直线 的方程为:
的方程为: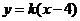 ,即
,即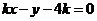
由垂径定理,得:圆心 到直线
到直线 的距离
的距离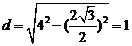 ,
,
结合点到直线距离公式,得: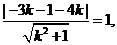
 化简得:
化简得: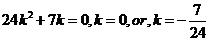
求直线 的方程为:
的方程为: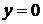 或
或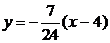 ,即
,即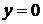 或
或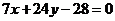
(2) 设点P坐标为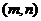 ,直线
,直线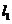 、
、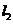 的方程分别为:
的方程分别为: 

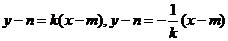 ,即:
,即: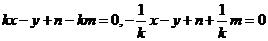
因为直线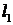 被圆
被圆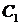 截得的弦长与直线
截得的弦长与直线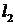 被圆
被圆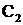 截得的弦长相等,两圆半径相等。
截得的弦长相等,两圆半径相等。
由垂径定理,得::圆心 到直线
到直线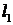 与
与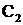 直线
直线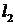 的距离相等。
的距离相等。 
故有: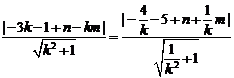 ,
,
化简得: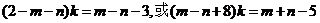
关于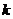 的方程有无穷多解,有:
的方程有无穷多解,有: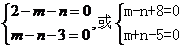



解之得:点P坐标为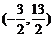 或
或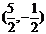 。
。
2008高考试题及解析
14.(2009上海卷文) 已知实数x、y满足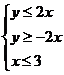 则目标函数z=x-2y的最小值是_______.
则目标函数z=x-2y的最小值是_______.
答案 -9
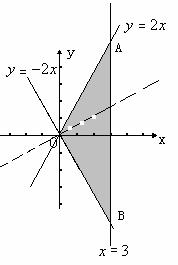
解析 画出满足不等式组的可行域如右图,目标函数化为: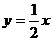 -z,画直线
-z,画直线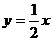 及其平行线,当此直线经过点A时,-z的值最大,z的值最小,A点坐标为(3,6),所以,z的最小值为:3-2×6=-9。
及其平行线,当此直线经过点A时,-z的值最大,z的值最小,A点坐标为(3,6),所以,z的最小值为:3-2×6=-9。
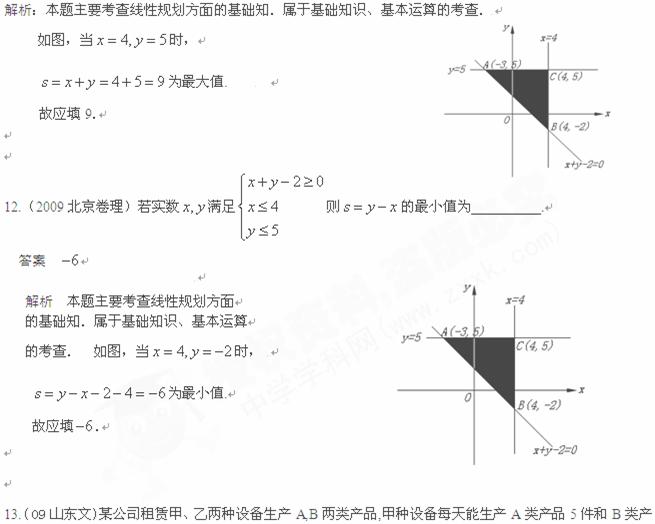
11.(2009北京文)若实数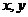 满足
满足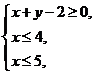 则
则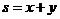 的最大值为
.
的最大值为
.
答案 9
 品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为___元.
品10件,乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元,设备乙每天的租赁费为300元,现该公司至少要生产A类产品50件,B类产品140件,所需租赁费最少为___元.


解析 设甲种设备需要生产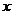 天, 乙种设备需要生产
天, 乙种设备需要生产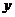 天, 该公司所需租赁费为
天, 该公司所需租赁费为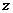 元,则
元,则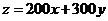 ,甲、乙两种设备生产A,B两类产品的情况为下表所示:
,甲、乙两种设备生产A,B两类产品的情况为下表所示:
 产品 产品 设备 |
A类产品 (件)(≥50) |
B类产品 (件)(≥140) |
租赁费 (元) |
|
甲设备 |
5
|
10 |
200 |
|
乙设备 |
6
|
20
|
300 |
则满足的关系为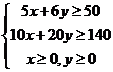 即:
即: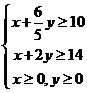 ,
,


作出不等式表示的平面区域,当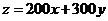 对应的直线过两直线
对应的直线过两直线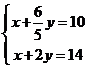 的交点(4,5)时,目标函数
的交点(4,5)时,目标函数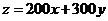 取得最低为2300元.
取得最低为2300元. 

10.(2009浙江卷文)若实数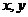 满足不等式组
满足不等式组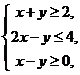 则
则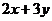 的最小是
.
的最小是
.
[命题意图]此题主要是考查了线性规划中的最值问题,此题的考查既体现了正确画线性区域的要求,也体现了线性目标函数最值求解的要求
解析 通过画出其线性规划,可知直线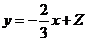 过点
过点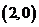 时,
时,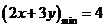
9.(2009浙江理)若实数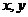 满足不等式组
满足不等式组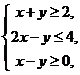 则
则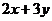 的最小值是 . 答案 4
的最小值是 . 答案 4
解析 通过画出其线性规划,可知直线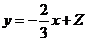 过点
过点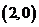 时,
时,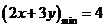
7.(湖北文14)过原点O作圆x2+y2‑-6x-8y+20=0的两条切线,设切点分别为P、Q,
则线段PQ的长为 。[答案]4
[解析]可得圆方程是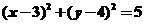 又由圆的切线性质及在三角形中运用正弦定理得
又由圆的切线性质及在三角形中运用正弦定理得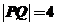 .
.
8(江西理16).设直线系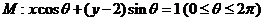 ,对于下列四个命题:
,对于下列四个命题:
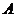 .
.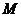 中所有直线均经过一个定点
中所有直线均经过一个定点
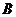 .存在定点
.存在定点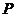 不在
不在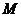 中的任一条直线上
中的任一条直线上
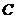 .对于任意整数
.对于任意整数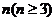 ,存在正
,存在正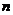 边形,其所有边均在
边形,其所有边均在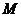 中的直线上
中的直线上
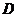 .
.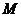 中的直线所能围成的正三角形面积都相等其中真命题的代号是 (写出所有真命题的代号).
中的直线所能围成的正三角形面积都相等其中真命题的代号是 (写出所有真命题的代号).
[解析]因为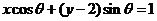 所以点
所以点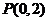 到
到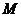 中每条直线的距离
中每条直线的距离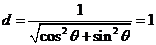
即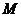 为圆
为圆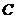 :
: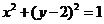 的全体切线组成的集合,从而
的全体切线组成的集合,从而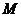 中存在两条平行直线,所以A错误;
中存在两条平行直线,所以A错误;
又因为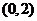 点不存在任何直线上,所以B正确;对任意
点不存在任何直线上,所以B正确;对任意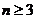 ,存在正
,存在正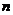 边形使其内切圆为圆
边形使其内切圆为圆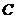 ,故
,故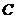 正确;
正确;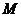 中边能组成两个大小不同的正三角形
中边能组成两个大小不同的正三角形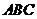 和
和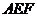 ,故D错误,故命题中正确的序号是
B,C.[答案]
,故D错误,故命题中正确的序号是
B,C.[答案]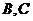
6.(全国Ⅱ文15)已知圆O: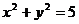 和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 [答案]
和点A(1,2),则过A且与圆O相切的直线与两坐标轴围成的三角形的面积等于 [答案] 
[解析]由题意可直接求出切线方程为y-2=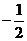 (x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和
(x-1),即x+2y-5=0,从而求出在两坐标轴上的截距分别是5和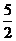 ,所以所求面积为
,所以所求面积为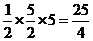 。
。
 的倾斜角可以是
的倾斜角可以是
①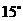 ②
②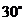 ③
③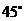 ④
④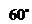 ⑤
⑤

其中正确答案的序号是 .(写出所有正确答案的序号)
[解析]解:两平行线间的距离为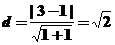 ,由图知直线
,由图知直线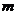 与
与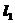 的夹角为
的夹角为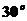 ,
,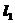 的倾斜角为
的倾斜角为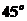 ,所以直线
,所以直线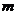 的倾斜角等于
的倾斜角等于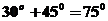 或
或 。
。
[答案]①⑤
5.(全国Ⅱ理16)已知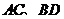 为圆
为圆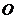 :
: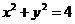 的两条相互垂直的弦,垂足为
的两条相互垂直的弦,垂足为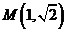 ,则四边形
,则四边形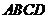 的面积的最大值为
。[答案]5
的面积的最大值为
。[答案]5
[解析]设圆心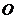 到
到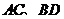 的距离分别为
的距离分别为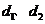 ,则
,则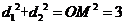 .
.
四边形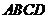 的面积
的面积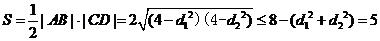
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com