
10.(全国I文6)下面给出四个点中,位于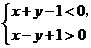 表示的平面区域内的点是( )
表示的平面区域内的点是( )
A.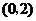 B.
B. C.
C.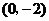 D.
D.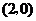
解:将四个点的坐标分别代入不等式组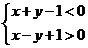 ,满足条件的是
,满足条件的是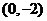 ,选C。
,选C。
9.(全国I理6)下面给出的四个点中,到直线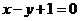 的距离为
的距离为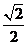 ,且位于
,且位于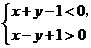 表示的平面区域内的点是( )
表示的平面区域内的点是( )
A.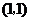 B.
B.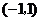 C.
C.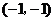 D.
D.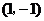
解:给出的四个点中,到直线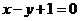 的距离都为
的距离都为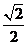 ,位于
,位于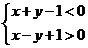
表示的平面区域内的点是(-1,-1),∵  ,选C。
,选C。
7.(江苏卷10)在平面直角坐标系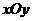 中,已知平面区域
中,已知平面区域 ,则平面区域
,则平面区域 时取最大值6,当(x,y)=(
时取最大值6,当(x,y)=( )时取最小值
)时取最小值 ,选A.
,选A.
6. (湖北文8)由直线
(湖北文8)由直线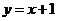 上的一点向圆
上的一点向圆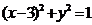 引切线,则切线长的最小值为
引切线,则切线长的最小值为
A.1 B.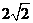 C.
C.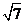 D.
D.
答案:选C
解析:切线长的最小值是当直线y=x+1上的点与圆心距离最小时取得,圆心(3,0)到直线的距离为
d=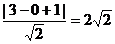 ,圆的半径为1,故切线长的最小值为
,圆的半径为1,故切线长的最小值为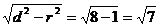 ,选C
,选C
5.(湖北理10)已知直线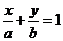 (
( 是非零常数)与圆
是非零常数)与圆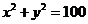 有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )
A.60条 B.66条 C.72条 D.78条
答案:选A
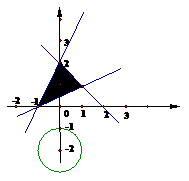
4.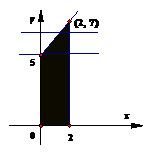 (北京文6)若不等式组
(北京文6)若不等式组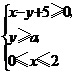 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则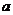 的取值范围是( )
的取值范围是( )
A.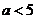 B.
B. C.
C.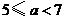 D.
D.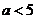 或
或
解:如图,不等式组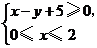 表示的平面区域是一个梯形,
表示的平面区域是一个梯形,
它的一个顶点坐标是(2,7),用平行于x轴的直线y≥a截
梯形得到三角形,则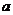 的取值范围是
的取值范围是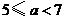 ,选C。
,选C。
3.(北京理6)若不等式组 表示的平面区域是一个三角形,则
表示的平面区域是一个三角形,则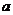 的取值范围是
的取值范围是
A. B.
B.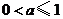 C.
C.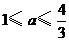 D.
D.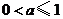 或
或
 解:不等式组
解:不等式组 ,将前三个不等式画出可行域,
,将前三个不等式画出可行域,
三个顶点分别为(0,0),(1,0),( ,
, ),第四个
),第四个
不等式 ,表示的是斜率为-1的直线的下方,
,表示的是斜率为-1的直线的下方,
∴ 当0<a≤1时,表示的平面区域是一个三角形,
当a≥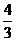 时,表示的平面区域也是一个三角形,选D。
时,表示的平面区域也是一个三角形,选D。
2.(安徽文5)若圆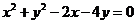 的圆心到直线
的圆心到直线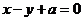 的距离为
的距离为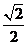 ,则
,则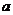 的值为( )
的值为( )
A. 或
或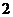 B.
B.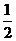 或
或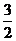 C.
C.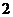 或
或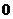 D.
D. 或
或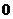
[答案] C
[解析]若圆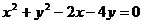 的圆心(1,2)到直线
的圆心(1,2)到直线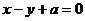 的距离为
的距离为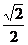 ,
,
∴ 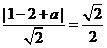 ,∴ a=2或0,选C。
,∴ a=2或0,选C。
1.(安徽理7)如果点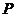 在平面区域
在平面区域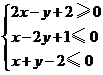 上,点
上,点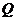 在曲线
在曲线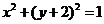 上,那么
上,那么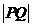 的最小值为( )
的最小值为( )
 A.
A.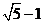 B.
B.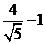 C.
C.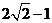 D.
D.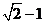
[答案] A
[解析]点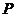 在平面区域
在平面区域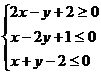 上,画出可行域如图,
上,画出可行域如图,
点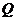 在圆
在圆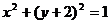 上,那么
上,那么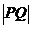 的最小值为圆心
的最小值为圆心
(0,-2)到直线x-2y+1=0的距离减去半径1,即为 -1,选A。
-1,选A。
(三)解答题
1.(海南宁夏卷理22文22)如图,过圆O外一点M作它的一条切线,切点为A,过A作直线AP垂直直线OM,垂足为P。
 (1)证明:OM·OP = OA2;
(1)证明:OM·OP = OA2;
(2)N为线段AP上一点,直线NB垂直直线ON,
且交圆O于B点。过B点的切线交直线ON于K。
证明:∠OKM = 90°。
解:(Ⅰ)证明:因为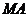 是圆
是圆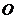 的切线,所以
的切线,所以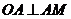 .
.
又因为 .在
.在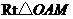 中,由射影定理知,
中,由射影定理知,
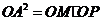 .
.
(Ⅱ)证明:因为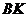 是圆
是圆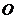 的切线,
的切线,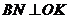 .同(Ⅰ),有
.同(Ⅰ),有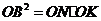 ,又
,又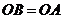 ,
,
所以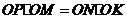 ,即
,即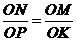 .又
.又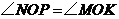 ,
,
所以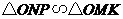 ,故
,故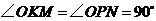 .
.
2.(海南宁夏卷文20)已知m∈R,直线l: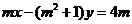 和圆C:
和圆C: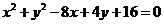 。
。
(1)求直线l斜率的取值范围;(2)直线l能否将圆C分割成弧长的比值为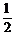 的两段圆弧?为什么?
的两段圆弧?为什么?
[试题解析](1)直线 的方程可化为
的方程可化为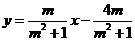 ,此时斜率
,此时斜率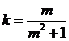
因为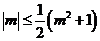 ,所以
,所以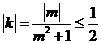 ,当且仅当
,当且仅当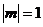 时等号成立所以,斜率k的取值范围是
时等号成立所以,斜率k的取值范围是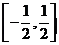 ;
;
(2)不能.由(1知 的方程为
的方程为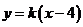 ,其中
,其中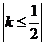 ;
;
圆C的圆心为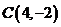 ,半径
,半径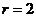 ;圆心C到直线
;圆心C到直线 的距离
的距离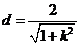
由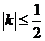 ,得
,得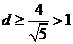 ,即
,即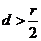 ,从而,若
,从而,若 与圆C相交,则圆C截直线
与圆C相交,则圆C截直线 所得
所得
的弦所对的圆心角小于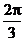 ,所以
,所以 不能将圆C分割成弧长的比值为
不能将圆C分割成弧长的比值为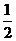 的两端弧;
的两端弧;
[高考考点]直线与圆及不等式知识的综合应用
[易错点]:对有关公式掌握不到位而出错。
[全品备考提示]:本题不是很难,但需要大家有扎实的功底,对相关知识都要受熟练掌握;
3.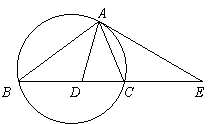 (江苏卷21A)如图,设△ABC的外接圆的切线AE与
(江苏卷21A)如图,设△ABC的外接圆的切线AE与
BC的延长线交于点E,∠BAC的平分线与BC交于点D.
求证: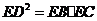 .
.
证明:如图,因为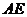 是圆的切线, 所以,
是圆的切线, 所以,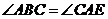 ,
,
又因为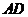 是
是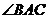 的平分线, 所以
的平分线, 所以 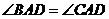
从而 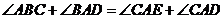 因为
因为 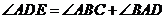 ,
,
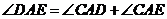 所以
所以 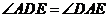 ,故
,故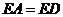 .
.
因为 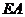 是圆的切线,所以由切割线定理知,
是圆的切线,所以由切割线定理知, 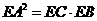 , 而
, 而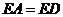 ,所以
,所以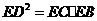
2007高考试题及解析
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com