
7.正三棱锥侧棱长与底面边长的比值的取值范围是
A.[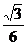 ,+∞) B.[
,+∞) B.[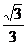 ,+∞)
,+∞)
C.(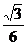 ,+∞) D.(
,+∞) D.(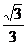 ,+∞)
,+∞)
6.曲线y=2x4上的点到直线y=-x-1的距离的最小值为
A.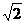 B.
B.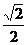 C.
C.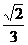 D.
D.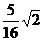
5.设Sn是等差数列{an}的前n项和,若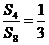 ,则
,则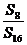 等于
等于
A.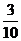 B.
B.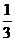 C.
C.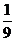 D.
D.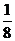
4.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的两倍,则m的值为
A.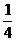 B.
B.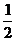 C.2 D.4
C.2 D.4
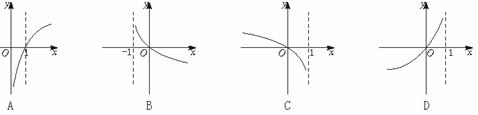
3.函数y=log2(1-x)的图象是
2.设集合M={x|x2-x<0,x∈R},N={x||x|<2,x∈R},则
A.N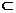 M B.M∩N=M
M B.M∩N=M
C.M∪N=M D.M∪N=R
1.设M和m分别表示函数y=2sinx-1的最大值和最小值,则M+m等于
A.1 B.2 C.-2 D.-1
22、 设双曲线C: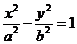 (a>0,b>0)的离心率为e,若直线l: x=
(a>0,b>0)的离心率为e,若直线l: x=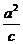 与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
与两条渐近线相交于P、Q两点,F为右焦点,△FPQ为等边三角形.
(1)求双曲线C的离心率e的值;
(2)若双曲线C被直线y=ax+b截得的弦长为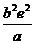 ,求双曲线c的方程.
,求双曲线c的方程.
高二年级数学试题月二(理)答案
1-12题 ABCB CDCC CCBA
(13)2:3:(-4)
(14)4ab=1 (15)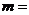 15
15 
 (16)
(16)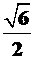
17解:由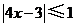 ,得
,得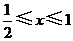 ,www.k@s@5@
高#考#资#源#网
,www.k@s@5@
高#考#资#源#网
因此,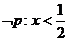 或
或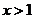 ,
,
由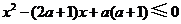 ,得
,得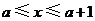 .
.
因此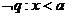 或
或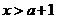 ,
,
因为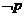 是
是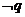 的必要条件
的必要条件
所以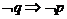 ,即
,即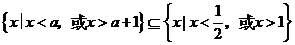 .
.
如下图所示:
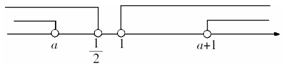
因此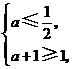 解得
解得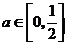 .。。。。。。。。。。。。。。。。。。10分
.。。。。。。。。。。。。。。。。。。10分
18解:若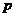 是真命题,则
是真命题,则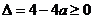 所以
所以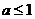
若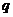 是真命题,则
是真命题,则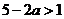 所以
所以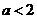 。。。。。。。4分
。。。。。。。4分
因为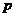 或
或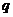 为真命题,
为真命题,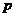 且
且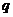 为假命题
为假命题
所以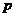 为真命题
为真命题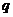 为假命题或
为假命题或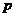 为假命题
为假命题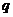 为真命题。。。6分
为真命题。。。6分
即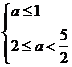 或
或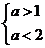 。。。。。。。。。。。。。。。。10分
。。。。。。。。。。。。。。。。10分
所以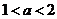 。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
。。。。。。。。。。。。。。。。。。。。。。。。。。。。。。12分
19解以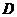 为原点,
为原点,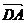 、
、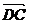 、
、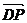 分别为
分别为
(Ⅰ)以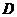 为原点,
为原点,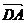 、
、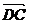 、
、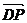 分别为
分别为
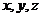 轴建立空间直角坐标系.
轴建立空间直角坐标系.
由已知可得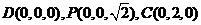 设
设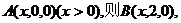
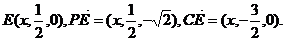 由
由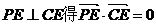 ,
,
即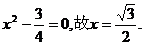 由
由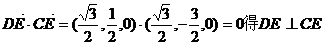 ,
,
又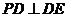 ,故
,故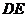 是异面直线
是异面直线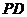 与
与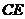 的公垂线,易得
的公垂线,易得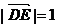 ,故异面直线
,故异面直线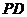 ,
,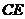 的距离为
的距离为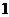 .
.
(Ⅱ)作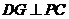 ,可设
,可设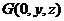 .由
.由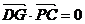 得
得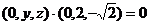
即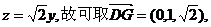 作
作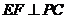 于
于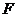 ,设
,设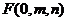 ,
,
则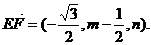 www.k@s@5@
高#考#资#源#网
www.k@s@5@
高#考#资#源#网
由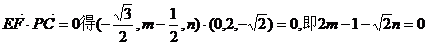 ,
,
又由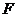 在
在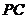 上得
上得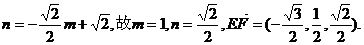
因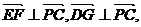 故
故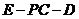 的平面角
的平面角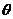 的大小为向量
的大小为向量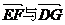 的夹角.
的夹角.
20解:(1)设椭圆方程为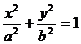
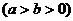 ,则
,则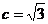 ,
,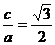 ,
,
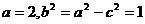 ……2分
……2分
∴ 所求椭圆方程为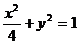 ……4分
……4分
(2)由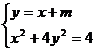 ,消去y,得
,消去y,得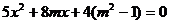 ,
,
则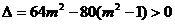 得
得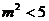 (*)……6分
(*)……6分
设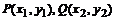 ,
,
则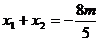 ,
,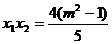 ,
,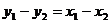 ,……8分
,……8分
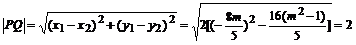 ……10分
……10分
解得.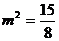 ,满足(*) ∴
,满足(*) ∴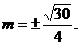 ……12分
……12分
21解:(Ⅰ)建立如图所示的空间直角坐标系,
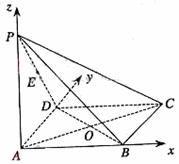 则
则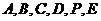 的坐标为
的坐标为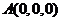 、
、
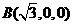 、
、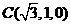 、
、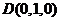 、
、
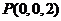 、
、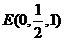 ,
,
从而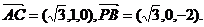
设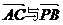 的夹角为
的夹角为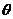 ,则
,则
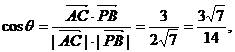
∴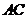 与
与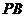 所成角的余弦值为
所成角的余弦值为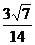 .。。。。。。。。。。。。。。。。。。。6分
.。。。。。。。。。。。。。。。。。。。6分
(Ⅱ)由于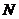 点在侧面
点在侧面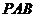 内,故可设
内,故可设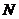 点坐标为
点坐标为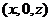 ,则
,则
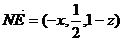 ,由
,由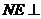 面
面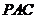 可得,
可得,
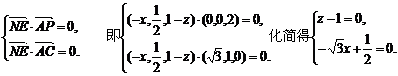 ∴
∴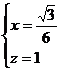
即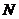 点的坐标为
点的坐标为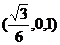 ,从而
,从而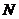 点到
点到 和
和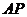 的距离分别为
的距离分别为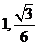 .。。。12分
.。。。12分
22解析:(1)双曲线C的右准线l的方程为:x=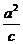 ,两条渐近线方程为:
,两条渐近线方程为: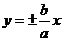 .
.
 ∴ 两交点坐标为
∴ 两交点坐标为 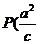 ,
,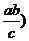 、
、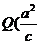 ,
,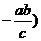 .
.
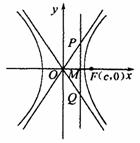
∵ △PFQ为等边三角形,则有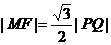 (如图).
(如图).
∴ 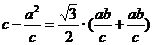 ,即
,即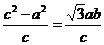 .
.
解得 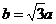 ,c=2a.∴
,c=2a.∴ 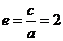 .……………………………………6分
.……………………………………6分
(2)由(1)得双曲线C的方程为把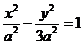 .www.k@s@5@
高#考#资#源#网
.www.k@s@5@
高#考#资#源#网
把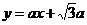 代入得
代入得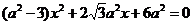 .
.
依题意 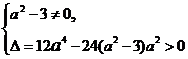 ∴
∴ 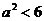 ,且
,且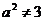 .
.
∴ 双曲线C被直线y=ax+b截得的弦长为
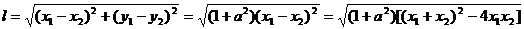
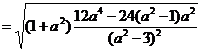
∵ 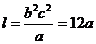 . ∴
. ∴ 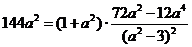 .
.
整理得 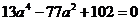 .
.
∴ 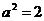 或
或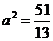 .
.
∴ 双曲线C的方程为: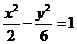 或
或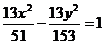 .…………………12分
.…………………12分
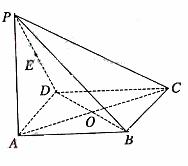
21、如图,在四棱锥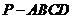 中,底面
中,底面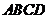 为矩形,侧棱
为矩形,侧棱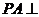 底面
底面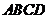 ,
,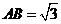 ,
,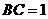 ,
,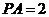 ,
, 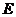 为
为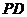 的中点.(Ⅰ)求直线
的中点.(Ⅰ)求直线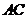 与
与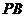 所成角的余弦值;(Ⅱ)在侧面
所成角的余弦值;(Ⅱ)在侧面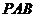 内找一点
内找一点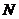 ,使
,使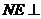 面
面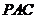 ,并求出点
,并求出点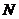 到
到 和
和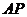 的距离.
的距离.
20、已知椭圆的两焦点为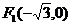 ,
,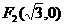 ,离心率
,离心率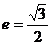 .(1)求此椭圆的方程;(2)设直线
.(1)求此椭圆的方程;(2)设直线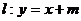 ,若
,若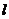 与此椭圆相交于
与此椭圆相交于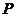 ,
,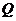 两点,且
两点,且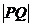 等于椭圆的短轴长,求
等于椭圆的短轴长,求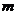 的值;
的值;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com