
2、例2(2006年福建卷)如图,四面体ABCD中,O、E分别是BD、BC的中点,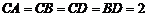
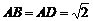
(I)求证: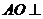 平面BCD;
平面BCD;
(II)求异面直线AB与CD所成角的大小;
(III)求点E到平面ACD的距离。

解:(I)略
(II)解:以O为原点,如图建立空间直角坐标系,
则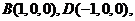
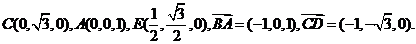
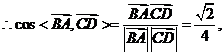
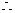 异面直线AB与CD所成角的大小为
异面直线AB与CD所成角的大小为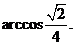
(III)解:设平面ACD的法向量为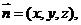 则
则
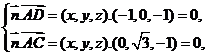
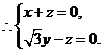
令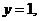 得
得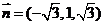 是平面ACD的一个法向量,又
是平面ACD的一个法向量,又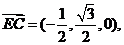
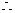 点E到平面ACD的距离
点E到平面ACD的距离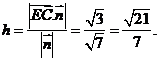
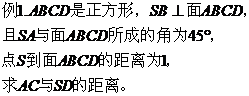
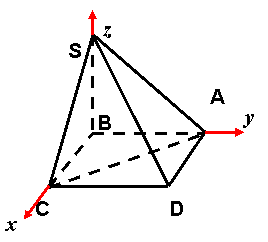
 例2、已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。
例2、已知正方形ABCD的边长为4,CG⊥平面ABCD,CG=2,E、F分别是AB、AD的中点,求点B到平面GEF的距离。
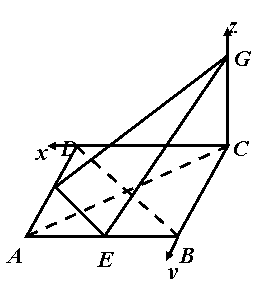
例3、在边长为1的正方体ABCD-A1B1C1D1中,M、N、E、F分别是棱A1B1、A1D1、B1C1、C1D1的中点,求平面AMN与平面EFDB的距离。
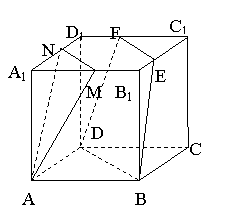
1、例1 直三棱柱ABC-A1B1C1的侧棱AA1=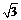 ,底面ΔABC中,∠C=90°,AC=BC=1,求点B1到平面A1BC的距离。
,底面ΔABC中,∠C=90°,AC=BC=1,求点B1到平面A1BC的距离。
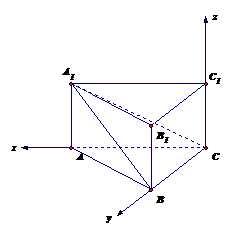
解1:如图建立空间直角坐标系,由已知得直棱柱各顶点坐标如下:
A(1,0,0),B(0,1,0),C(0,0,0)A1(1,0,),B1(0,1,),C1(0,0,)
∴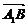 =(-1,1,-),
=(-1,1,-),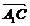 =(-1,0,-)
=(-1,0,-)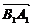 =(1,-1,0)
=(1,-1,0)
设平面A1BC的一个法向量为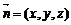 ,则
,则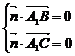
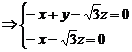
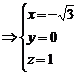
即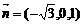
所以,点B1到平面A1BC的距离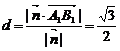
解2 建系设点同上(略),设平面A1BC的方程为ax+by+cz+d=0
(a,b,c,d不全为零),把点A1,B,C三点坐标分别代入平面方程得
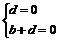
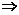
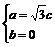
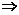 平面A1BC的方程为x+z=0
平面A1BC的方程为x+z=0
又 B1(0,1,)
设点B1到平面A1BC的距离为d,则
d= =
4、向量法在求点到平面的距离中
(1)设分别以平面外一点P与平面内一点M为起点和终点的向量为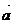 ,平面的法向量为
,平面的法向量为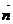 ,则P到平面的距离d等于
,则P到平面的距离d等于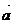 在
在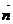 方向上正射影向量的模。
方向上正射影向量的模。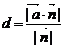
(2)先求出平面的方程,然后用点到平面的距离公式:点P(x0,y0,z0)到平面AX+BY+CZ+D=0的距离d为:d=
2、向量法在求异面直线间的距离
设分别以这两异面直线上任意两点为起点和终点的向量为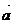 ,与这两条异面直线都垂直的向量为
,与这两条异面直线都垂直的向量为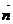 ,则两异面直线间的距离是
,则两异面直线间的距离是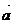 在
在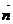 方向上的正射影向量的模。
方向上的正射影向量的模。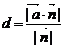
1、两点间的距离公式
设空间两点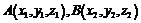 ,则
,则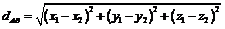
3、求空间中的距离有⑴直接法,即直接求出垂线段的长度;⑵转化法,转化为线面距或面面距,或转化为某三棱锥的高,由等积法或等面积法求解;⑶向量法求解。
2、距离的特征:⑴距离是指相应线段的长度;⑵此线段是所有相关线段中最短的;⑶除两点间的距离外,其余总与垂直相联系。
1、空间中的距离包括:两点间的距离,点到直线的距离,点到平面的距离,平行直线间的距离,异面直线直线间的距离,直线与平面的距离,两个平行平面间的距离。这些距离的定义各不相同,但都是转化为平面上两点间的距离来计算的。
8、平行六面体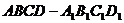 中,
中,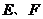 分别是
分别是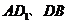 的中点,用向量方法证明:
的中点,用向量方法证明:
(1)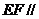 平面
平面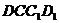 ;(2)
;(2)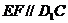 。
。
答案见《突破课堂》P64巩固练习12
7、正方体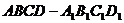 中,
中,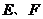 分别是
分别是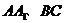 中点,求证:平面
中点,求证:平面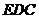
 平面
平面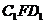 。
。
答案见《突破课堂》P62巩固练习9
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com