
18、解: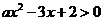 的解集为
的解集为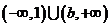 根据不等式解集的意义可知,方程
根据不等式解集的意义可知,方程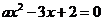 的两根为
的两根为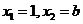 由韦达定理得
由韦达定理得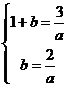 解之得
解之得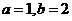
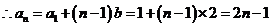 ……………………………………6分
……………………………………6分
(2)由(1)得: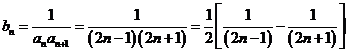
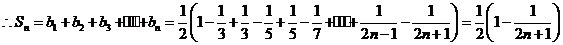
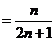 …………………………………………………………………………12分
…………………………………………………………………………12分
17.解:设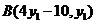 ,由AB中点在
,由AB中点在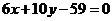 上,
上,
可得: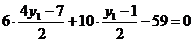 ,y1 = 5,所以
,y1 = 5,所以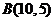 .………………5分
.………………5分
设A点关于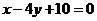 的对称点为
的对称点为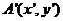 ,
,
则有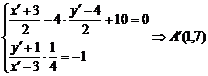 .故
.故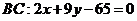 .………………10分
.………………10分
22.(本小题满分12分)
设数列 的前
的前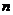 项和为
项和为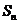 ,且
,且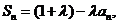 其中
其中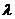 为常数,且
为常数,且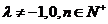
(1)证明:数列 是等比数列。
是等比数列。
(2)设数列 的公比
的公比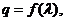 数列
数列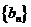 满足
满足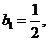
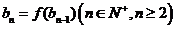 ,求数列
,求数列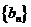 的通项公式。
的通项公式。
(3)设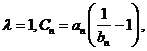 数列
数列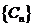 的前
的前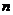 项和为
项和为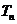 ,求证:当
,求证:当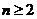 时,
时,
楠杆高中2009-2010学年上期高三第二次月考答案
21.(本小题满分12分)
已知函数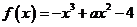
(1)若 在
在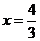 处取得极值,求函数
处取得极值,求函数 的单调区间。
的单调区间。
(2)若存在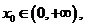 时,使得不等式
时,使得不等式 成立,求实数
成立,求实数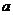 的取值范围。
的取值范围。
20.(本小题满分12分)
设命题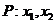 是方程
是方程 的两个实根,不等式
的两个实根,不等式
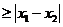 对任意实数
对任意实数 恒成立, 命题
恒成立, 命题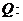 函数
函数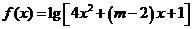 的值域为全体实数,若
的值域为全体实数,若 且
且 为真,试求实数
为真,试求实数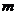 的取值范围
的取值范围
19.(本小题满分12分)
已知 的面积
的面积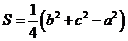 其中
其中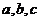 分别为角
分别为角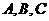 所对的边
所对的边
(1)求角 的大小。
的大小。
(2)若 ,求
,求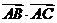 的最大值。
的最大值。
18.(本小题满分12分)
已知等差数列 的首项为
的首项为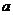 ,公差为
,公差为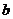 ,且不等式
,且不等式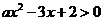 的解集为
的解集为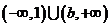
(1)求数列 的通项公式
的通项公式
(2)设数列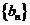 满足
满足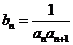 求数列
求数列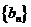 的前
的前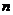 项和
项和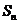 。
。
17.(本小题满分10分)已知 的顶点A为(3,-1),AB边上的中线所在直线方程为
的顶点A为(3,-1),AB边上的中线所在直线方程为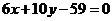 ,
,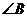 的平分线所在直线方程为
的平分线所在直线方程为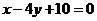 ,求BC边所在直线的方程.
,求BC边所在直线的方程.
16、定义在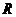 上的偶函数
上的偶函数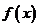 ,满足
,满足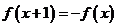 且
且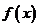 在
在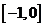 上是增函数,有下列五个关于
上是增函数,有下列五个关于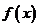 的命题:①
的命题:①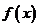 是周期函数,②
是周期函数,②
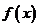 的图象关于
的图象关于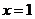 对称 ③
对称 ③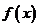 在
在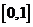 上是增函数 ④
上是增函数 ④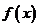 在
在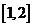 是减函数 ⑤
是减函数 ⑤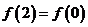
其中正确的命题的序号是______________(写出所有正确命题的序号)
15、若以曲线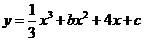 (
(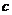 为常数)上任意一点为切点的切线斜率恒为非负数,则实数
为常数)上任意一点为切点的切线斜率恒为非负数,则实数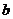 的取值范围为_________________。
的取值范围为_________________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com