8．分子式为的同分异构体共有(不考虑立体异构)

　 A．3种　　 B．4种　　 C．5种D．6种

7．下列各项表达中正确的是

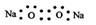A．的电子式为

B．的乙醇和丙醇混合液完全燃烧生成的为 (标准状况)

C．在氮原子中，质子数为7而中子数不一定为7

D. 的结构示意图为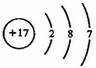

6．在白花豌豆品种栽培园中，偶然发现了一株开红花的豌豆植株，推测该红花表现型的出现是花色基因突变的结果。为了确定该推测是否正确，应检测和比较红花植株与白花植株中

　 A．花色基因的碱基组成　　 B．花色基因的序列

　 C．细胞的含量　　　 D．细胞的含量

5．将神经细胞置于相当于细胞外液的溶液(溶液)中，可测得静息电位。给予细胞一个适宜的刺激，膜两侧出现一个暂时性的电位变化，这种膜电位变化称为动作电位。适当降低溶液中的浓度，测量该细胞的静息电位和动作电位，可观察到

　 A．静息电位值减小　 　　B．静息电位值增大

　 C．动作电位峰值升高　　 D．动作电位峰值降低

4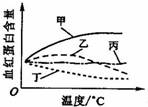．水中氧含量随水温的升高而下降。生活在寒温带湖泊中的某动物，其血液中的血红蛋白含量与其生活的水温有关。右图中能正确表示一定温度范围内该动物血液中血红蛋白含量随水温变化趋势的曲线是

　 A．甲　　 B．乙

　 C．丙　　 D．丁

3．若要在普通显微镜下观察到质壁分离、和脂肪，下列四组材料中应选择的一组是

　 A．水稻胚乳和花生子叶　　 B．天竺葵叶和水稻胚乳

　 C．紫色洋葱和花生子叶　　 D．天竺葵叶和紫色洋葱

2．下列关于呼吸作用的叙述，正确的是

　 A．无氧呼吸的终产物是丙酮酸

　 B．有氧呼吸产生的在线粒体基质中与氧结合生成水

　 C．无氧呼吸不需要的参与。该过程最终有的积累

　 D．质量相同时，脂肪比糖原有氧氧化释放的能量多

　　 一项是符合题目要求的。

1．下列有关细胞的叙述，正确的是

　 A．病毒是一类具有细胞结构的生物

　 B．蓝藻细胞具有细胞核且DNA分子呈环状

　 C．人体所有细胞的细胞周期持续时间相同

　 D．内质网膜和高尔基体膜都具有流动性

(13)设为区间上的连续函数，且恒有，可以用随机模拟方法近似计算积分，先产生两组(每组N个)区间上的均匀随机数和，由此得到N个点，再数出其中满足的点数，那么由随机模拟方案可得积分的近似值为 　　　。

(14)正视图为一个三角形的几何体可以是______(写出三种)

(15)过点A(4,1)的圆C与直线x-y=0相切于点B(2,1)，则圆C的方程为____

(16)在△ABC中，D为边BC上一点，BD=DC，ADB=120°，AD=2，若△ADC的面积为，则BAC=_______

三，解答题：解答应写出文字说明，正明过程和演算步骤

(17)(本小题满分12分)

设数列满足

(1)　　　 求数列的通项公式；

(2)　　　 令，求数列的前n项和

(18)(本小题满分12分)

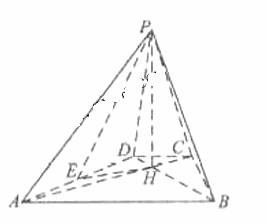
如图，已知四棱锥P-ABCD的底面为等腰梯形，ABCD,ACBD，垂足为H，PH是四棱锥的高 ，E为AD中点

(1)　　　 证明：PEBC

(2)　　　 若APB=ADB=60°，求直线PA与平面PEH所成角的正弦值

(19)(本小题12分)

为调查某地区老人是否需要志愿者提供帮助，用简单随机抽样方法从该地区调查了500位老年人，结果如下：

(1)　　　 估计该地区老年人中，需要志愿者提供帮助的老年人的比例；

(2)　　　 能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关？

(3)　　　 根据(2)的结论，能否提供更好的调查方法来估计该地区老年人，需要志愿帮助的老年人的比例？说明理由

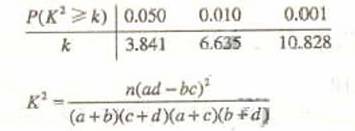附：

(20)(本小题满分12分)

设分别是椭圆的左、右焦点，过斜率为1的直线与相交于两点，且成等差数列。

(1)求的离心率；

　(2) 设点满足，求的方程

(21)(本小题满分12分)

设函数。

(1)　　　 若，求的单调区间；

(2)　　　 若当时，求的取值范围

请考生在第(22)、(23)、(24)三题中任选一题作答，如果多做，则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目的题号涂黑。

(22)(本小题满分10分)选修4-1：几何证明选讲

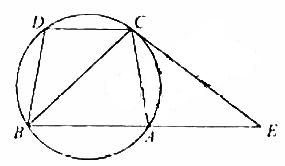
　　　 如图，已经圆上的弧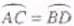，过C点的圆切线与BA的延长线交于E点，证明：

(Ⅰ)∠ACE=∠BCD；

(Ⅱ)BC²=BF×CD。

(23)(本小题满分10分)选修4-4：坐标系与参数方程

　　　 已知直线C₁(t为参数)，C₂(为参数)，

(Ⅰ)当=时，求C₁与C₂的交点坐标；

(Ⅱ)过坐标原点O做C₁的垂线，垂足为，P为OA中点，当变化时，求P点的轨迹的参数方程，并指出它是什么曲线。

(24)(本小题满分10分)选修4-5，不等式选项

　　　 设函数

(Ⅰ)画出函数的图像

(Ⅱ)若不等式≤的解集非空，求a的取值范围。

2010年普通高等学校招生全国统一考试

(1)已知集合},,则

(A)(0,2)　　　　　 (B)[0,2]　　　　 (C){0,2]　　　　　 (D){0,1,2}

(2)已知复数，是z的共轭复数，则=

A. 　　　　　B.　　　　 C.1　　　　　　　 D.2

(3)曲线在点(-1，-1)处的切线方程为

(A)y=2x+1　　　　　 (B)y=2x-1　　 C y=-2x-3　　　 D.y=-2x-2

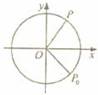
(4)如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P₀(，-)，角速度为1，那么点P到x轴距离d关于时间t的函数图像大致为

(5)已知命题

：函数在R为增函数，

：函数在R为减函数，

则在命题：，：，：和：中，真命题是

(A)，　　 (B)，　　 (C)，　　　 (D)，

(6)某种种子每粒发芽的概率都为0.9，现播种了1000粒，对于没有发芽的种子，每粒需再补种2粒，补种的种子数记为X，则X的数学期望为

(A)100　　　 (B)200　　　 (C)300　　　　 (D)400

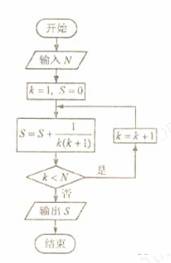
(7)如果执行右面的框图，输入，则输出的数等于

(A)

(B)

(C)

(D)

(8)设偶函数满足，则

(A) 　　　　　　　　　　　　　　 (B)

(C) 　　　　　　　　　　　　　　　　 (D)

(9)若，是第三象限的角，则

(A) 　　 (B) 　　　　 (C) 2　　　 (D) -2

(10)设三棱柱的侧棱垂直于底面，所有棱长都为，顶点都在一个球面上，则该球的表面积为

(A) 　　　　　 (B) 　　　　　　 (C) 　　　 (D)

(11)已知函数若互不相等，且则的取值范围是

(A) 　　　　 (B) 　　　　　　 (C) 　　　　　　　 (D)

(12)已知双曲线的中心为原点，是的焦点，过F的直线与相交于A，B两点，且AB的中点为,则的方程式为

(A) 　 　　(B)

(C) 　　　　 (D)

第Ⅱ卷

本卷包括必考题和选考题两部分，第(13)题~第(21)题为必考题，每个试题考生都必须做答，第(22)题~第(24)题为选考题，考试根据要求做答。