
1.(2001年高考理综题)将4 mol A气体和2 mol B气体在2 L的容器中混合并在一定条件下发生如下反应:
2A(g)+B(g)  2C(g)
2C(g)
若经2 s(秒)后测得C的浓度为0.6 mol·L-1,现有下列几种说法:
①用物质A表示的反应的平均速率为0.3 mol·L-1·s-1
②用物质B表示的的反应的平均速率为0.6 mol·L-1·s-1
③2 s时物质A的转化率为70% ④2 s时物质B的浓度为0.7 mol·L-1,其中正确的是
A.①③ B.①④
C.②③ D.③④
|
教学 环节 |
教学内容 |
师生互动 |
|
复习 引入 |
1、 正比例函数、一次函数的几析式? 2、 正比例函数、一次函数的几析式中各有几个需要  确定的系数? 确定的系数? |
教师通过多媒体展示问题,学生思考后回答. |
 概念 形成 |
定义:在求一个函数时,如果已知这个函数的一般式,可以先把所求函数设为一般式,其中系数待定,然后根据题设条件求出这些待定系数的方法叫待定系数法. 例:二次函数的运用 已知二次函数f(x),f(0)=-5,f(-1)=-4,f(2)=5,求这个函数. 运用待定系数法解题步骤: 第一步:设出适当含有待定系数的解析式; 第二步:根据已知条件,列出含有待定系数的方程组; 第三步:解方程组,或消去待定系数,进而解决问题. 二次  函数在待定系数法中的设法: 函数在待定系数法中的设法:设法1:已知顶点坐标(m,n),可设y=a  ,再利用一 ,再利用一 个独立条件,求a. 个独立条件,求a.设法2:已知对称轴x=m,设  利用两个独立条件求a,b. 利用两个独立条件求a,b.设法3:已知最大或最小值n,可设 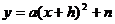 ,利用两个独立条件,求a,h. ,利用两个独立条件,求a,h.设法4:二次函数图像与x轴有两个交点时,设 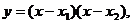 再 再 利用一个独立条件求a. 利用一个独立条件求a.练习:求下列二次函数的解析式 ①经过三点(3,0),(0,-3),(-2,5)  ②顶点(4,2),(2,0)在图像上  ③ ③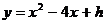 的顶点在 的顶点在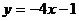 上 上 |
学生分组讨论并总结. 每种结论给出相应练  习. 习. 学生到黑板板演. |
|
概念 深化 |
给定哪些条件,才能求出一个具体的二次函数. |
学生分小组讨论,进行探索与研究. |
|
应用 举例 |
一根弹簧原长是12厘米,它能挂的重量不超过15kg,并且每挂重量1kg就伸长0.5厘米,挂后的弹簧长度y(cm)与挂重(kg)是一次函数的关系. (1) 求y与x的函数解析式; (2) 求自变量x的取值范围; (3) 画出这个函数的图像. |
例题由学生扮演完成,对出现的问题及时给予纠 正。学生 正。学生 练习,完成过后找学生口答。 练习,完成过后找学生口答。 |
|
归纳 小结 |
方法:求函数解析式的重要方法--待定系数法. 知识:用待定系数法求函数解析式. |
|

采用实例归纳, 自主探究,合作交流等方法;教学中通过列举例子,引导学生进行讨论和交流,
自主探究,合作交流等方法;教学中通过列举例子,引导学生进行讨论和交流,
并通过创设情境,让学生自主探索。
重点:用待定系数法求函数解析式;
难点:设出适当的解析式并用待定系数法求解析式。
3、情感目标 : (1)通过新旧知识的认识冲
: (1)通过新旧知识的认识冲 突,激发学生的求知欲;
突,激发学生的求知欲;
(2)通过合作学习,培养学生团结协作的品质。
2、 能力目标: (1)尝试设计有关一次、二次函数解析式问题,运用待定系数法求解;
(2)培养学生由特殊事例发现一般规律的归纳能力。
1、 知识目标:使学生掌握用待定系数法求解析式的方法;
15、已知二次函数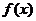 ,
,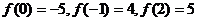 ,求这个函数的解析式.
,求这个函数的解析式.
14、一次函数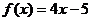 ,则
,则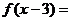 _________________
_________________ _
_ __________.
__________.
13、已知反比例函数过点(2,3), 则函数表达式为__________
则函数表达式为__________ _____________.
_____________.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com