
4.(08湖北卷理)设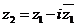 (其中
(其中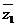 表示z1的共轭复数),已知z2的实部是
表示z1的共轭复数),已知z2的实部是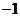 ,则z2的虚部为
.
,则z2的虚部为
.
3.复数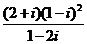 的值是 .
的值是 .
2.设复数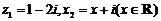 ,若
,若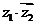 为实数,则x= .
为实数,则x= .
1. 复数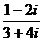 在复平面上对应的点位于第 象限.
在复平面上对应的点位于第 象限.
12. 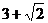
三 范例剖析
例1 (2008福建理) 若复数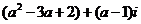 是纯虚数,则实数a的值为
是纯虚数,则实数a的值为
辨析:已知z, 互为共轭复数,若
互为共轭复数,若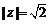 ,且
,且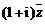 为实数,则
为实数,则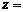 .
.
例2 复数z=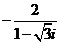 ,求1+z+z2的值;
,求1+z+z2的值;
辨析:(08四川延考理2)已知复数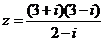 ,则
,则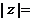
例3 设复数z满足|z+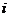 |+|z-
|+|z-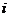 | = 2,求|z+
| = 2,求|z+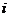 +1|的最小值.
+1|的最小值.
辨析:已知z0=2+2i,|z-z0|=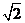 ,
,
(1)求复数z在复平面内对应的点的轨迹
(2)求z为何值时,|z|有最小值,并求出|z|有最小值,
四 巩固训练
11. 以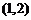 为圆心,2为半径的圆面(包括边界)
为圆心,2为半径的圆面(包括边界)
10.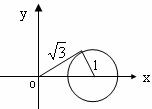 答案: ∵
答案: ∵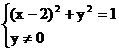 , 设k =
, 设k =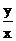 ,则k为过圆(x-2)2 + y2 = 1上点及原点
,则k为过圆(x-2)2 + y2 = 1上点及原点
|
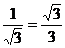 , 又∵y≠0 ,∴k≠0.由对称性,
, 又∵y≠0 ,∴k≠0.由对称性,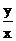 的取值范围是
的取值范围是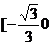 ∪(
∪(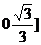 .
.
评析:本题考查复数的概念,以及转化与化归的数学思维能力,利用复数与解析几何、平面几何之间的关系求解.虚数一词又强调y≠0,这一易错点.
9. 答案: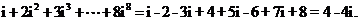
评析:考查复数的基本概念和运算
8.答案:由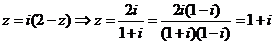 .
.
7. 答案: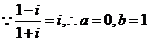 ,因此
,因此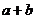 =1。
=1。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com