
18.(本题共2小题,其中第1小题6分,第2小题6分,满分12分)
定义在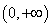 上的函数
上的函数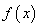 满足:对任意
满足:对任意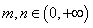 ,
,
都有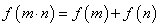 成立,且当
成立,且当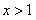 时,
时,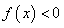 。
。
(1)求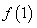 的值,并判断此函数在
的值,并判断此函数在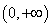 上的单调性;
上的单调性;
(2)当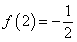 时,解不等式
时,解不等式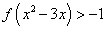 。
。
17.(本题满分12分)
已知函数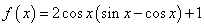 ,求此函数在区间
,求此函数在区间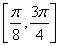 上的最大值和最小值,并求取得最值时
上的最大值和最小值,并求取得最值时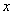 的值。
的值。
16.函数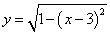 的图像上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是
( )
的图像上存在不同的三点到原点的距离构成等比数列,则以下不可能成为公比的数是
( )
A.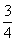 B.
B.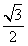 C.
C.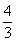 D.
D.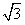
15.已知两点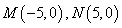 ,若直线上存在点
,若直线上存在点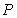 ,使
,使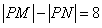 ,则称该直线为“
,则称该直线为“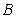 型直线”。现给出下列直线:
型直线”。现给出下列直线:
①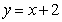 ; ②
; ②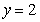 ; ③
; ③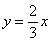 ; ④
; ④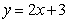 。
。
其中是“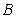 型直线”的是
( )
型直线”的是
( )
A.①② B.①③ C.②③ D.①④
14.已知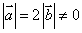 ,若关于
,若关于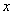 的方程
的方程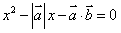 有实数根,则
有实数根,则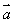 与
与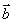 的夹角的取值范围为
( )
的夹角的取值范围为
( )
A.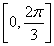 B.
B.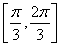 C.
C.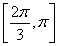 D.
D.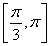
13.复数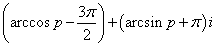 (
(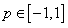 ,
,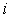 为虚数单位)在复平面内对应的点位于 ( )
为虚数单位)在复平面内对应的点位于 ( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
12.设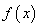 是定义在
是定义在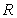 上的奇函数,且对于任意的
上的奇函数,且对于任意的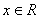 ,
,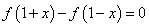 恒成立,当
恒成立,当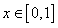 时,
时,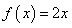 。若方程
。若方程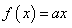 恰好有5个不同的解,则实数
恰好有5个不同的解,则实数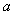 的取值范围是_______________。
的取值范围是_______________。
11.定义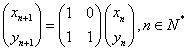 为向量
为向量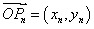 到向量
到向量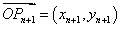 的一个矩阵变换,其中
的一个矩阵变换,其中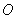 是坐标原点。已知
是坐标原点。已知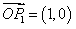 ,则
,则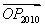 的坐标为_________。
的坐标为_________。
10.若对任意实数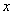 、
、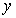 都有
都有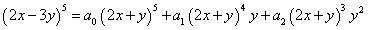
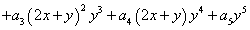 ,则
,则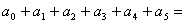 _______。
_______。
9.数列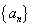 中,
中,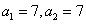 ,当
,当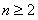 时,
时,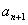 是积
是积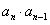 的个位数,则
的个位数,则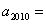 ______。
______。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com