7．有人曾用三首诗词来形容三大江的文化特色，如黄河文化是“黄河之水天上来，奔流到海不复还”；长江文化是“大江东去，浪淘尽，千古风流人物”；珠江文化是“海上生明月，天涯共此时”，“共此时”三字就很能体现广东文化的包容性与共时性。上述材料表明

　　 A．每个民族部以自已的文化

　　 B．我国各地区文化带有明显的区域特征

　　 C．文化有地域之别，无先进与落后之分

　　 D．人人都有自已的文化生活

6．张明在《地球村》专题小报中插入了一些用白描手法描绘的示意图，为提高小报的版面利用率，图片的环绕方式应该选择

　 A．浮于文字上方　 　　　　 B．衬于文字下方　 　　 C．四周型　　 　　　　　 D．上下型

5．历届奥运主题歌曲，均以鲜明的艺术风格给世人留下了难以忘怀的印象，使得奥林匹克精神更容易被大众所接受。汉城奥运会的主题歌曲是

　 A．马上芭蕾　　 　　　　　　 B．生命之杯　　 　　　　 C．手拉手　　 　　　　　 D．运动员进行曲

4. “一花独放不是春，百花齐放春满园。”这启示我们，在与世界文化交流中，处理好我和你的关系就必须

　　 A．尊重文化多样性　　 　　　　　　　　　　　　　　　　 B．重视文化继承性

　　 C．理解文化发展性　　 　　　　　　　　　　　　　　　　 D．懂得文化先进性

3．丹友首都哥本哈根滨海公园的雕塑作品《美人鱼》(见右图)，以其独特的艺术语言向人们展示了和平友谊的愿望。设计这类环境雕塑作品时，作者一般会从以下哪些因素着眼进行创作

　　 ①作品的呈现方式是否圆雕形式

　　 ②作品的主题内容是否与环境适合

　　 ③作品的体量大小是否与环境协调

　　 ④作品的主体形象是否是人物造型

　　 ⑤作品的艺术风格是否与环境统一

　　 A．①②③　　 　　　　　　 B．②③④

　　 C．①④⑤　　 　　　　　 D．②③⑤

2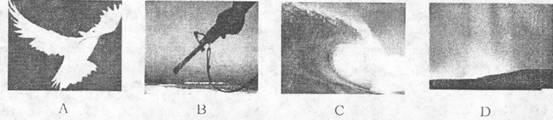．下列图片最能体现人类社会向往和平、友谊的是

1．北京奥运会主题曲《我和你》，所用的演唱形式是

　　　 A. 以独唱经主,加入了对唱　　 　　　　　　　　　　　 B. 以对唱以主,加入了合唱

　　　 C. 不独唱以主,加入了合唱　　 　　　　　　　　　　　 D. 以对唱以主,加入了重唱

1形如的递归式，其通项求法为

=

例1已知，，(n≥2),求

解：=+=

2形如型的递归式，其通项求法为

例2设数列中，，且，求.

解：当n≥2时，，依题意，有，两式相减得：，故，∴，

∴，由于满足上式∴

3形如型的一阶递推式，可化为的形式，求解

例3设数列中，，且，(n≥2),求.

解：，=

4形如型的递推式，两边同除以，得

转化为第一种形式求解.

例4．设数列中，，且，(n≥2),求.

解：两边同除以得，，令，则，

∴==

∴,本题也可以将原式两边同除以得，，令，则，则原式变为再按一阶递推数列的求法也可求出.

5特征方程:对于二阶线性递推数列，满足，　　　　　　 ①

其中a,b是常数，且.若有等比数列满足公式①，则x必满足相应的方程

　　 ②； 反之，特征方程②有一个实根α，则等比数列必满足递推公式①；当，方程②有两个不相等的实根α，β，则数列，均是①的解，并且对任意常数，有也是①的解.如果给出初始条件，则可以求出通项公式.

例5已知数列中，，，且，求.

解：解法1，(特征根法)对于相应的特征根方程有两个不等的实根2，3，则它的通解为，把，代入得，，，，故所求的通解是：

解法2：(待定系数法)设，即，则数列的递推公式可以改写成，即：

==…=①==…=②由①、②得

6韦达定理法：例如已知，求通项，通过去根号，整理得：，以代替上式中的n得：，这样与是二次方程的两根，由韦达定理知，再仿照5特征根法求解.

7简单的分式数列：设，满足递推关系，其中n≥2，且初始值.若方程有两个不等的实根p,q,则

，这里，即是以的等比数列；若

方程有唯一的实根p,则，这里，即是以k为公差的等差数列.

例7已知数列中，，，求的通项公式.

解：解方程得，有两个不等的实根1和-2，

，

8可转化为等差(比)的数列：

例8若数列中，，，且 n≥1，求通项公式.

解：显然数列各项均为不小于1的正值，开方得，配方有

，因为，所以，故是等差数列，得，. 例9已知中，，，求的通项公式.

解：由条件得，所以数列是等差数列，，.例10已知，且，求的通项公式.

解：解方程得，有两解，由此可得，，两式相除有：，两边取对数得，所以数列是等比数列，所以，，本题也可以反复迭代得

=…==由此解出：

21. (本小题满分14分)

　已知数列的前n项和为s,且a=1,数列是公差为2的等差数列。(1)求a,a的值；(2)证明：数列是等比数列；(3)求数列的前n项和T

09-10学年上学期期中考试

20. (本小题满分12分)

设向量=(sinx,cosx),=(cosx,cosx),xR.函数 f(x)= . (+)

(1)求函数f(x)的最大值与最小正周期；

(2)求使不等式f(x) 成立的x的取值范围。