
1、圆台的一个底面周长是另一个底面周长的 倍,母线长为
倍,母线长为 ,圆台的侧面积为
,圆台的侧面积为 ,则圆台较小底面的半径为( )
,则圆台较小底面的半径为( )
(A) (B)
(B) (C)
(C) (D)
(D)

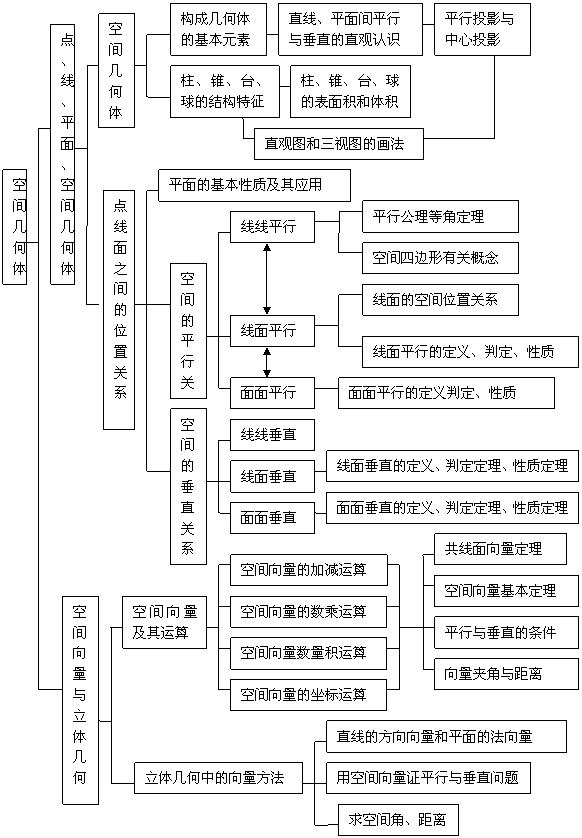
4.空间几何中的向量方法
例13. 如下图,直棱柱ABC-A1B1C1的底面△ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
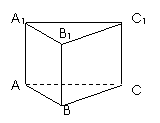 (1)求BN的长;
(1)求BN的长;
(2)求异面直线BA与1CB1的余弦值;
(3)求证:A1B⊥C1M.
[解法]:∵AC⊥BC,CC1⊥面ABC,
∴可以建立如图所示的坐标系

(1)依题意得B(0, 1,0),N(1,0,1),
∴| |=
|= =
= .
.
(2)A1(1,0,2),B(0,1,0),C(0,0,0),B1(0,1,2),
∴ =(1,-1,2),
=(1,-1,2), =(0,1,2),
=(0,1,2), ·
· =3,|
=3,| |=
|= ,|
,| |=
|= .
.
∴cos〈 ,
, 〉=
〉= =
= .
.
所以,异面直线BA与1CB1的余弦值为
(3)证明:C1(0,0,2),M( ,
, ,2),
,2),
 =(-1,1,-2),
=(-1,1,-2), =(
=( ,
, ,0),∴
,0),∴ ·
· =0,∴A1B⊥C1M.
=0,∴A1B⊥C1M.
[点评]底面有直角的直棱柱适合建立坐标系的条件,可以用两点间的距离公式,数量积的夹角公式,用坐标法求点点距、向量夹角特别注意异面直线角的范围(0, ],而向量角的范围为[0,π]
],而向量角的范围为[0,π]
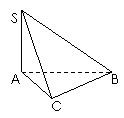 [变式与拓展]在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC=
[变式与拓展]在三棱锥S-ABC中,∠SAB=∠SAC=∠ACB=90°,AC=2,BC= ,SB=
,SB= .
.
(1)求证:SC⊥BC;
(2)求SC与AB所成角的余弦值.
[解法一]:如下图,取A为原点,AB、AS分别为y、z轴建立空间直角坐标系,则有AC=2,BC= ,SB=
,SB= ,得B(0,
,得B(0, ,0)、S(0,0,2
,0)、S(0,0,2 )、C(2
)、C(2 ,
, ,0),
,0), =(2
=(2 ,
, ,-2
,-2 ),
), =(-2
=(-2 ,
, ,0).
,0).

(1)∵ ·
· =0,∴SC⊥BC.
=0,∴SC⊥BC.
(2)设SC与AB所成的角为α,∵ =(0,
=(0, ,0),
,0), ·
· =4,|
=4,| ||
||  |=4
|=4 ,∴cosα=
,∴cosα= ,即为所求.
,即为所求.
[解法二]:(1)∵SA⊥面ABC,AC⊥BC,AC是斜线SC在平面ABC内的射影,∴SC⊥BC.
(2)如下图,过点C作CD∥AB,过点A作AD∥BC交CD于点D,连结SD、SC,则∠SCD为异面直线SC与AB所成的角.∵四边形ABCD是平行四边形,CD= ,SA=2
,SA=2 ,SD=
,SD= =
= =5,∴在△SDC中,由余弦定理得cos∠SCD=
=5,∴在△SDC中,由余弦定理得cos∠SCD= ,即为所求.
,即为所求.
例14.如图,在四棱锥 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱 底面ABCD,
底面ABCD,
 ,E是PC的中点,作
,E是PC的中点,作 交PB于点F.
交PB于点F.
 (1)证明
(1)证明  平面
平面 ;
;
(2)证明 平面EFD;
平面EFD;
(3)求二面角 的大小.
的大小.
 [解法]:如图所示建立空间直角坐标系,D为坐标原点.设
[解法]:如图所示建立空间直角坐标系,D为坐标原点.设
⑴证明:连结AC,AC交BD于G.连结EG.
依题意得
 底面ABCD是正方形,
底面ABCD是正方形,  是此正方形的中心,
是此正方形的中心,
故点G的坐标为 且
且
 . 这表明
. 这表明 .
.
而 平面EDB且
平面EDB且 平面EDB,
平面EDB, 平面EDB。
平面EDB。
⑵证明:依题意得 。又
。又
故
 , 由已知
, 由已知 ,且
,且 所以
所以 平面EFD.
平面EFD.
(3)解:设点F的坐标为 则
则
从而 所以
所以
由条件 知,
知, 即
即 解得
解得 
 点F的坐标为
点F的坐标为 且
且
 ,即
,即 ,
,
故 是二面角
是二面角 的平面角.
的平面角.
∵ 且
且


 ,
,
所以,二面角C-PC-D的大小为
[点评]考查空间向量数量积及其坐标表示,运用向量数量积判断向量的共线与垂直,用向量证明线线、线面、面面的垂直与平行关系。
[变式与拓展]如图,已知矩形ABCD所在平面外一点P,PA⊥平面ABCD,
E、F分别是AB、
 PC的中点.
PC的中点.
(1)求证:EF∥平面PAD;
(2)求证:EF⊥CD;
(3)若ÐPDA=45°,求EF与平面ABCD所成的角.
证明:如图,建立空间直角坐标系A-xyz,
设AB=2a,BC=2b,PA=2c,则:A(0, 0, 0),
B(2a, 0, 0),C(2a, 2b, 0),D(0, 2b, 0),
P(0, 0, 2c)∵ E为AB的中点,F为PC的中点
∴ E (a, 0, 0),F (a, b, c)
 (1)∵
(1)∵ =(0, b, c),
=(0, b, c), =(0, 0, 2c),
=(0, 0, 2c), =(0, 2b, 0)
=(0, 2b, 0)
∴ =(+) ∴
=(+) ∴ 与
与 、
、 共面
共面
又∵ E Ï 平面PAD ∴ EF∥平面PAD.
(2)∵ =(-2a, 0, 0 )
∴·=(-2a, 0, 0)·(0, b, c)=0 ∴ CD⊥EF.
(3)若ÐPDA=45°,则有2b=2c,即 b=c,∴ =(0, b, b),
=(0, 0, 2b) ∴ cos á,ñ==
∴ á,ñ= 45°
∵ ⊥平面AC,∴ 是平面AC的法向量
∴ EF与平面AC所成的角为:90°-á,ñ= 45°.
 例15.如图,在正四棱柱
例15.如图,在正四棱柱 中,已知
中,已知 ,
,
 、
、 分别为
分别为 、
、 上的点,且
上的点,且
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求点 到平面
到平面 的距离.
的距离.
解:(Ⅰ)以 为原点,以
为原点,以 、
、 、
、 的正向分别为
的正向分别为 轴、
轴、 轴、
轴、
 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则

于是
 且
且

 平面
平面
(Ⅱ)由(Ⅰ)知, 为平面
为平面 的一个法向量,
的一个法向量,
 向量
向量 在
在 上的射影长即为
上的射影长即为 到平面
到平面 的距离,设为
的距离,设为 ,于是
,于是

故点 到平面
到平面 的距离为
的距离为
例16.如图,在四棱锥P-ABCD中,底面ABCD为矩形,侧棱PA⊥底面ABCD,AB=,BC=1,PA=2,E为PD的中点.
(Ⅰ)求直线AC与PB所成角的余弦值;
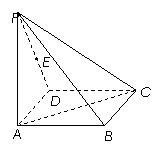 (Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
(Ⅱ)在侧面PAB内找一点N,使NE⊥面PAC,
并求出N点到AB和AP的距离.
解:方法一、(1)设AC∩BD=O,连OE,则OE//PB,
∴∠EOA即为AC与PB所成的角或其补角.
在△AOE中,AO=1,OE=

∴
即AC与PB所成角的余弦值为 .
.
(2)在面ABCD内过D作AC的垂线交AB于F,则 .
.
连PF,则在Rt△ADF中
设N为PF的中点,连NE,则NE//DF,
∵DF⊥AC,DF⊥PA,∴DF⊥面PAC,从而NE⊥面PAC.
∴N点到AB的距离 ,N点到AP的距离
,N点到AP的距离
方法二、(Ⅰ)建立如图所示的空间直角坐标系,
则A、B、C、D、P、E的坐标为A(0,0,0)、
 B(
B( ,0,0)、C(
,0,0)、C( ,1,0)、D(0,1,0)、
,1,0)、D(0,1,0)、
P(0,0,2)、E(0, ,1),
,1),
从而
设 的夹角为θ,则
的夹角为θ,则

∴AC与PB所成角的余弦值为 .
.
(Ⅱ)由于N点在侧面PAB内,故可设N点坐标为(x,O,z),则 ,由NE⊥面PAC可得,
,由NE⊥面PAC可得,
 ∴
∴
即N点的坐标为 ,从而N点到AB、AP的距离分别为1,
,从而N点到AB、AP的距离分别为1, .
.
3.距离与角
 例11.已知
例11.已知 所在的平面互相垂直,且AB=BC=BD,
所在的平面互相垂直,且AB=BC=BD, ,求:
,求:
⑴.直线AD与平面BCD所成角的大小;
⑵.直线AD与直线BC所成角的大小;
⑶.二面角A-BD-C的余弦值.
⑴如图,在平面ABC内,过A作AH⊥BC,垂足为H,
则AH⊥平面DBC,∴∠ADH即为直线AD与平面BCD所成的角
由题设知△AHB≌△AHD,则DH⊥BH,AH=DH,∴∠ADH=45°
⑵∵BC⊥DH,且DH为AD在平面BCD上的射影,
∴BC⊥AD,故AD与BC所成的角为90°
⑶过H作HR⊥BD,垂足为R,连结AR,则由三垂线定理知,AR⊥BD,故∠ARH为二面角A-BD-C的平面角的补角 设BC=a,则由题设知,AH=DH= ,在△HDB中,HR=
,在△HDB中,HR= a,∴tanARH=
a,∴tanARH= =2
=2
故二面角A-BD-C的余弦值的大小为
[点评]:本题着眼于让学生掌握通性通法几何法在书写上体现:“作出来、证出来、指出来、算出来、答出来”五步斜线和平面所成的角是一个直角三角形所成的锐角,它的三条边分别是平面的垂线段、斜线段及斜线段在平面内的射影。因此求直线和平面所成的角,几何法一般先定斜足、再作垂线找射影、通过解直角三角形求解;向量法则利用斜线和射影的夹角或考虑法向量,设
 为直线
为直线 与平面
与平面 所成的角,
所成的角, 为直线
为直线 的方向向量
的方向向量 与平面
与平面 的法向量
的法向量 之间的夹角,则有
之间的夹角,则有 或
或 (如图)
(如图)

特别地  时,
时, ,
, ;
; 时,
时,  ,
, 或
或 。
。
⑴用两面垂直的性质作垂线,找垂足的位置作出线面角,⑵利用三垂线定理证,⑶利用对称性定义法作二面角
 [变式与拓展]如图,BCD是等腰直角三角形,斜边CD的长等于点P到BC的距离,D是P在平面BCD上的射影.
[变式与拓展]如图,BCD是等腰直角三角形,斜边CD的长等于点P到BC的距离,D是P在平面BCD上的射影.
⑴.求PB与平面BCD所成角;
⑵.求BP与平面PCD所成的角.
[解法]
⑴. PD⊥平面BCD,∴BD是PB在平面BCD内的射影,
∴∠PBD为PB与平面BCD所成角,BD⊥BC,
由三垂线定理得BC⊥BD,∴BP=CD,设BC=a,
则BD=a,BP=CD= a∴在Rt△BPD中,
a∴在Rt△BPD中,
cos∠DBP= ∴∠DBP=45°, 即PB与平面BCD所成角为45°.
∴∠DBP=45°, 即PB与平面BCD所成角为45°.
⑵.过B作BE⊥CD于E,连结PE,PD⊥平面BCD得PD⊥BE,∴BE⊥平面PCD,
∴∠BPE为BP与平面PCD所成的角,在Rt△BEP中,BE= a, BP=
a, BP= a,∴∠BPE=30° 即BP与平面PCD所成角为30°
a,∴∠BPE=30° 即BP与平面PCD所成角为30°
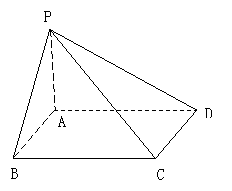 例12.在四棱锥P-ABCD中,已知ABCD为矩形,PA ⊥平面ABCD,设PA=AB=a,BC=2a,求二面角B-PC-D的大小
例12.在四棱锥P-ABCD中,已知ABCD为矩形,PA ⊥平面ABCD,设PA=AB=a,BC=2a,求二面角B-PC-D的大小
 解析1.定义法 过D作DE ⊥PC于E,过E作EF ⊥PC于F,连接FD,由二面角的平面角的定义可知
解析1.定义法 过D作DE ⊥PC于E,过E作EF ⊥PC于F,连接FD,由二面角的平面角的定义可知 是所求二面角B-PC-D的平面角。求解二面角B-PC-D的大小只需解△DEF即可
是所求二面角B-PC-D的平面角。求解二面角B-PC-D的大小只需解△DEF即可
[解法一]过D作DE ⊥PC于E,过E作EF ⊥PC于F,连接FD,由二面角的平面角的定义可知 是所求二面角B-PC-D的平面角
是所求二面角B-PC-D的平面角
在四棱锥P-ABCD中, PA ⊥平面ABCD且ABCD为矩形,∵AD⊥DC∴PD⊥DC
∵PA=a,AD=BC=2a,∴PD= ,PC=
,PC= ,DE=
,DE= ,CE=
,CE=
同理在Rt△PBC中, ,
,
在Rt△EFC中,FC= , 在Rt△DFC中,DF=
, 在Rt△DFC中,DF= ,
,
在△DEF中由余弦定理cos =
=
所求二面角B-PC-D的余弦值为
解析2.垂面法 易证面PAB⊥面PBC,过A作AM ⊥BP于M,显然AM ⊥面PBC,从而有AM ⊥PC,同法可得AN ⊥PC,再由AM与AN相交与A得PC ⊥面AMN。设面AMN交PC于Q,则 为二面角B-PC-D的平面角;再利用三面角公式可解。
为二面角B-PC-D的平面角;再利用三面角公式可解。
[解法二]
 略
略
解析3.利用三垂线求解 把四棱锥P-ABCD补成如图的直三棱柱PAB-EDC,显然二面角E-PC-D与二面角D-PC-B互补,转化为求二面角E-PC-D。
易证面PEDA ⊥PDC,过E作EF ⊥ PD于F,显然PF ⊥面PDC,在面PCE内,过E作EG ⊥PC于G,连接GF,由三垂线得GF⊥ PC 即 为二面角E-PC-D的平面角,只需解△EFG即可
为二面角E-PC-D的平面角,只需解△EFG即可
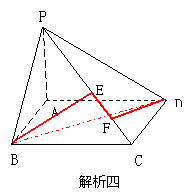
解析4.在面PDC内,分别过D、B作DE ⊥PC
于E,
BF ⊥PC于F,连接EF即可。
利用平面知识求BF、EF、DE的长度,
再利用空间余弦定理求出q 即可
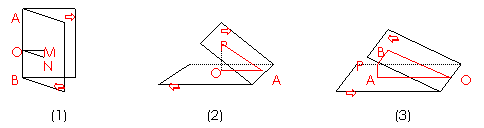
[点评].用几何法求二面角的方法比较多,常见的有:
(1)定义法, 在棱上的点分别作棱的垂线,如解析1
(2)三垂线求解 ,在棱上的点分别作棱的垂线,如解析2
(3)垂面法, 在棱上的点分别作棱的垂线,如解析3
用几何法将二面角转化为其平面角,要掌握以下三种基本做法:①直接利用定义,图(1).②利用三垂线定理及其逆定理,图 (2).最常用。③作棱的垂面,图(3).
2.平行与垂直
例8.已知:正方体 ,
, ,E为棱
,E为棱 的中点.
的中点.
⑴求证: ;
;
⑵求证: 平面
平面 ;⑶求三棱锥
;⑶求三棱锥 的体积
的体积


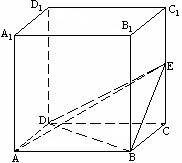 证明:连结
证明:连结 ,则
,则 //
// , ∵
, ∵ 是正方形,∴
是正方形,∴ .
.
∵ 面
面 ,∴
,∴ .
.
又 ,∴
,∴ 面
面 .
. 
∵ 面
面 ,∴
,∴ ,
,
∴ .
.

⑵证明:作 的中点F,连结
的中点F,连结 .
.
∵ 是
是 的中点,∴
的中点,∴

 ,
,
∴四边形 是平行四边形,∴
是平行四边形,∴  .
. 
∵ 是
是 的中点,∴
的中点,∴ ,
,
又 ,∴
,∴ .
.
∴四边形 是平行四边形,
是平行四边形, //
// ,
,
∵ ,
, ,
,
∴平面 面
面 .
.
又 平面
平面 ,∴
,∴ 面
面

例 9. 多面体
9. 多面体 中,
中, ,
, ,
, ,
, 。
。
(1)求证: ;
;
(2)求证: 。
。
证明:(1)∵



∴

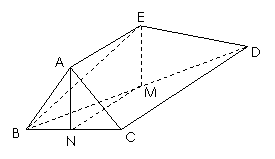 (2)令
(2)令 中点为
中点为 ,
, 中点为
中点为 ,连结
,连结 、
、

∵ 是
是 的中位线
的中位线
∴

又∵

∴
∴
∴
∵ 为正
为正
∴
∴
又∵ ,
,
∴四边形 为平行四边形
为平行四边形
∴
∴
例10.如图四边形 是菱形,
是菱形, 平面
平面 ,
,  为
为 的中点. 求证:
的中点. 求证:
 ⑴
⑴  ∥平面
∥平面 ;
;
⑵ 平面 平面
平面 .
.
解:证:设
 ,连
,连 。
。
⑴ ∵ 为菱形, ∴
为菱形, ∴  为
为 中点,又
中点,又 为
为 中点。
中点。
∴ ∥
∥
又 ,
,  ∴
∴ ∥
∥
⑵ ∵ 为菱形, ∴
为菱形, ∴ ,
,
又∵ ,
,  ∴
∴
又  ∴
∴ 又
又
∴
5.使学生更好地理解多面体与旋转体的体积及其计算方法,能够熟练地使用分割与补形求体积,提高空间想象能力、推理能力和计算能力.
[考纲要求]
(1)掌握平面的基本性质,会用斜二测的画法画水平放置的平面图形的直观图,能够画出空间两条直线、直线和平面的各种位置关系的图形,能够根据图形想象它们的位置关系
(2)了解空两条直线的位置关系,掌握两条直线平行与垂直的判定定理和性质定理,掌握两条直线所成的角和距离的概念(对于异面直线的距离,只要求会计算已给出公垂线时的距离)
(3)了解空间直线和平面的位置关系,掌握直线和平面平行的判定定理和性质定理,理解直线和平面垂直的判定定理和性质定理,掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念,了解三垂线定理及其逆定理
(4)了解平面与平面的位置关系,掌握两个平面平行的判定定理和性质定理。掌握二面角、二面角的平面角、两个平面间的距离的概念,掌握两个平面垂直的判定定理和性质定理。
(5)会用反证法证明简单的问题
(6)了解多面体的概念,了解凸多面体的概念
(7)了解棱柱的概念,掌握棱柱的性质,会画直棱柱的直观图。
(8)了解棱锥的概念,掌握正棱锥的性质,会画正棱锥的直观图
(9)了解正多面体的概念,了解多面体的欧拉公式。
(10)了解球的概念,掌握球的性质,掌握球的表面积、体积公式.




[知识纵横]



















[教法指引]
⑴须明确《直线、平面、简单几何体》中所述的两个平面是指两个不重合的平面
⑵与“直线与直线平行”、“直线与平面平行”的概念一样“平面与平面平行”是
指“二平面没有公共点” .由此可知,空间两个几何元素(点、直线、平面称为空间三个几何元素)间“没有公共点”时,它们间的关系均称为“互相平行”要善于运用平面与平面平行的定义所给定的两平面平行的最基本的判定方法和性质.
⑶注意两个平行平面的画法--直观地反映两平面没有公共点,将表示两个平面的平行四边形画成对应边平行。两个平面平行的写法与线、线平行,线、面平行的写法一议,即将“平面 平行于平面
平行于平面 ”,记为“
”,记为“ ∥
∥ ”
” 
⑷空间两个平面的位置关系有且只有“两平面平行”和“两平面相交”两种关系.
⑸在明确“两个平行平面的公垂线”、“两个平行平面的公垂线段”、“两个平行平面的距离”的概念后,应该注意到,两平行平面间的公垂线段有无数条,但其长度都相等--是唯一确定的值,且两平行平面间的公垂线段,是夹在两平行平面间的所有线段中最短的线段,此外还须注意到,两平行平面间的距离可能化为“其中一个平面内的直线到另一个平面的距离”又可转化为“其中一个面内的一个点到另一个平面的距离.
⑹三种空间角,即异面直线所成角、直线与平面所成角。平面与平面所成二面角。它们的求法一般化归为求两条相交直线的夹角,通常“线线角抓平移,线面角找射影,面面角作平面角”而达到化归目的,有时二面角大小出通过cos =
= 来求
来求
⑺有七种距离,即点与点、点到直线、两条平行直线、两条异面直线、点到平面、平行于平面的直线与该平面、两个平行平面之间的距离,其中点与点、点与直线、点到平面的距离是基础,求其它几种距离一般化归为求这三种距离,点到平面的距离有时用“体积法”来求。
[典例精析]
1, 空间几何体及三视图
例1.用一些棱长为1cm的小正方体码放成一个几何体,图1为其俯视图,图2为其主视图则这个几何体的体积最大是 7
cm3. 




图1(俯视图)
图2(主视图)
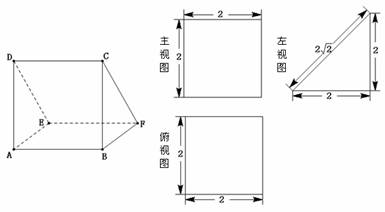
例2.一个多面体的直观图及三视图如图所示,则多面体 的体积为 ▲ .
的体积为 ▲ .







例4.右图是由一些相同的小正方体构成的几何体的三视图,这些相同的小正方体共有▲ 个.5
例5.如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是
 。
。





例 6.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为
6.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B-AC-D,则四面体ABCD的外接球的体积为


例7.一个几何体的三视图中,正视图和侧视图都是矩形,俯视图是等腰直角三角形(如图),根据图中标注的长度,可以计算出该几何体的表面积是 12+4 .
.
4.在学生解答问题的过程中,注意培养他们的语言表述能力和“说话要有根据”的逻辑思维的习惯、提高思维品质.使学生掌握化归思想,特别是将立体几何问题转化为平面几何问题的思想意识和方法,并提高空间想象能力、推理能力和计算能力.
3.通过复习,使学生更好地掌握多面体与旋转体的有关概念、性质,并能够灵活运用到解题过程中.通过教学使学生掌握基本的立体几何解题方法和常用解题技巧,发掘不同问题之间的内在联系,提高解题能力.
2.在掌握空间角(两条异面直线所成的角,平面的斜线与平面所成的角及二面角)概念的基础上,掌握它们的求法(其基本方法是分别作出这些角,并将它们置于某个三角形内通过计算求出它们的大小);在解决有关空间角的问题的过程中,进一步巩固关于直线和平面的平行垂直的性质与判定的应用,掌握作平行线(面)和垂直线(面)的技能;通过有关空间角的问题的解决,进一步提高学生的空间想象能力、逻辑推理能力及运算能力.
1.在掌握直线与平面的位置关系(包括直线与直线、直线与平面、平面与平面间的位置关系)的基础上,研究有关平行和垂直的的判定依据(定义、公理和定理)、判定方法及有关性质的应用;在有关问题的解决过程中,进一步了解和掌握相关公理、定理的内容和功能,并探索立体几何中论证问题的规律;在有关问题的分析与解决的过程中提高逻辑思维能力、空间想象能力及化归和转化的数学思想的应用.
13. 一个几何体的三视图如右图所示,其中正视图和侧视
一个几何体的三视图如右图所示,其中正视图和侧视
图是腰长为6的两个全等的等腰直角三角形.
(Ⅰ)请画出该几何体的直观图,并求出它的体积;
(Ⅱ)用多少个这样的几何体可以拼成一个棱长为
6的正方体ABCD-A1B1C1D1? 如何组拼?试证明你的结论;
(Ⅲ)在(Ⅱ)的情形下,设正方体ABCD-A1B1C1D1
的棱CC1的中点为E, 求平面AB1E与平面ABC所成二面
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com