2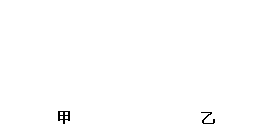．甲、乙两电路中，当a、b两端与e、f两端分别加上220V的交流电压时，测得c、d间与g、h间的电压均为110V。若分别在c、d两端与g、h两端加上110V的交流电压，则a、b间与e、f间的电压分别为(　B 　)

A．220V、220V

B．220V、110V

C．110V、110V　　　　　　　　　　　

D．220V、0

3、 如图所示的闭合电路中，当滑动变阻器的触点分别接b和a时,两只理想电压表V1和V2分别有两个读数U1和U1'、U2和U2'．设△U1=｜U1'- Ul｜,△U2=｜U2'-U2｜，电池内阻不为零，则(　 A； )． 

A. △U1>△U2　　 B．△U1=△U2

C．△U1<△U2　　 D．前三种情况均可能

18．解答：断开时，、间的电阻为，于是

　　　　　 　　　　　　　①

闭合时，设流过甲表的电流为I，则流过乙表的电流为2I，于是

　　　　　 　　　　　　　②

由此可解得　　　 　　　　　　　　　　　　　③

　　　　　　　　 　　　　　　　　　　　　　　　④

18．如图所示电路中，甲、乙两个毫安表的内阻均为6Ω，R₃＝R₄＝12Ω，S断开时，AB之间电阻为3Ω，S闭合时，甲、乙两个毫安表的示数之比为∶2，求R₁、R₂的阻值各为多少？

17．解析：(1)感应电动势E＝ B l v，感应电流　 I=E/R

　∴I ＝ 0时，v ＝ 0

　此时，＝1(m)

(2)初始时刻，金属直杆切割磁感线速度最大，产生的感应电动势和感应电流最大

当感应电流为最大值的一半时，

安培力＝ 0.02 N

向右运动时：F + f ＝ m a

F ＝ m a － f ＝ 0.18 N，方向与x轴正方向相反

向左运动时：F － f ＝ m a

F ＝ m a + f ＝ 0.22 N，方向与x轴正方向相反

(3)开始时 v ＝ v₀ ，

　　　 F + f ＝ m a　F ＝ m a － f ＝

　　∴当v₀ ＜ 　＝ 10 m/s 时，F ＞0，方向与x轴正方向相反

　　当v₀ ＞ 　＝ 10 m/s 时，F ＜0，方向与x轴正方向相同

17．如图所示，两条互相平行的光滑金属导轨位于水平面内，距离为l ＝0.2m，在导轨的一端接有阻值为R ＝ 0.5Ω的电阻，在X ≥ 0处有一与水平面垂直的均匀磁场，磁感强度B ＝ 0.5T。一质量为m ＝ 0.1kg的金属直杆垂直放置在导轨上，并以v₀＝2m/s的初速度进人磁场，在安培力和一垂直于杆的水平外力 F的共同作用下作匀变速直线运动，加速度大小为a ＝ 2m/s²，方向与初速度方向相反。设导轨和金属杆的电阻都可以忽略，且接触良好，求：

(1)电流为零时金属杆所处的位置；

(2)电流为最大值的一半时施加在金属杆上外力 F的大小和方向；

(3)保持其他条件不变，而初速度v₀取不同值，求开始时F的方向与初速度v₀取值的关系。

16．解析：(1)对金属块A用动能定理　　　　　　　　　　 ①

　　　　　 所以电场强度大小　　　　　　　　　　　　　　　　　　 ②

　　　　　 方向水平向右　　　　　　　　　　　　　　　　　　　　　　　 ③

　　　　　 (2)A、B碰撞，由系统动量守恒定律得

　　　　　 　　　　　　　　　　　　　　　　　　　　④

　　　　　 用代入解得　　　　　　　　　　　　　　　　　 ⑤

　　　　　 B碰后做匀速运动，碰到挡板的时间

　　　　　　　　　　　　　　　　　　　　　　　　 ⑥

A的加速度　　　　　　　　　　　　　　　　　　　　　　　 ⑦

A在段时间的位移为

　　　　　　　　　　　 ⑧

因，故A第二次与B相碰必在B与C相碰之后　　　　　　　　　 ⑨

(3)B与C相碰，由动量守恒定律可得　　　　　　　　 ⑩

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 　 　　⑾

A从第一次相碰到第二次与B相碰的位移为L，因此电场力做的功

_⑿

16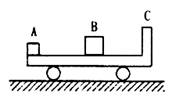．如图所示，长为2L的板面光滑且不导电的平板小车C放在光滑水平面上，车的右端有块挡板，车的质量，绝缘小物块B的质量。若B以一定速度沿平板向右与C车的挡板相碰，磁后小车的速度总等于碰前物块B速度的一半。今在静止的平板车的左端放一个带电量、质量为的小物块A，将物块B放在平板车的中央，在整个空间加上一个水平方向的匀强电场时，金属块A由静止开始向右运动，当A以速度与B发生碰撞，碰后A以的速率反弹回来，B向右运动，

(1)求匀强电场的场强大小和方向。

(2)若A第二次和B相碰，判断是在B与C相碰之前还是相碰之后？

(3)A从第一次与B相碰到第二次与B相碰这个过程中，电场力对A做了多少功？

15．解析： 粒子从a点出发，在电场中加速和在磁场中偏转，回到MN上的b点，轨迹如图所示

(1)粒子在电场中加速运动时，有

解得：　　　　 ①

由：　　　　　　 　　　　　　　　　　　

得：粒子在中间磁场通过的圆弧所对的圆心角为30°　　　　　 ②

粒子在中间磁场通过的圆弧半径为： 　

由几何关系得：

　　　　　　 　　　　　　　　　　　　　　　 ③

(2)粒子在右边磁场中运动：其圆弧对应的圆心角为　α＝120°

则：　　　　　　　　　　　　　 ④

粒子在电场中加速时：

　　　　　　　　　　⑤

根据对称性：

　　　　⑥

(3)由轨迹图得：

　　　　　　⑦

　　　　　　⑧

再由周期性可得：

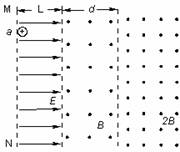
15．如图所示，水平方向的匀强电场的场强为E，场区宽度为L，竖直方向足够长。紧挨着电场的是垂直于纸面向外的两个匀强磁场区域，其磁感应强度分别为B和2B。一个质量为m，电量为q的带正电粒子，其重力不计，从电场的边界MN上的a点由静止释放，经电场加速后进入磁场，经过时间穿过中间磁场，进入右边磁场后能按某一路径再返回到电场的边界MN上的某一点b，途中虚线为场区的分界面。求：

(1)中间场区的宽度d；

(2)粒子从a点到b点所经历的时间；

(3)当粒子第次返回电场的MN边界时与出发点之间的距离。

14.解析： (1)电子在加速电场中运动，根据动能定理，有

∴　　　　　　　　　①　

(2)因为每个电子在板A、B间运动时，电场均匀、恒定，故电子在板A、B间做类平抛运动，在两板之外做匀速直线运动打在屏上。在板A、B间沿水平方向运动时，有

竖直方向，有　　

所以　　　　　　　　　　②　

只要偏转电压最大时的电子能飞出极板打在屏上，则所有电子都能打屏上。所以

，　　　　　　　③　

(3)要保持一个完整波形，荧光屏必须需每隔周期T，回到初始位置。

设某个电子运动轨迹如图所示，有

　　④

又知，

联立得　　　　　⑤

由相似三角形的性质，得　　　　　　　⑥　

则　　　　　　　　　　⑦

峰值为　　　　　　　　　⑧

波形长度为　　　　　　　　　　　 ⑨

波形如下图所示。