
2.设q是第二象限角,则必有( )。
A、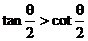 B、
B、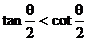
C、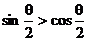 D、
D、
1.若 ,且cosa>sinb,那么下列关系式中正确的是( )。
,且cosa>sinb,那么下列关系式中正确的是( )。
A、 B、
B、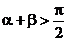 C、
C、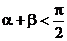 D、
D、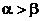
21.(本小题满分13分)
已知数列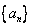 满足:
满足: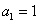 ,
,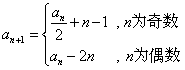 ,记
,记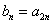 (n∈N*),
(n∈N*),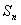 为数列
为数列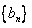 的前n项和.
的前n项和.
(Ⅰ)证明数列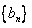 为等比数列,并求其通项公式;
为等比数列,并求其通项公式;
(Ⅱ)若对任意n∈N*且n≥2,不等式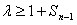 恒成立,求实数
恒成立,求实数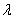 的取值范围;
的取值范围;
(Ⅲ)令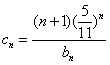 ,证明:
,证明: (n∈N*).
(n∈N*).
[解](Ⅰ)因为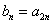 ,由已知可得,
,由已知可得,
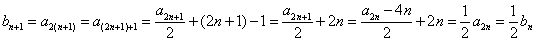 .(3分)
.(3分)
又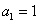 ,则
,则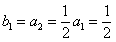 .
(4分)
.
(4分)
所以数列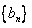 是首项和公比都为
是首项和公比都为 的等比数列,故
的等比数列,故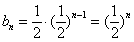 .
(5分)
.
(5分)
20.(本小题满分13分)
已知两圆 和
和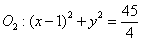 ,动圆P与
,动圆P与 ⊙O1外切,且与⊙O2内切.
⊙O1外切,且与⊙O2内切.
(Ⅰ)求动圆圆心P的轨迹方程;
(Ⅱ)过点M(5,0)作直线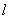 与点P的轨迹交于不同两点A、B,试推断是否存在直线
与点P的轨迹交于不同两点A、B,试推断是否存在直线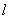 ,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线
,使得线段AB的垂直平分线经过圆心O2?若存在,求出直线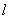 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
[解](Ⅰ)由已知,点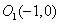 ,
,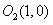 ,
,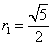 ,
,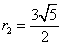 ,则
,则
|O1O2|=2<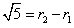 ,所以⊙O1内含于⊙O2.
(2分)
,所以⊙O1内含于⊙O2.
(2分)
设圆P的半径为r,因为动圆P与⊙O 1外切,且与⊙O2内切,则
1外切,且与⊙O2内切,则
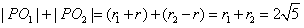 .
.
所以动圆圆心P轨迹是以点
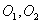 为焦点的椭圆.
(4分)
为焦点的椭圆.
(4分)
因为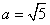 ,
,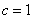 ,所以
,所以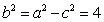 .
.
故动圆圆心P的轨迹方程是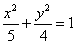 .
(6分)
.
(6分)
(Ⅱ)因为直线x=5与椭圆无交点,可设直线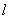 的方程为
的方程为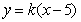 .
.
由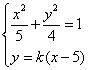 ,得
,得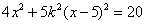 ,即
,即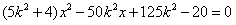 .(8分)
.(8分)
设点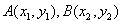 ,AB的中点为
,AB的中点为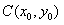 ,则
,则
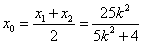 ,
,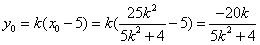 .
(10分)
.
(10分)
若线段AB的垂直平分线经过圆心O2,则CO2⊥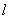 ,即
,即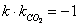 .
.
所以 ,即4=0,矛盾!
(12分)
,即4=0,矛盾!
(12分)
故不存在直线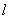 使得线段AB的垂直平分线经过圆心O2.
使得线段AB的垂直平分线经过圆心O2.
 (13分)
(13分)
19.(本小题满分13分)
据调查,湖南某地区有100万从事传统农业的农民,人均年收入3000元.为了增加农民的收入,当地政府积极引资建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作. 据估计,如果有x(x>0)万人进入企业工作,那么剩下从事传统农业的农民的人均年收入有望提高2x%,而进入企业工作的农民人均年收入为3000a元(a>0为常数).
(I)在建立加工企业后,要使该地区从事传统农业的农民的年总收入不低于加工企业建立前的年总收入,求x的取值范围;
(II)在(I)的条件下,当地政府应安排多少万农民进入加工企业工作,才能使这100万农民的人均年收入达到最大?
[解](I)据题意,(100-x)·3000·(1+2x%)≥100×3000, (2分)
即x2-50x≤0,解得0≤x≤50. (3分)
又x>0,故x的取值范围是(0,50]. (4分)
(II)设这100 万农民的人均年收入为y元,则
万农民的人均年收入为y元,则
y=100=100
=-5[x-25(a +1)]2+3000+475(a+1)2
+1)]2+3000+475(a+1)2  (0<x≤50).
(0<x≤50).
 (9分)
(9分)
(1)若0<25(a+1)≤50,即0<a≤1,则当x=25(a+1)时,y取最大值;
(2)若25(a+1)>50,即a >1,则当x=50时,y取最大值. (11分)
答:当0<a≤1时,安排25(a+1)万人进入加工企业工作,当a>1时,安排50万人进入企业工作,才能使这100万人的人均年收入最大. (13分)
18.(本小题满分12分)
如图,四边形ABCD是菱形,PA⊥平面ABCD,M为PA的中点.
(Ⅰ)求证:PC∥平面BDM;
(Ⅱ)若PA=AC=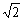 ,BD=
,BD= ,求直线BM与
,求直线BM与
平面PAC所成的角.
[解](Ⅰ)设AC与BD的交点为O,连结OM.
因为ABCD是菱形,则O为AC中点.
又M为PA的中点,所以OM∥PC. (3分)
因为OM在平面BDM内,所以PC∥平面BDM. (4分)
(Ⅱ)因为ABCD是菱形,则BD⊥AC.
又PA⊥平面ABCD,则PA⊥BD.
所以BD⊥平面PAC.
所以∠BMO是直线BM与平面PAC所成的角. (7分)
因为PA⊥平面ABCD,所以PA⊥AC. 在Rt△PAC中,因为PA=AC=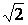 ,则PC=2.
,则PC=2.
又点M与点O分别是PA与AC的中点,则MO=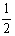 PC=1.
(9分)
PC=1.
(9分)
又BO=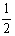 BD=
BD= ,在Rt△BOM中,tan∠BMO=
,在Rt△BOM中,tan∠BMO= ,所以∠BMO=60°.
,所以∠BMO=60°.
故直线BM与平面PAC所成的角是60°. (12分)
17.(本小题满分12分)
已知函数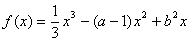 ,其中a,b为实常数.
,其中a,b为实常数.
(Ⅰ)求函数 为奇函数的充要条件;
为奇函数的充要条件;
(Ⅱ)若任取a∈[0,4],b∈[0,3],求函数 在R上是增函数的概率.
在R上是增函数的概率.
[解](Ⅰ)若 为奇函数,则对任意x∈R,
为奇函数,则对任意x∈R,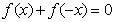 恒成立,即
恒成立,即
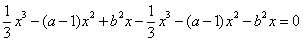 ,即
,即 恒成立,所以
恒成立,所以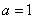 .(3分)
.(3分)
当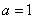 时,
时, ,则
,则 ,所以
,所以 为奇函数.(5分)
为奇函数.(5分)
故 为奇函数的充要条件是
为奇函数的充要条件是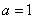 .
(6分)
.
(6分)
(Ⅱ)因为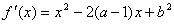 .
(7分)
.
(7分)
若 在R上是增函数,则对任意x∈R,
在R上是增函数,则对任意x∈R, 恒成立
恒成立
所以△=4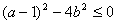 ,即
,即 .
(8分)
.
(8分)
设“ 在R上是增函数”为事件A,则事件A对应的区域为
在R上是增函数”为事件A,则事件A对应的区域为 .
.
又全部试验结果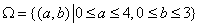 ,如图.
,如图.
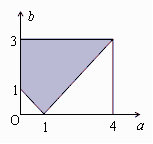 (10分)
(10分)
所以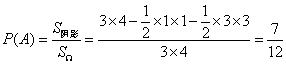 .
.
故函数 在R上是增函数的概率为
在R上是增函数的概率为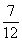 .
(12分)
.
(12分)
16.(本小题满分12分)
已知函数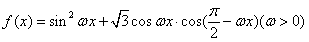 ,且函数
,且函数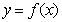 的图象相邻两条对称轴之间的距离为
的图象相邻两条对称轴之间的距离为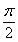 .
.
(Ⅰ)求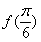 的值;
的值;
(Ⅱ)若函数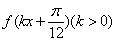 在区间
在区间 上单调递增,求k的取值范围.
上单调递增,求k的取值范围.
[解](Ⅰ)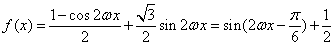 .
(2分)
.
(2分)
据题意,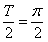 ,即
,即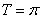 ,所以
,所以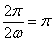 ,即
,即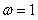 .
(4分)
.
(4分)
从而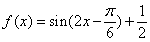 ,故
,故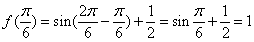 .
(6分)
.
(6分)
(Ⅱ)因为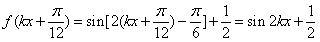 ,
,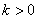 ,则
(8分)
,则
(8分)
当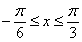 时,
时,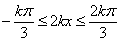 .
(9分)
.
(9分)
据题意,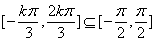 ,所以
,所以 ,解得
,解得 .
.
故k的取值范围是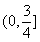 .
(12分)
.
(12分)
15.已知数列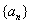 为等差数列.
为等差数列.
(1)若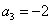 ,
,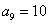 ,则
,则 16 ;
16 ;
(2)一般地,若 ,
, ,则
,则
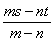 .
.
[解析](1)设等差数列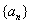 的公差为d,则
的公差为d,则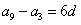 .由已知
.由已知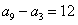 ,所以
,所以 .
.
故 .
.
(2)因为 ,则
,则 .
.
14.函数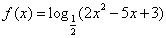 的单调递增区间是
的单调递增区间是 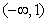 .
.
[解析]由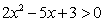 得
得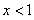 或
或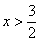 .
.
令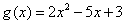 ,则当x<1时,
,则当x<1时,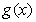 为减函数,当
为减函数,当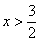 时,
时,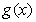 为增函数函数.
为增函数函数.
又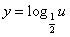 是减函数,故
是减函数,故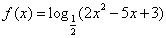 在
在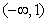 为增函数.
为增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com