
14、 ; 15、 。
三、解答题:本大题共6小题,满分80分.解答应写出文字说明、证明过程或演算步骤
12、 ; 13、 ;
(二)选做题(考生只需从14、15小题中任选一题作答)
二、填空题:本大题共6小题,其中14-15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分30分.
(一)必做题(11-13题)
9、 ; 10、 ; 11、 ;
(二)选做题(14 ~ 15题,考生只能从中选做一题)
 14. (坐标系与参数方程)曲线
14. (坐标系与参数方程)曲线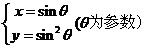 与直线
与直线 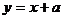 有两个公共点,则实数
有两个公共点,则实数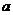 的取值范围是
.
的取值范围是
.
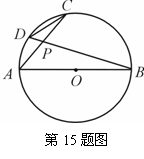
15.(几何证明选讲)如图,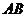 为⊙
为⊙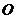 的直径,弦
的直径,弦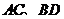 交
交
于点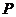 ,若
,若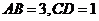 , 则
, 则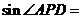 .
.
三、解答题:本大题共6小题,满分80分.解答应写出文字说明、证明过程或演算步骤
16.(本题满分12分)
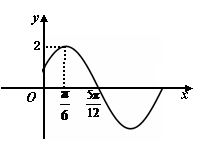
已知函数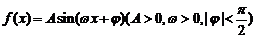 的部分图象如图所示.
的部分图象如图所示.
(Ⅰ)求函数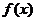 的解析式;
的解析式;
 (Ⅱ)令
(Ⅱ)令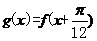 ,判断函数
,判断函数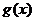 的奇偶性,并说明理由.
的奇偶性,并说明理由.
17.(本题满分12分)
2008年金融风暴横扫全球。为抗击金融风暴,市工贸系统决定对所属企业给予低息贷款的扶持.该系统先根据相关评分标准对各个企业进行了评估,并依据评估得分将这些企业分别评定为优秀、良好、合格、不合格4个等级,然后根据评估等级分配相应的低息贷款金额,其评估标准和贷款金额如下表:
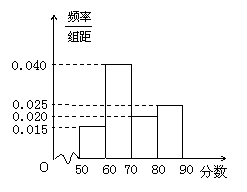
为了更好地掌控贷款总额,该系统随机抽查了所属部分企业的评估分数,得其频率分布直方图如下:
(Ⅰ)估计该系统所属企业评估得分的中位数;
 (Ⅱ)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?
(Ⅱ)该系统要求各企业对照评分标准进行整改,若整改后优秀企业数量不变,不合格企业、合格企业、良好企业的数量依次成等差数列,系统所属企业获得贷款的均值(即数学期望)不低于410万元,那么整改后不合格企业占企业总数的百分比的最大值是多少?
18.(本题满分14分)
已知四棱锥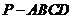 的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.
的三视图如下图所示,其中主视图、侧视图是直角三角形,俯视图是有一条对角线的正方形.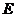 是侧棱
是侧棱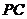 上的动点.
上的动点.
(Ⅰ)求证: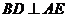
(Ⅱ) 若
若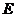 为
为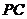 的中点,求直线
的中点,求直线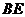 与平面
与平面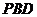 所成角的正弦值;
所成角的正弦值;
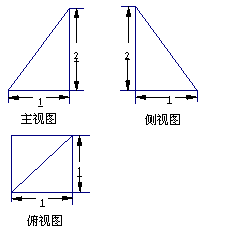
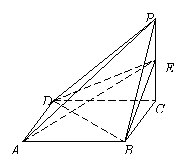 (Ⅲ)若五点
(Ⅲ)若五点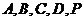 在同一球面上,求该球的体积.
在同一球面上,求该球的体积.
19. (本题满分14分)已知动点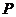 的轨迹为曲线
的轨迹为曲线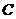 ,且动点
,且动点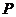 到两个定点
到两个定点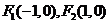 的距离
的距离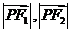 的等差中项为
的等差中项为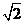 .
.
(Ⅰ)求曲线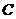 的方程;
的方程;
(Ⅱ)直线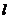 过圆
过圆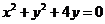 的圆心
的圆心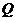 与曲线
与曲线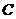 交于
交于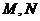 两点,且
两点,且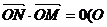 为坐标原点),求直线
为坐标原点),求直线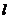 的方程;
的方程;
(Ⅲ)设点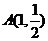 ,点
,点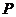 为曲线
为曲线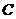 上任意一点,求
上任意一点,求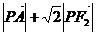 的最小值,并求取得最小值时点
的最小值,并求取得最小值时点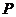 的坐标.
的坐标.
20. (本题满分14分)已知函数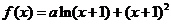 在
在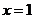 处有极值.
处有极值.
(Ⅰ)求实数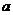 值;
值;
(Ⅱ)求函数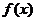 的单调区间;
的单调区间;
(Ⅲ)试问是否存在实数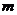 ,使得不等式
,使得不等式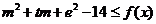 对任意
对任意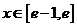 及
及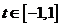 恒成立?若存在,求出
恒成立?若存在,求出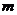 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.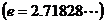
21.(本题满分14分)
已知数列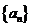 的首项为
的首项为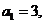 点
点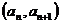 在直线
在直线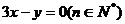 上.
上.
(Ⅰ)求数列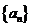 的通项公式;
的通项公式;
(Ⅱ)若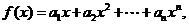 求
求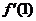 的值,并化简.
的值,并化简.
(Ⅲ)若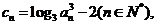 证明对任意的
证明对任意的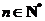 ,不等式
,不等式
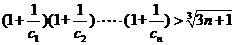 恒成立.
恒成立.
广东省2010届高三六校第四次联考
数学(理科)答题卷 20100206
(一)必做题(9-13题)
9.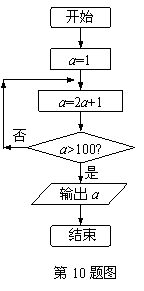 作用于同一点的两个力
作用于同一点的两个力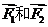 的夹角为
的夹角为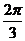 ,且
,且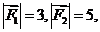 则
则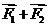 大小为
.
大小为
.
10.程序框图(即算法流程图)如右图所示,其输出结果是 .
11.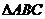 中,角
中,角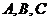 所对的边分别为
所对的边分别为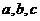 ,若
,若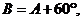
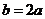 ,则
,则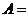 .
.
12. 二项式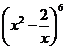 的展开式中
的展开式中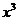 的系数是
(用数字作答)
的系数是
(用数字作答)
13. 设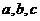 为正实数,且
为正实数,且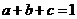 ,则
,则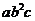 的最大值 为
.
的最大值 为
.
8. 有一种掷正方体骰子走跳棋的网络游戏,棋盘上标有第0站,第1站,第2站,…,第100站.一枚棋子开始在第0站,玩家每掷一次骰子,棋子向前跳动一次,若掷出朝上的点数为1或2,则棋子向前跳一站;若掷出其余点数,则棋子向前跳两站. 游戏规定:若棋子经过若干次跳动恰跳到第99站,则玩家获胜,游戏结束;若棋子经过若干次跳动最后恰跳到第100站,则玩家失败,游戏结束.设棋子跳到第n站的概率为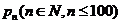 ,可以
,可以
证明: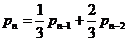 (2≤n≤100),则每次玩该游戏获胜的概率是
(2≤n≤100),则每次玩该游戏获胜的概率是
A.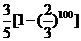 B.
B. 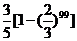 C.
C.
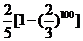 D.
D. 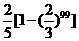
7. 已知函数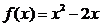 ,则满足条件
,则满足条件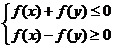 的点
的点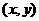 所在区域的面积为
所在区域的面积为
A.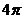 B.
B.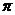 C.
C.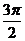 D.
D.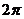
6. 平面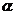 的斜线
的斜线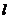 与平面
与平面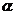 所成的角是
所成的角是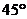 ,则直线
,则直线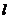 与平面
与平面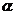 内所有不过斜足的直线所成的角中,最大的角是
内所有不过斜足的直线所成的角中,最大的角是
A.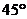 B.
B.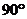 C.
C.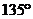 D.
D.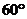


5.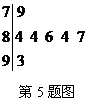 右图是2009年我校校园歌手大赛比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为
右图是2009年我校校园歌手大赛比赛现场上七位评委为某选手打出的分数的茎叶统计图,去掉一个最高分和一个最低分后,所剩数据的平均数为
A.83 B.84
C.85 D.86
3. 等差数列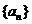 中,若
中,若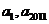 为方程
为方程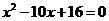 的两根,则
的两根,则 等于
等于
A.10 B.15 C.20 D.40
4. 设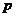 和
和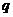 是两个简单命题,若
是两个简单命题,若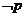 是
是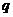 的充分不必要条件,则
的充分不必要条件,则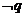 是
是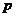 的
的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不充要条件
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com