
2.抛物线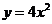 的焦点坐标为
的焦点坐标为
A.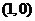 B.
B.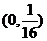 C.
C.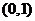 D.
D.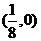
1.若复数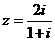 ,则
,则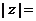
A.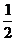 B.
B.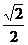 C.1 D.
C.1 D.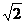
6.椭圆的参数方程的重要用途是设椭圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在椭圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系;如求椭圆上的点到一条直线的距离的最值。
[举例]若动点(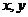 )在曲线
)在曲线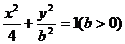 上变化,则
上变化,则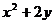 的最大值为 ( )
的最大值为 ( )
A.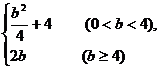 B.
B.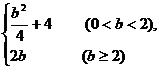
C.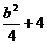 D.2
D.2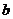
解析:本题可以直接借助于椭圆方程把x2用y表示,从而得到一个关于y 的二次函数,再配方求最值;这里用椭圆的参数方程求解:记x=2cos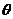 ,y=bsin
,y=bsin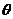 ,
, 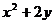 =4cos2
=4cos2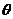 +
+
2bsin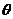 =f(
=f(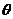 ),f(
),f(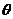 )=-4sin2
)=-4sin2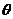 +2bsin
+2bsin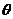 +4=-4(sin
+4=-4(sin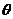 -
-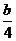 )2+
)2+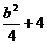 , sin
, sin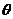 ∈[-1,1]
∈[-1,1]
若0<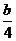 ≤1
≤1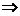 0<b≤4,则当sin
0<b≤4,则当sin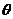 =
=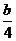 时f(
时f(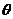 )取得最大值
)取得最大值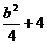 ;若
;若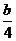 >1
>1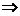 b>4,则当sin
b>4,则当sin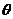 =1时f(
=1时f(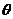 )取得最大值2
)取得最大值2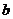 ,故选A
,故选A
[巩固]椭圆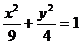 上的点到直线2x-
上的点到直线2x-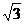 y+3
y+3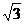 =0距离的最大值是_____________。
=0距离的最大值是_____________。
5.研究椭圆上一点与两焦点组成的三角形(焦点三角形)问题时,常用椭圆定义及正、余弦定理。
[举例]已知焦点在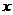 轴上的椭圆
轴上的椭圆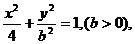 F1,F2是它的两个焦点,若椭圆上存在点P,使得
F1,F2是它的两个焦点,若椭圆上存在点P,使得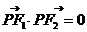 ,则
,则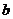 的取值范围是
。
的取值范围是
。
解析:思路一:先证一个结论:若B为椭圆短轴端点,则∠F1PF2≤∠F1BF2。记∠F1PF2=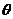 ,
,
|PF1|=r1, |PF2|=r2,cos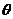 =
=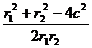 =
=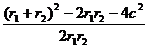 =
=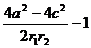
又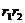 ≤(
≤(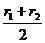 )2=
)2=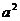 ,∴cos
,∴cos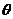 ≥
≥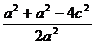 =cos∠F1BF2,当且仅当r1=r2时等号成立,
=cos∠F1BF2,当且仅当r1=r2时等号成立,
即∠F1PF2≤∠F1BF2。题中椭圆上存在点P,使得∠F1PF2=900,当且仅当∠F1BF2≥900,即
cos∠F1BO≤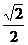
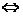 b≤
b≤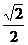 a=
a=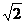 ,∴b∈(0,
,∴b∈(0, 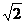
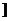 .思路二:用勾股定理:r1+r2=2a
①
.思路二:用勾股定理:r1+r2=2a
①
r12+r22=4c2 ②,由①②得:2r1r2=4b2,又2r1r2≤r12+r22 ∴b2≤c2=4-b2 即b∈(0, 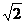
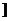 .
.
思路三:用向量的坐标运算:记P(x0,y0),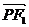 =(-c-x0,-y0),
=(-c-x0,-y0), 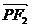 =(c-x0,-y0),
=(c-x0,-y0),
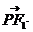
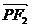 =c2-x02+y02=0
=c2-x02+y02=0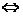 (b2+4)x02=4(c2-b2),注意到:0≤x02≤4,∴0≤4(c2-b2)≤4(b2+4)
(b2+4)x02=4(c2-b2),注意到:0≤x02≤4,∴0≤4(c2-b2)≤4(b2+4)
即0≤4-2b2≤b2+4,得b∈(0, 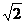
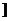 .
.
[巩固1]椭圆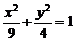 的焦点为
的焦点为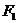 、
、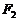 ,点P为其上的动点,当
,点P为其上的动点,当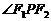 为钝角时,点P横坐标的取值范围是________。
为钝角时,点P横坐标的取值范围是________。
[巩固2]已知P是椭圆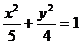 上一点,F1和F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
上一点,F1和F2是焦点,若∠F1PF2=30°,则△PF1F2的面积为( )
A.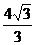 B.
B.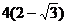 C.
C.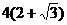 D.4
D.4
4.研究椭圆上的点到其焦点的距离问题时,往往用定义;会推导并记住椭圆的焦半径公式。
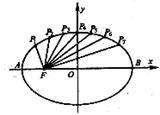 [举例1] 如图把椭圆
[举例1] 如图把椭圆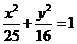 的长轴AB分成8分,过
的长轴AB分成8分,过
每个分点作x轴的垂线交椭圆的上半部分于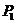 ,
,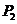 ,……
,……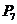
七个点,F是椭圆的一个焦点,则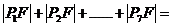 ____________.
____________.
解析:P1与P7,P2与P6,P3与P5关于y轴对称,P4在y轴上,
记椭圆的另一个焦点为F/,则|P7F|=|P1F/|,|P6F|=|P2F/|,|P5F|=|P3F/|,
于是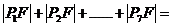 |P1F|+|P1F/|+|P2F|+|P2F/|+|P3F|+|P3F/|+|P4F|=7a=35.
|P1F|+|P1F/|+|P2F|+|P2F/|+|P3F|+|P3F/|+|P4F|=7a=35.
[举例2] 已知A、B是椭圆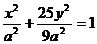 上的两点,F2是椭圆的右焦点,如果
上的两点,F2是椭圆的右焦点,如果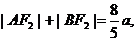 AB的中点到椭圆左准线距离为
AB的中点到椭圆左准线距离为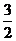 ,则椭圆的方程 .
,则椭圆的方程 .
解析: 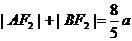
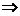
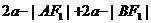 =
=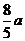
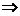
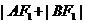 =
=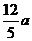 ,
,
记AB的中点为M ,A、B、M在椭圆左准线上的射影分别为A1、B1,M1,由椭圆第二定义知:|AF1|=e|AA1|,|BF1|=e|BB1|,于是有:e(|AA1|+|BB1|)=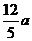 ,而e=
,而e=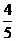
∴|AA1|+|BB1|=3a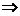 2|MM1|=3a,又|MM1|=
2|MM1|=3a,又|MM1|=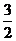 ,得a=1,故椭圆方程为
,得a=1,故椭圆方程为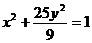 。
。
[巩固1] 椭圆的两焦点为F1,F2,以F1F2为一边的正三角形的另两条边均被椭圆平分,则椭圆的离心率为 。
[巩固2]已知F1、F2是椭圆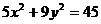 的左右焦点,点
的左右焦点,点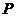 是此椭圆上的一个动点,
是此椭圆上的一个动点,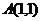 为一个定点,则
为一个定点,则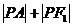 的最大值为
,
的最大值为
,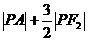 的最小值为
。
的最小值为
。
[提高] 过椭圆左焦点F且斜率为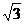 的直线交椭圆于A、B两点,若|FA|=2|FB|,则椭圆的离心率e=_____
的直线交椭圆于A、B两点,若|FA|=2|FB|,则椭圆的离心率e=_____
3.圆锥曲线的定义是求轨迹方程的重要载体之一。
[举例1]已知⊙Q:(x-1)2+y2=16,动⊙M过定点P(-1,0)且与⊙Q相切,则M点的轨迹方程是:
。
解析:P(-1,0)在⊙Q内,故⊙M与⊙Q内切,记:M(x,y),⊙M的半径是为r,则:
|MQ|=4-r,又⊙M过点P,∴|MP|=r,于是有:|MQ|=4-|MP|,即|MQ|+|MP|=4,可见M点的轨迹是以P、Q为焦点(c=1)的椭圆,a=2。
[举例2] 若动点P(x,y)满足|x+2y-3|=5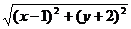 ,则P点的轨迹是:
,则P点的轨迹是:
A.圆 B、椭圆 C、双曲线 D、抛物线
解析:等式两边平方,化简方程是最容易想到的,但不可行,一方面运算量很大,另一方面是平方、展开后方程中会出现xy项,这就给我们判断曲线类型带来了麻烦。但是,仔细观察方程后,就会发现等式左边很“象”是点到直线的距离,而等式右边则是两点间的距离的5倍;为了让等式左边变成点到直线的距离,可以两边同除以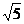 ,于是有:
,于是有:
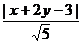 =
=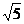
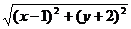 ,这就已经很容易联想到圆锥曲线的第二定义了,
,这就已经很容易联想到圆锥曲线的第二定义了,
只需将方程再变形为: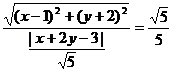 ,即动点P(x,y)到定点A(1,2)与到定直线x+2y-3=0的距离之比为
,即动点P(x,y)到定点A(1,2)与到定直线x+2y-3=0的距离之比为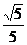 ,∴其轨迹为椭圆。
,∴其轨迹为椭圆。
[巩固1] 已知圆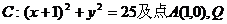 为圆上一点,AQ的垂直平分线交CQ于M,则点M的轨迹方程为
.
为圆上一点,AQ的垂直平分线交CQ于M,则点M的轨迹方程为
.
[巩固2]设x、y∈R,在直角坐标平面内,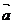 =(x,y+2),
=(x,y+2),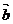 =(x,y-2),且|
=(x,y-2),且|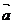 |+|
|+|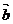 |=8,则点
|=8,则点
M(x,y)的轨迹方程为 。
[提高]已知A(0,7),B(O,-7),C(12,2),以C为一个焦点作过A、B的椭圆,则椭圆的另一焦点的轨迹方程为 。
[迁移] P为直线x-y+2=0上任一点,一椭圆的两焦点为F1(-1,0)、F2(1,0),则椭圆过P点且长轴最短时的方程为 。
2.椭圆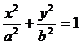 关于x轴、y轴、原点对称;P(x,y)是椭圆上一点,则|x|≤a,|y|≤b,
关于x轴、y轴、原点对称;P(x,y)是椭圆上一点,则|x|≤a,|y|≤b,
a-c≤|PF|≤a+c,(其中F是椭圆的一个焦点),椭圆的焦点到短轴端点的距离为a,椭圆的焦准距为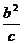 ,椭圆的通经(过焦点且垂直于长轴的弦)长为2
,椭圆的通经(过焦点且垂直于长轴的弦)长为2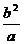 ,通经是过焦点最短的弦。
,通经是过焦点最短的弦。
[举例1] 已知椭圆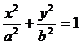 (
(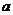 >0,
>0,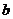 >0)的左焦点为F,右顶点为A,上顶点为B,若
>0)的左焦点为F,右顶点为A,上顶点为B,若
BF⊥BA,则称其为“优美椭圆”,那么“优美椭圆”的离心率为 。
解析:|AB|2=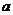 2+
2+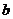 2,|BF|=
2,|BF|=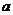 ,|FA|=
,|FA|=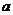 +
+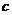 ,在Rt⊿ABF中,(
,在Rt⊿ABF中,(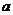 +
+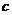 )2=
)2=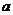 2+
2+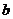 2+
2+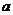 2
2
化简得: 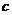 2+
2+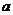
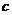 -
-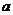 2=0,等式两边同除以
2=0,等式两边同除以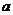 2得:
2得: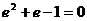 ,解得:
,解得: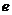 =
=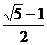 。
。
注:关于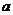 ,
,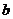 ,
,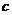 的齐次方程是“孕育”离心率的温床。
的齐次方程是“孕育”离心率的温床。
[举例2] 已知椭圆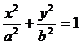 (
(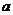 >0,
>0,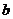 >0)的离心率为
>0)的离心率为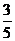 ,若将这个椭圆绕着它的右焦点按逆时针方向旋转
,若将这个椭圆绕着它的右焦点按逆时针方向旋转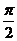 后,所得的新的椭圆的一条准线的方程为
后,所得的新的椭圆的一条准线的方程为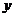 =
=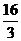 ,则原来椭圆的方程是
。
,则原来椭圆的方程是
。
解析:原来椭圆的右焦点为新椭圆的上焦点,在x轴上,直线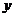 =
=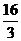 为新椭圆的上准线,故新椭圆的焦准距为
为新椭圆的上准线,故新椭圆的焦准距为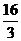 ,∴原来椭圆的焦准距也为
,∴原来椭圆的焦准距也为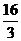 ,于是有:
,于是有: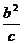 =
=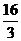 ①,
①,
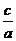 =
=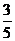 ②,由①②解得:
②,由①②解得: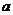 =5,
=5,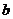 =3。
=3。
[巩固1]一椭圆的四个顶点为A1,A2,B1,B2,以椭圆的中心为圆心的圆过椭圆的焦点,的椭圆的离心率为 。
[巩固2] 在给定椭圆中,过焦点且垂直于长轴的弦长为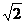 ,焦点到相应准线的距离为1,则该椭圆的离心率为
,焦点到相应准线的距离为1,则该椭圆的离心率为
(A)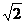 (B)
(B)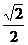 (C)
(C) 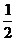 (D)
(D)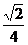
[迁移]椭圆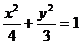 上有n个不同的点P1,P2,P3,…,Pn,椭圆的右焦点F,数列{| PnF|}
上有n个不同的点P1,P2,P3,…,Pn,椭圆的右焦点F,数列{| PnF|}
是公差大于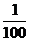 的等差数列,则n的最大值为
( )
的等差数列,则n的最大值为
( )
A.198 B.199 C.200 D.201
1.方程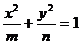 表示椭圆
表示椭圆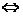
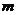 >0,
>0,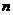 >0,且
>0,且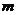 ≠
≠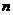 ;
;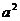 是
是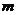 ,
,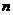 中之较大者,焦点的位置也取决于
中之较大者,焦点的位置也取决于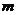 ,
,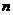 的大小。
的大小。
[举例] 椭圆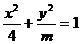 的离心率为
的离心率为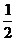 ,则
,则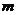 =
=
解析:方程中4和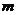 哪个大哪个就是
哪个大哪个就是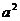 ,因此要讨论;(ⅰ)若0<
,因此要讨论;(ⅰ)若0<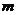 <4,则
<4,则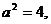
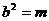 ,∴
,∴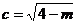 ,∴
,∴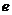 =
=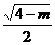 =
=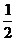 ,得
,得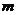 =3;(ⅱ)
=3;(ⅱ)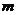 >4,则
>4,则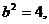
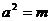 ,∴
,∴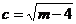 ,∴
,∴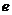 =
=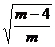 =
=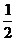 ,得
,得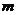 =
=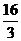 ;综上:
;综上: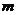 =3或
=3或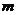 =
=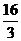 。
。
[巩固]若方程:x2+ay2=a2 表示长轴长是短轴长的2倍的椭圆,则a的允许值的个数是
A 1个 B .2个 C.4个 D.无数个
5.圆的参数方程的本质是sin2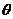 + cos2
+ cos2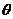 =1。参数方程的重要用途是设圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系。
=1。参数方程的重要用途是设圆上一点的坐标时,可以减少一个变量,或者说坐标本身就已经体现出点在圆上的特点了,而无需再借助圆的方程来体现横纵坐标之间的关系。
[举例]已知圆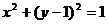 上任意一点P(x、y)都使不等式x+y+m³0成立,则m的取值范围是:A .[
上任意一点P(x、y)都使不等式x+y+m³0成立,则m的取值范围是:A .[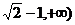 B
B 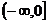 C (
C (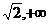 )
D
)
D 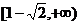 ( )
( )
解析:不等式x+y+m³0恒成立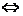 m³ -(x+y)恒成立,以下求-(x+y)的最大值:
m³ -(x+y)恒成立,以下求-(x+y)的最大值:
记x= cos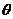 、y=1+
sin
、y=1+
sin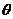 ,-(x+y)= -( cos
,-(x+y)= -( cos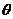 +1+ sin
+1+ sin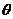 )= -1-
)= -1-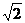 sin(
sin(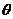 +
+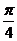 )≤-1+
)≤-1+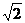 ,选A。
,选A。
[巩固1] 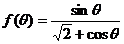 的最大值为
。
的最大值为
。
[巩固2]在⊿ABC中,已知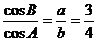 ,c=10,P是⊿ABC的内切圆上一点,则PA2+PB2
,c=10,P是⊿ABC的内切圆上一点,则PA2+PB2
+PC2的最大值为
[迁移]动点P,Q坐标分别为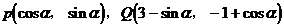 ,(
,(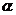 是参数),则|PQ|的最大值与最小值的和为 .
是参数),则|PQ|的最大值与最小值的和为 .
4.判断两圆的位置关系用圆心距与它们半径和、差的大小。⊙M、⊙N的半径分别为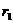 、
、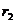 ,
,
|MN|>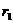 +
+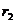
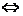 外离,|MN|=
外离,|MN|=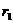 +
+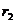
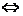 外切,|
外切,|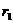 -
-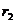 |<|MN|<
|<|MN|<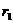 +
+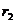
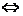 相交,此时,若⊙M:
相交,此时,若⊙M:
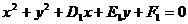 ,⊙N:
,⊙N: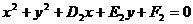 ,过两圆交点的圆(系)的方程为:
,过两圆交点的圆(系)的方程为: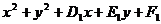 +
+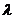 (
(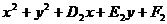 )=0(⊙N除外)。
)=0(⊙N除外)。
特别地:当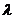 = -1时,该方程表示两圆的公共弦。连心线垂直平分公共弦。|MN|=|
= -1时,该方程表示两圆的公共弦。连心线垂直平分公共弦。|MN|=|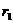 -
-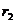 |
|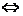 内切,|MN|<|
内切,|MN|<|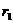 -
-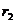 |
| 内含。
内含。
[举例1]已知两圆O1:x2+y2=16,O2:(x-1)2+(y+2)2=9,两圆公共弦交直线O1O2于M点,则O1分有向线段MO2所成的比λ= ( )
A.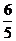 B.
B.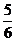 C.-
C.-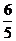 D.-
D.-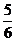
解析:直线O1 O2:y= -2x,两圆公共弦:x-2y=6,于是有:M(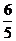 ,
,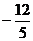 ),有定比分点坐标公式不难得到λ的值,选C。
),有定比分点坐标公式不难得到λ的值,选C。
[举例2] 若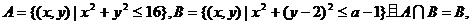
则a的取值范围是 ( )
A.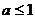 B.
B.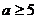 C.
C.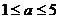 D.
D.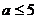
解析:集合A、B分别表示两个圆面(a=1时集B表示一个点),A∩B=B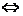 B
B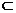 A,即两圆内含;有两圆圆心分别为原点和(0,2),半径分别为4和
A,即两圆内含;有两圆圆心分别为原点和(0,2),半径分别为4和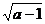 ,于是有:2≤4-
,于是有:2≤4-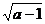 ,解得:
,解得: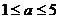 ,选C。
,选C。
[巩固1]圆心在直线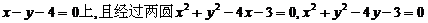 的交点的圆的方程为 ( )
的交点的圆的方程为 ( )
A.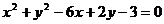 B.
B.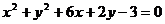
C.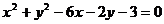 D.
D.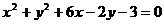
[巩固2]若圆(x-a)2+(y-b)2=6始终平分圆x2+y2+2x+2y-3=0的周长,则动点M(a,b)的轨迹方程是
A.a2+b2-2a-2b+1=0 B.a2+b2+2a+2b+1=0
C.a2+b2-2a+2b+1=0 D.a2+b2+2a-2b+1=0
[迁移]与圆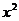 +
+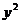
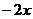 =0外切且与
=0外切且与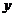 轴相切的动圆圆心的轨迹方程为
。
轴相切的动圆圆心的轨迹方程为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com