
2.公式的变用:
1+cos2α= ;
1-cos2α= .
|
例1. 求值: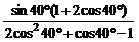
解:原式=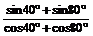
=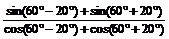 =
=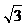
变式训练1: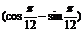 (cos
(cos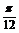 +sin
+sin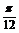 )= ( )
)= ( )
A.-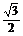 B.-
B.-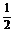 C.
C. 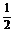 D.
D.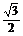
解:D
例2. 已知α为锐角,且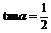 ,求
,求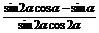 的值.
的值.
解:∵α为锐角
∴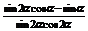 =
=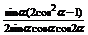
=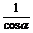 =
= =
=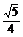
变式训练2:化简: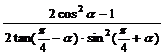
解:原式=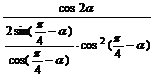 =1
=1
例3.已知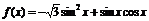 ;
;
(1) 求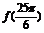 的值; (2) 设
的值; (2) 设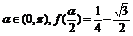 ,求sinα的值.
,求sinα的值.
解:(1)∵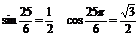
∴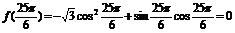
(2)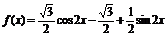
∴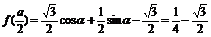
16sin22-4sinα-11=0
解得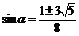
∵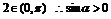 故
故
变式训练3:已知sin(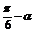 )=
)=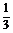 ,求cos(
,求cos(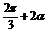 )的值.
)的值.
解:cos(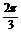 +2α)=2cos2(
+2α)=2cos2( +α)-1
+α)-1
=2sin2( -α) -1=-
-α) -1=-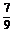
例4.已知sin2 2α+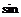 2α cosα-cos2α=1,α
2α cosα-cos2α=1,α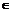 (0,
(0,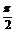 ),求sinα、tanα的值.
),求sinα、tanα的值.
解:由已知得
sin22α+sin2αcosα-2cos2α=0
即(sin2α+2cosα) (sin2α-cosα)=0
cos2α(1+sinα) (2sinα-1)=0
∵ α∈(0,
α∈(0,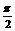 ) cosα≠0 sinα≠-1
) cosα≠0 sinα≠-1
∴2sinα=1 sinα=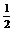 ∴tanα=
∴tanα=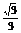
变式训练4:已知α、β、r是公比为2的等比数列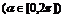 ,且sinα、sinβ、sinr也成等比数列,求α、β、r的值.
,且sinα、sinβ、sinr也成等比数列,求α、β、r的值.
解:∵α、β、r成公比为2的等比数列.
∴β=2α,r=4α
∵sinα、sinβ、sinr成等比数列
∴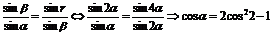
即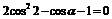 ,解得cosα=1或
,解得cosα=1或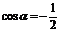
当cosα=1时,sinα=0与等比数列首项不为零矛盾故cosα=1舍去
当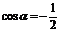 时,∵2∈[0,2π]
∴
时,∵2∈[0,2π]
∴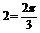 或
或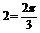
∴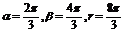 或
或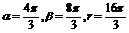
|
1.基本公式:
sin2α= ;
cos2α= = = ;
tan2α= .
2.在应用过程中要能灵活运用公式,并注意总结公式的应用经验。对一些公式不仅会正用,还要会逆用、变形用,如正切的和角公式的变形用,正、余弦的和、差角公式的逆用。另外还要能对形如sinx±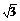 cosx、sinx±cosx的三角函数式要创造条件使用公式.
cosx、sinx±cosx的三角函数式要创造条件使用公式.
第4课时 二倍角的正弦、余弦、正切
|
1.三角函数式的化简、求值、证明等是三角变形常见的题型,三角函数式变形的过程就是分析矛盾、发现差异,进而消除差异的过程。在这一过程中须仔细观察到式子中各项的角、函数名称及运算式子的差异,找出特征,从中找到解题的突破口。对于角与角之间的关系,要充分应用角的恒等变换,以整体角来处理和解决有关问题,这样可以避免一些较复杂的计算,如:2α+β=α+ (α+β)等.
4.常见的角的变换:
2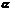 =(α+β)+(α-β);α=
=(α+β)+(α-β);α=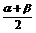 +
+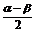
α=(α+β)-β =(α-β)+β
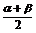 =(α-
=(α- )-(
)-( -β);
-β);
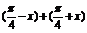 =
=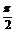
|
例1.求[2sin50°+sin10°(1+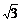 tan10°)]·
tan10°)]· 的值.
的值.
解:原式=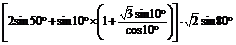
=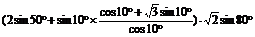
=
=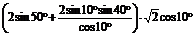
=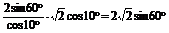
=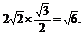
变式训练1:(1)已知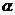 ∈(
∈(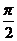 ,
,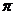 ),sin
),sin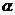 =
=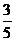 ,则tan(
,则tan(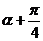 )等于( )
)等于( )
A.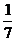 B.7
C.-
B.7
C.- 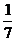 D.-7
D.-7
(2) sin163°sin223°+sin253°sin313°等于 ( )
A.-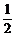 B.
B.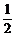 C.-
C.-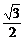 D.
D.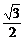
解:(1)A (2)B
例2. 已知α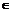 (
(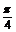 ,
,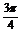 ),β
),β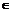 (0,
(0,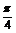 ),
),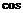 (α-
(α-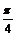 )=
)=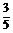 ,sin(
,sin(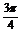 +β)=
+β)=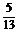 ,求sin(α+β)的值.
,求sin(α+β)的值.
解:∵α-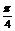 +
+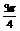 +β=α+β+
+β=α+β+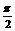
α∈(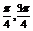 ) β∈(0,
) β∈(0, )
)
∴α-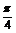 ∈(0,
∈(0,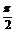 ) β+
) β+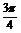 ∈(
∈(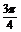 ,π)
,π)
∴sin(α-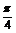 )=
)=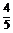 cos(
cos(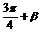 )=-
)=-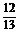
∴sin(α+β)=-cos[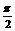 +(α+β)]
+(α+β)]
=-cos[(α-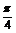 )+(
)+(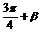 )]=
)]=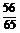
变式训练2:设cos(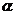 -
- )=-
)=-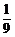 ,sin(
,sin(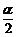 -β)=
-β)=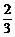 ,且
,且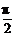 <
<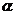 <π,0<β<
<π,0<β<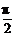 ,
,
求cos(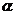 +β).
+β).
解:∵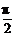 <
<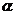 <π,0<β<
<π,0<β<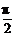 ,∴
,∴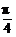 <α-
<α- <π,-
<π,-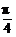 <
<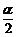 -β<
-β<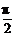 .
.
故由cos(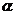 -
- )=-
)=-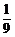 ,得sin(α-
,得sin(α- )=
)=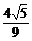 .
.
由sin(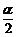 -β)=
-β)=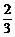 ,得cos(
,得cos(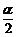 -β)=
-β)=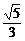 .∴cos
.∴cos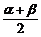 =cos[(
=cos[(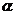 -
- )-(
)-(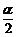 -β)]=
-β)]=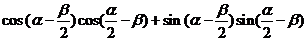 =
=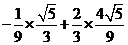
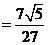 ∴cos(
∴cos(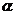 +β)=2cos2
+β)=2cos2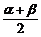 -1=
-1=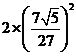 -1=-
-1=-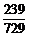 .
.
例3.
若sinA=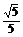 ,sinB=
,sinB=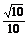 ,且A,B均为钝角,求A+B的值.
,且A,B均为钝角,求A+B的值.
解 ∵A、B均为钝角且sinA=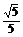 ,sinB=
,sinB=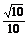 ,
,
∴cosA=-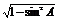 =-
=- =-
=-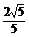 ,
,
cosB=-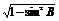 =-
=-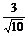 =-
=-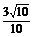 ,
,
∴cos(A+B)=cosAcosB-sinAsinB
=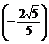 ×
× -
- ×
×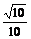 =
=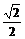 ①
①
又∵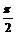 <A<
<A< ,
, 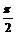 <B<
<B< ,
,
∴ <A+B<2
<A+B<2 ②
②
由①②知,A+B=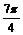 .
.
变式训练3:在△ABC中,角A、B 、C满足4sin2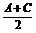 -cos2B=
-cos2B= ,求角B的度数.
,求角B的度数.
 解 在△ABC中,A+B+C=180°,
解 在△ABC中,A+B+C=180°,
由4sin2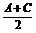 -cos2B=
-cos2B= ,
,
得4·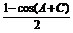 -2cos2B+1=
-2cos2B+1= ,
,
所以4cos2B-4cosB+1=0.
于是cosB=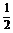 ,B=60°.
,B=60°.
例4.化简sin2 ·sin2
·sin2 +cos2
+cos2 cos2
cos2 -
- cos2
cos2 ·cos2
·cos2 .
.
解 方法一 (复角→单角,从“角”入手)
原式=sin2 ·sin2
·sin2 +cos2
+cos2 ·cos2
·cos2 -
- ·(2cos2
·(2cos2 -1)·(2cos2
-1)·(2cos2 -1)
-1)
=sin2 ·sin2
·sin2 +cos2
+cos2 ·cos2
·cos2 -
- (4cos2
(4cos2 ·cos2
·cos2 -2cos2
-2cos2 -2cos2
-2cos2 +1)
+1)
=sin2 ·sin2
·sin2 -cos2
-cos2 ·cos2
·cos2 +cos2
+cos2 +cos2
+cos2 -
-
=sin2 ·sin2
·sin2 +cos2
+cos2 ·sin2
·sin2 +cos2
+cos2 -
-
=sin2 +cos2
+cos2 -
- =1-
=1- =
= .
.
方法二 (从“名”入手,异名化同名)
原式=sin2 ·sin2
·sin2 +(1-sin2
+(1-sin2 )·cos2
)·cos2 -
- cos2
cos2 ·cos2
·cos2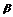
=cos2 -sin2
-sin2 (cos2
(cos2 -sin2
-sin2 )-
)- cos2
cos2 ·cos2
·cos2
=cos2 -sin2
-sin2 ·cos2
·cos2 -
- cos2
cos2 ·cos2
·cos2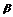
=cos2 -cos2
-cos2 ·
·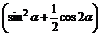
= -cos2
-cos2 ·
·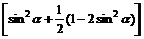
= -
- cos2
cos2 =
= .
.
方法三 (从“幂”入手,利用降幂公式先降次)
原式=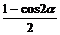 ·
·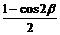 +
+ ·
·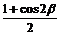 -
- cos2
cos2 ·cos2
·cos2
=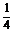 (1+cos2
(1+cos2 ·cos2
·cos2 -cos2
-cos2 -cos2
-cos2 )+
)+ (1+cos2
(1+cos2 ·cos2
·cos2 +cos2
+cos2 +cos2
+cos2 )-
)- ·cos2
·cos2 ·cos2
·cos2 =
= .
.
方法四 (从“形”入手,利用配方法,先对二次项配方)
原式=(sin ·sin
·sin -cos
-cos ·cos
·cos )2+2sin
)2+2sin ·sin
·sin ·cos
·cos ·cos
·cos -
- cos2
cos2 ·cos2
·cos2
=cos2( +
+ )+
)+ sin2
sin2 ·sin2
·sin2 -
- cos2
cos2 ·cos2
·cos2
=cos2( +
+ )-
)- ·cos(2
·cos(2 +2
+2 )
)
=cos2( +
+ )-
)-  ·[2cos2(
·[2cos2( +
+ )-1]=
)-1]= .
.
变式训练4:化简:(1) sin
sin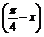 +
+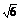 cos
cos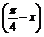 ;
;
(2)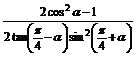 .
.
解 (1)原式=2
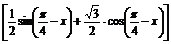
=2
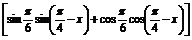
=2 cos
cos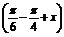 =2
=2 cos(x-
cos(x-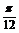 ).
).
(2)原式=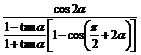 =
=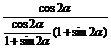 =1.
=1.
|
3.公式的变式
tanα+tanβ=tan (α+β)(1-tanα tanβ)
1-tanα tanβ=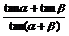
2.基本公式
sin(α±β)=sinα cosβ±cosα sinβ
cos(α±β)= ;
tan(α±β)= .
1.两角和的余弦公式的推导方法:
2.求函数的值域没有通用方法和固定模式,除了掌握常用方法(如直接法、单调性法、有界性法、配方法、换元法、判别式法、不等式法、图象法)外,应根据问题的不同特点,综合而灵活地选择方法.
第3课时 两角和与差的三角函数
|
1.求函数的定义域一般有三类问题:一是给出解释式(如例1),应抓住使整个解式有意义的自变量的集合;二是未给出解析式(如例2),就应抓住内函数的值域就是外函数的定义域;三是实际问题,此时函数的定义域除使解析式有意义外,还应使实际问题或几何问题有意义.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com