
3.求值常用的方法:切割化弦法、升幂降幂法、辅助元素法、“1”的代换法等.
第6课时  三角函数的恒等变形
三角函数的恒等变形
|
|||
|
|||
2.要熟悉角的拆拼、变换的技巧,倍角与半角的相对性,熟悉几种常见的入手方式:
① 变换角度
② 变换函数名
③ 变换解析式结构
1.三角函数的化简与求值的难点在于:众多的公式的灵活运用和解题突破口的选择,认真分析所给式子的整体结构,分析各个三角函数及角的相互关系是灵活选用公式的基础,是恰当寻找解题思维起点的关键所在;
4.反三角函数arcsinα、arccosα、arctanα分别表示[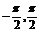 ]、[0,π]、(
]、[0,π]、(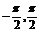 )的角.
)的角.
|
例1. (1)化简: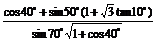
(2)化简: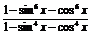
解:∵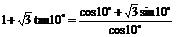
=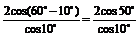 ∴原式
∴原式
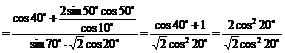 =
=
变式训练1:已知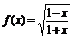 ,若
,若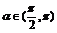 ,则
,则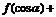
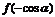 可化简为
.
可化简为
.
解: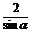
例2. 已知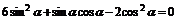 ,α∈[
,α∈[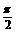 ,
,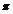 ],求
],求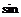 (2α+
(2α+ )的值.
)的值.
解法一:由已知得(3sinα+2cosα) (2sinα-cosα)=0
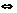 3sinα+2cosα=0或2sinα-cosα=0
3sinα+2cosα=0或2sinα-cosα=0
由已知条件可知cosα≠0 ∴α≠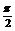 即α∈(
即α∈(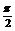 ,π)
,π)
∴tanα=-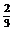
sin(2α+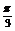 )=sin2αcos
)=sin2αcos +cos2αsin
+cos2αsin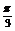
=sinαcosα+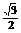 (cos2α-sin2α)
(cos2α-sin2α)
=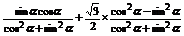
=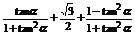
=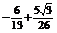
解法二:由已知条件可知cosα≠0 则α≠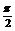
从而条件可化为 6 tan2α+tanα-2=0
∵α∈(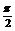 ,π) 解得tanα=-
,π) 解得tanα=-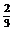 (下同解法一)
(下同解法一)
变式训练2:在△ABC中, ,
,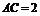 ,
,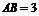 ,求
,求 A的值和△ABC的面积.
A的值和△ABC的面积.
解:∵sinA+cosA=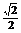 ①
①
∵2sinAcosA=-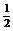
从而cosA<0 A∈(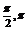 )
)
∴sinA-cosA=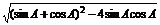
=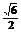 ②
②
据①②可得 sinA=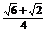 cosA=
cosA=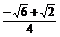
∴tanA=-2-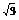
S△ABC=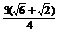
例3. 已知tan(α-β)=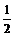 ,
,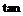 β=-
β=-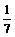 ,且α、β∈(0,
,且α、β∈(0, ),求2α-β的值.
),求2α-β的值.
解:由tanβ=-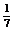 β∈(0,π)
β∈(0,π)
得β∈(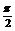 , π)
①
, π)
①
由tanα=tan[(α-β)+β]=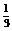 α∈(0,π)
α∈(0,π)
得0<α<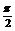 ∴ 0<2α<π
∴ 0<2α<π
由tan2α=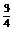 >0 ∴知0<2α<
>0 ∴知0<2α<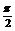
 ②
②
∵tan(2α-β)=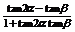 =1
=1
由①②知 2α-β∈(-π,0)
∴2α-β=-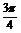
(或利用2α-β=2(α-β)+β求解)
变式训练3:已知α为第二象限角,且sinα=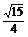 ,求
,求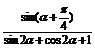 的值.
的值.
解:由sinα=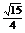 α为第二象限角
α为第二象限角
∴cosα=-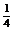
∴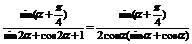
=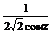 =-
=-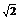
例4.已知 .
.
(1)求tanα的值;
(2)求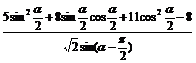 的值.
的值.
解:(1)由
得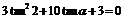 解得tanα=-3或
解得tanα=-3或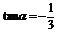
又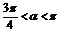 ,所以
,所以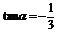 为所求.
为所求.
(2)原式: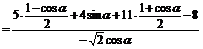
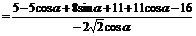
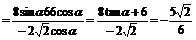
变式训练4:已知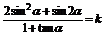 (
(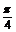 <α<
<α<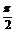 ),试用k表示sin
),试用k表示sin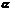 -cos
-cos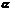 的值.
的值.
解:∵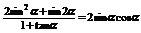
∴k=2sinαcosα
∵(sinα-cosα)2=1-k
又∵α∈(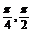 ) ∴sinα-cosα=
) ∴sinα-cosα=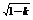
|
3.求值问题的基本类型及方法
① “给角求值”一般所给的角都是非特殊角,解题时应该仔细观察非特殊角与特殊角之间的关系,通常是将非特殊角转化为特殊角或相互抵消等方法进行求解.
② “给值求值”即给出某些角的三角函数(式)的值,求另外的一些角的三角函数值,解题关键在于:变角,使其角相同;
③ “给值求角”关键也是:变角,把所求的角用含已知角的式子表示,由所求得的函数值结合该函数的单调区间求得角.
2.常用的基本变换方法有:异角化同角、异名化同名、异次化同次.
1.三角函数式的化简的一般要求:
① 函数名称尽可能少;
② 项数尽可能少;
③ 尽可能不含根式;
④ 次数尽可能低、尽可能求出值.
3.对三角函数式的变形有以下常用的方法:
① 降次(常用降次公式)
② 消元(化同名或同角的三角函数)
③ 消去常数“1”或用“1”替换
④ 角的范围的确定
|
2.要理解二倍角的相对性,能根据公式的特点进行灵活应用(正用、逆用、变形用).
1.二倍角公式是和角公式的特殊情况,在学习时要注意它们之间的联系;
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com