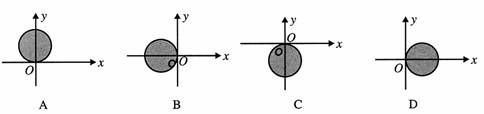
6．已知向量关于x轴对称，的点Z(x，y)的集合用阴影表示为　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

5．在等比数列其前n项的和积为等于

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．±2　　　　　　　　　　 B．±4　　　　　　　　　　 C．2　　　　　　　　　　　　 D．4

4．已知圆的方程为设该圆中过点(3，5)的最长弦和最短弦分别为AC和BD，则四边形ABCD的面积是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　　　　 B．　　　　　　　 C．　　　　　　　　 D．

3．若则角θ的终边一定落在直线(　　 )上

　　　 A．　　　　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　　　　 D．

2．在数列等于　　　　　　　　　 (　　 )

　　　 A．1　　　　　　　　　　　　 B．-1　　　　　　　　　　　 C．　　　　　　　　　　　 D．2

1．集合，则下列结论正确的是　　　　 (　　 )

　　　 A．　　　　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　　　　 D．

22．(本题15分).

(Ⅰ)由，得；又有且仅有一个解,即有唯一解满足.

当时，，则，此时

又当时，，因为，

所以，则，此时

综上所述，或者；　　　　　　　　　　　　　　　 4分

(Ⅱ) ，当时，，不合题意，

则，则，　 4分

(Ⅲ)由(Ⅱ)知，

则，所以　　　　　　 　　2分

设数列的前项和为，则

当时，，要证明

_令 　　只要证明： 其中 .

令，则，所以在上是增函数，

则当时，，即 ，所以，

　则 .　 　　　　　　　　5分

[说明]也可用数学归纳法证明，为此，先证明即证： 其中.

21．(本题15分)

(Ⅰ)当A、D区域同时用红色鲜花时，其它区域不能用红色.

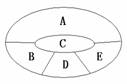(第21题)

因此，布置花圃的不同方法的种数为4´3´3 = 36种.…　　　　 ………………4分

　(穷举全部情况满分，部分情况酌情给分)

(Ⅱ)设M表示事件“恰有两个区域用红色鲜花”，

当区域A、D同色时，共有种；

当区域A、D不同色时，共有种；

因此，所有基本事件总数为：180+240=420种(是等可能的)……2分

又因为A、D为红色时，共有种；

B、E为红色时，共有种；

因此，事件M包含的基本事件有：36+36=72种．

所以，=．　　 ……………………………………………3分

(Ⅲ)随机变量的分布列为：

	0	1	2
P

　所以，=．……………………………………6分

20．(本题14分)由题意得.

(I)　　　　　　　 　　　　　　　　　　　　　　4分

(II)讨论：(1)当时，的零点；

　　　　　 (2)当时，的零点，不合题意； 　3分

(3)当时，

(4)当时，

综上所述，　　　　　　　 　　　　　　　　　　　　　　　　　　7分

(II)另解：在区间上存在零点，等价于在区间上有解，

也等价于直线与曲线有公共点，

作图可得　 .　 　　　　　　　　　　　　　　　　　　　　7分

或者：又等价于当时 ，求值域：.　　 7分

19． (本题14分)

(Ⅰ)，由OP⊥PQ，得

=0，

由，得cosa = ,

解得a < –2或a >2.　　　　　　　　　　　　　　　　　　　 7分

(Ⅱ)(向量坐标法)当a= –1时,

，

当，即时，取等号.　　　　　　　 7分

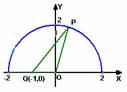
另证(余弦定理).如图， ，

设，则，

取等号时，，　　　　 7分