3．关于x的一元二次方程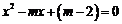的根的情况是 (　 )

　　　 A．有两个不相等的实数根　　 B．有两个相等的实数根　

　C．没有实数根　　　　　　　 D．无法确定　　 　

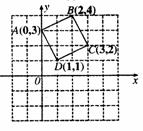
2．如图，在□ABCD中，在上，若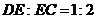，则BF：EF=(　　 )

A．1：2 　　B．1：3　

C．2：3　　 D．2：4　

1．右图是北京奥运会自行车比赛项目标志，图中两车轮所在圆

的位置关系是(　　 )

A．内含　　　　　　 B．相交 C．相切　　　　　 D．外离

21．(本题满分15分)

解： 函数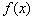的导函数为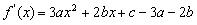　 　

(Ⅰ)由图可知　 函数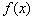的图像过点(0，3)，且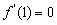

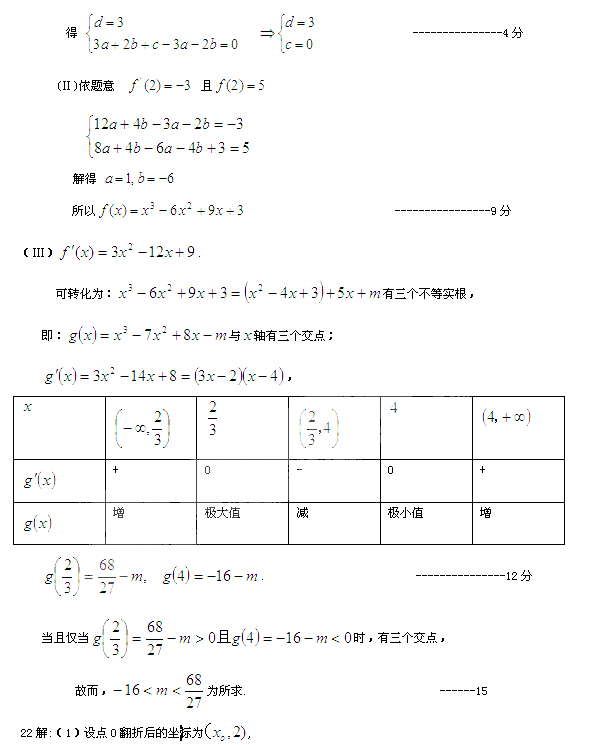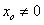当时，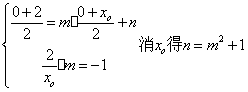

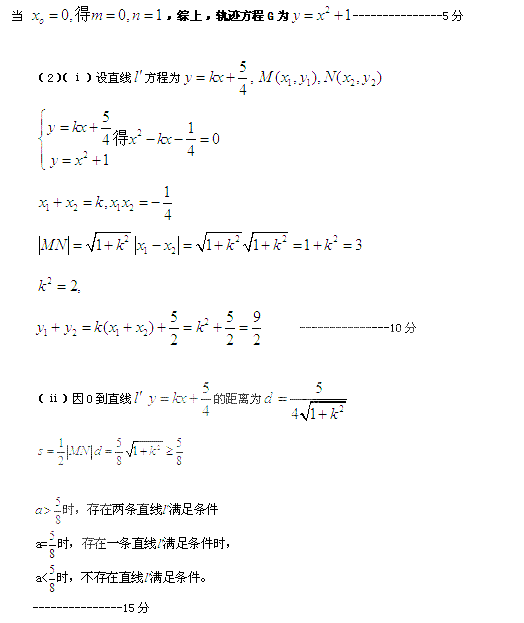
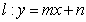
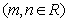22．(15分)如图，在直角坐标系中，坐标原点O(0，0),以动直线为轴翻折，使得每次翻折后点O都落在直线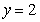上。(1)求以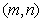为坐标的点的轨迹G的方程；

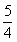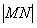(2)过点E(0，)作斜率为的直线交轨迹G于M,N两点；(ⅰ)当=3时，求M,N两点的纵坐标之和；(ⅱ)问是否存在直线，使OMN的面积等于某一给定的正常数，说明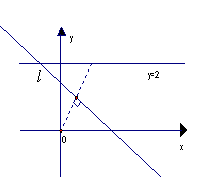你的理由。

慈溪中学2010届高三数学(文科)第二次月考答案

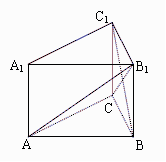
(3)作CF⊥AB，垂足为F，∵直三棱柱，平面A₁AB⊥平面ABC

　　 ∴CF⊥平面A₁AB　　　 ∴CF的长就是点C到平面A₁AB的距离

∵　　　　　　 (14分)

20．(14分)如图，在直三棱柱ABC-A₁B₁C₁中，∠ACB=90°，BC=CC₁=AC=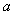

(1)求证：BC₁⊥平面AB₁C

(2)求二面角B-AB₁-C的大小

(3)求三棱锥A₁-AB₁C的体积

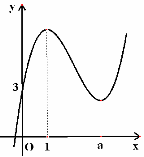21(15分)已知函数的图像如图 所示

(1)求的值；

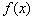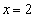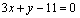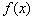(2)若函数在处的切线方程为，　 求函数的解析式；

(3)在(Ⅱ)的条件下，是否存在实数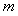，使得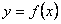的图像与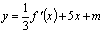的图像有且只有三个不同的交点？若存在，求出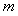的取值范围，若不存在，说明理由.

19．(14分)等差数列{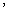 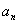}的各项为正整数，a₁=3，前n项和为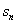，等比数列{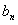}中，b₁=1，且b₂·S₂=16，b₃是a₁、a₂的等差中项

(1)求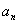与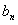； 　　　　　(2)求证：

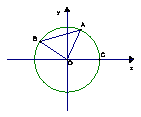
18. (14分)A、B是单位圆O上的动点，且A、B分别在第一、二象限，C是圆O与轴正半轴的交点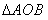， 为正三角形。记 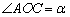(1)若A点的坐标为 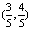，求 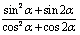的值　　 (2)求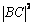的取值范围。

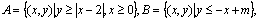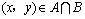17、设集合若，且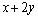的最大值为9，则 的值是　　　　 。

16. 已知函数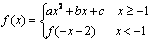，其图象在点(1,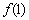)处的切线方程为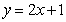,则它在点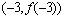处的切线方程为　　　　　 .