
4.(北京市宣武区2009-2010学年度第一学期期末质量检测)已知函数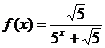 ,
,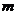 为正整数.
为正整数.
(Ⅰ)求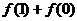 和
和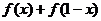 的值;
的值;
(Ⅱ)若数列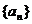 的通项公式为
的通项公式为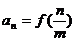 (
(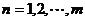 ),求数列
),求数列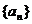 的前
的前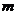 项和
项和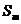 ;
;
(Ⅲ)设数列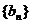 满足:
满足: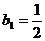 ,
,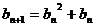 ,设
,设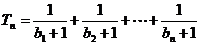 ,若(Ⅱ)中的
,若(Ⅱ)中的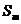 满足对任意不小于3的正整数n,
满足对任意不小于3的正整数n,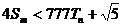 恒成立,试求m的最大值.
恒成立,试求m的最大值.
解:(Ⅰ)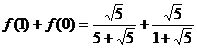 =1;
=1;
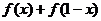 =
=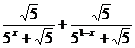 =
=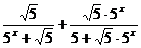 =1;………………………………4分
=1;………………………………4分
(Ⅱ)由(Ⅰ)得 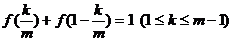 ,即
,即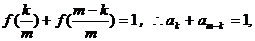
由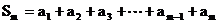 ,
……………①
,
……………①
得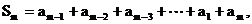 …………②
…………②
由①+②,
得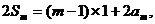 ∴
∴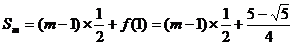 ,…10分
,…10分
(Ⅲ)
∵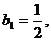
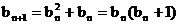 ,∴对任意的
,∴对任意的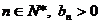 .
.
∴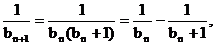 即
即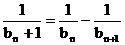 .
.
∴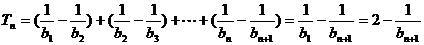 .
.
∵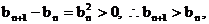 ∴数列
∴数列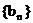 是单调递增数列.
是单调递增数列.
∴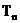 关于n递增.
当
关于n递增.
当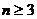 , 且
, 且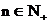 时,
时, 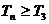 .
.
∵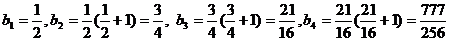
∴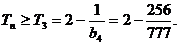 ∴
∴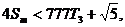 ∴
∴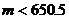 .而
.而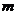 为正整数,
为正整数,
∴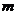 的最大值为650.
…………………………………………………………………………………14分
的最大值为650.
…………………………………………………………………………………14分
3.(石景山区2009-2010学年第一学期期末考试试卷)已知函数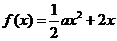 ,
,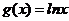 .
.
(Ⅰ)如果函数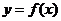 在
在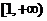 上是单调增函数,求
上是单调增函数,求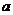 的取值范围;
的取值范围;
(Ⅱ)是否存在实数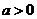 ,使得方程
,使得方程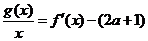 在区间
在区间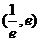 内有且只有两个不相等的实数根?若存在,请求出
内有且只有两个不相等的实数根?若存在,请求出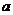 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
解:(Ⅰ)当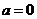 时,
时,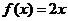 在
在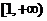 上是单调增函数,符合题意.………1分
上是单调增函数,符合题意.………1分
当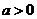 时,
时,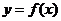 的对称轴方程为
的对称轴方程为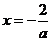 ,
,
由于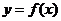 在
在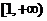 上是单调增函数,
上是单调增函数,
所以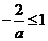 ,解得
,解得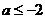 或
或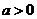 ,
,
所以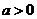 .
……………………3分
.
……………………3分
当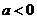 时,不符合题意.
时,不符合题意.
综上,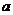 的取值范围是
的取值范围是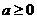 .
……………………4分
.
……………………4分
(Ⅱ)把方程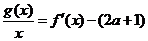 整理为
整理为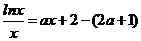 ,
,
即为方程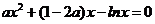 .
……………………5分
.
……………………5分
设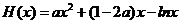
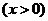 ,
,
原方程在区间(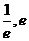 )内有且只有两个不相等的实数根, 即为函数
)内有且只有两个不相等的实数根, 即为函数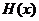 在区间(
在区间(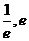 )内有且只有两个零点.
……………………6分
)内有且只有两个零点.
……………………6分
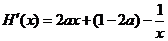
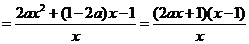 …………………7分
…………………7分
令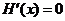 ,因为
,因为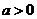 ,解得
,解得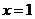 或
或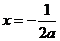 (舍) …………………8分
(舍) …………………8分
当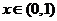 时,
时, 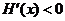 ,
, 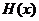 是减函数;
是减函数;
当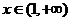 时,
时, 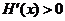 ,
,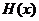 是增函数.
…………………10分
是增函数.
…………………10分
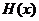 在(
在(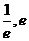 )内有且只有两个不相等的零点, 只需
)内有且只有两个不相等的零点, 只需
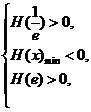 …………………13分
…………………13分
即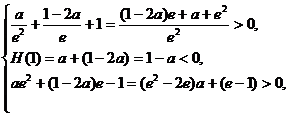 ∴
∴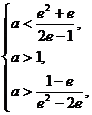
解得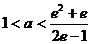 , 所以
, 所以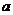 的取值范围是(
的取值范围是(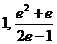 ) . …………………14分
) . …………………14分
注:若有其它解法,请酌情给分.
2.(海淀区高三年级第一学期期末练习)
给定项数为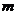
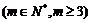 的数列
的数列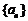 ,其中
,其中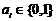
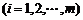 .
.
若存在一个正整数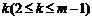 ,若数列
,若数列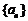 中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列
中存在连续的k项和该数列中另一个连续的k项恰好按次序对应相等,则称数列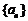 是“k阶可重复数列”,
是“k阶可重复数列”,
例如数列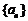
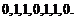
因为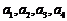 与
与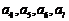 按次序对应相等,所以数列
按次序对应相等,所以数列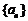 是“4阶可重复数列”.
是“4阶可重复数列”.
(Ⅰ)分别判断下列数列
①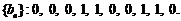 ②
②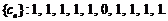
是否是“5阶可重复数列”?如果是,请写出重复的这5项;
(Ⅱ)若数为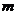 的数列
的数列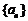 一定是 “3阶可重复数列”,则
一定是 “3阶可重复数列”,则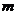 的最小值是多少?说明理由;
的最小值是多少?说明理由;
(III)假设数列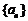 不是“5阶可重复数列”,若在其最后一项
不是“5阶可重复数列”,若在其最后一项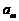 后再添加一项0或1,均可使新数列是“5阶可重复数列”,且
后再添加一项0或1,均可使新数列是“5阶可重复数列”,且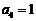 ,求数列
,求数列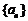 的最后一项
的最后一项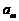 的值.
的值.
解:(Ⅰ)记数列①为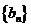 ,因为
,因为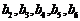 与
与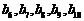 按次序对应相等,所以数列①是“5阶可重复数列”,重复的这五项为0,0,1,1,0;
按次序对应相等,所以数列①是“5阶可重复数列”,重复的这五项为0,0,1,1,0;
记数列②为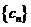 ,因为
,因为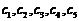 、
、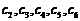 、
、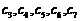 、
、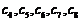 、
、 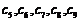 、
、 没有完全相同的,所以
没有完全相同的,所以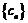 不是“5阶可重复数列”. ……………….3分
不是“5阶可重复数列”. ……………….3分
(Ⅱ)因为数列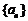 的每一项只可以是0或1,所以连续3项共有
的每一项只可以是0或1,所以连续3项共有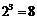 种不同的情形.若m=11,则数列
种不同的情形.若m=11,则数列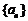 中有9组连续3项,则这其中至少有两组按次序对应相等,即项数为11的数列
中有9组连续3项,则这其中至少有两组按次序对应相等,即项数为11的数列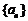 一定是“3阶可重复数列”;若m=10,数列0,0,1,0,1,1,1,0,0,0不是“3阶可重复数列”;则
一定是“3阶可重复数列”;若m=10,数列0,0,1,0,1,1,1,0,0,0不是“3阶可重复数列”;则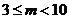 时,均存在不是“3阶可重复数列”的数列
时,均存在不是“3阶可重复数列”的数列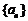 .所以,要使数列
.所以,要使数列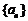 一定
一定
是“3阶可重复数列”,则m的最小值是11. ……………….8分
(III)由于数列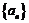 在其最后一项
在其最后一项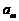 后再添加一项0或1,均可使新数列是“5阶可重复数列”,即在数列
后再添加一项0或1,均可使新数列是“5阶可重复数列”,即在数列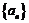 的末项
的末项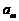 后再添加一项
后再添加一项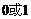 ,则存在
,则存在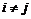 ,
,
使得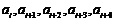 与
与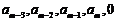 按次序对应相等,或
按次序对应相等,或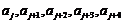 与
与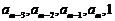 按次序对应相等,
按次序对应相等,
如果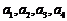 与
与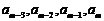 不能按次序对应相等,那么必有
不能按次序对应相等,那么必有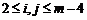 ,
,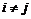 ,使得
,使得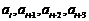 、
、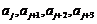 与
与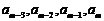 按次序对应相等.
按次序对应相等.
此时考虑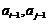 和
和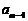 ,其中必有两个相同,这就导致数列
,其中必有两个相同,这就导致数列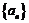 中有两个连续的五项恰按次序对应相等,从而数列
中有两个连续的五项恰按次序对应相等,从而数列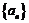 是“5阶可重复数列”,这和题设中数列
是“5阶可重复数列”,这和题设中数列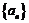 不是“5阶可重复数列”矛盾!所以
不是“5阶可重复数列”矛盾!所以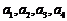 与
与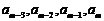 按次序对应相等,从而
按次序对应相等,从而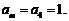
……………….14分
说明:其它正确解法按相应步骤给分.
1.(东城区2009-2010学年度第一学期期末教学目标检测)设数列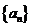 的前
的前 项和为
项和为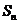 .已知
.已知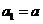
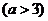 ,
,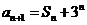 ,
,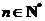 .
.
(Ⅰ)设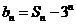 ,求数列
,求数列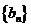 的通项公式;
的通项公式;
(Ⅱ)若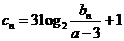
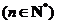 ,证明对任意的
,证明对任意的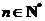 ,
,
不等式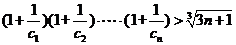 恒成立.
恒成立.
解:(Ⅰ)依题意,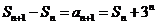 ,即
,即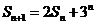 ,
,
由此得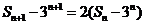 .
.
因此,所求通项公式为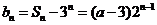 ,
,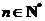 .……………………5分
.……………………5分
(Ⅱ)证明:由已知 ,
,
则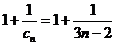 ,所以
,所以
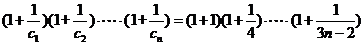 .……………………7分
.……………………7分
下面用数学归纳法证明不等式
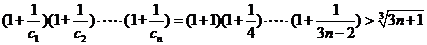 成立.
成立.
①当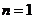 时,左边=
时,左边=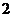 ,右边=
,右边=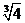 ,因为
,因为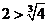 ,所以不等式成立. …………………8分
,所以不等式成立. …………………8分
②假设当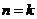 时不等式成立,即
时不等式成立,即
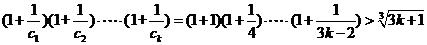 成立.
成立.
则当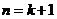 时,左边
时,左边
=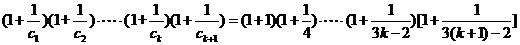
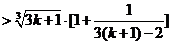
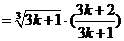
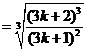 .……………………………………………………………………………11分
.……………………………………………………………………………11分
要证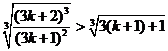 成立,
成立,
只需证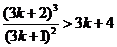 成立,
成立,
由于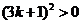 ,
,
只需证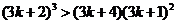 成立,
成立,
只需证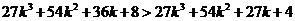 成立,
成立,
只需证 成立,
成立,
由于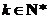 ,所以
,所以 成立.
成立.
即
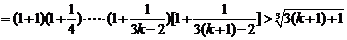 成立.
成立.
所以当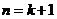 时,不等式也成立.
时,不等式也成立.
由①,②可得不等式恒成立. ………………………………………………………………14分
35.我国是一个多山的国家,是世界上泥石流灾情最严重的国家之一。分析下列材料,回答问题。(10分)
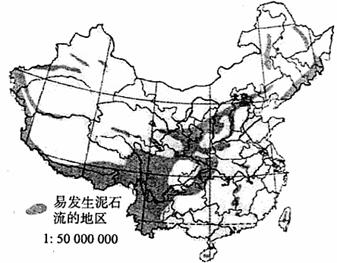
材料一 中国泥石流分布图。
材料二 2008年9月22-27日,四川省先后有12市38个县(市)遭受暴雨袭击,其中多个县(市)出现大暴雨;峨眉山市日最大降水量达159.8毫米;北川县连续5天出现暴雨。地震灾区泥石流频发,造成严重人员伤亡和财产损失,部分地方道路中断,对灾区的恢复重建十分不利。
(1)据材料一说出我国泥石流的主要集中分布地区。(2分)
(2)据材料二并结合所学知识,简要分析四川灾区该次泥石流形成的主要原因。(4分)
(3)为减轻川滇山地的泥石流对人类的危害,列举应采取的应对措施。(4分)
34.2006年夏季,重庆市遭遇百年不遇的特大干旱。为挽回旱灾的部分经济损失,重庆市政府组织农民工赴新疆摘棉花。事实上,以前就有大量重庆民工到新疆摘棉花。读图回答问题。(13分)
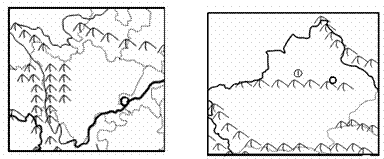
(1)试分析上图中两区域差异最大的气候特征。(2分)
(2)制约新疆棉花生产规模进一步扩大的最不利自然条件是什么?其针对这一不利条件在生产中应采取什么措施?(2分)
(3)试分析重庆农民工赴新疆摘棉花的社会经济原因?(3分)
(4)重庆某乡镇的小明先去成都与表哥汇合,再去南疆摘棉花,如何走最近?请你帮他选择经过的主要铁路线。(4分)
(5)右图中①山脉是我国西部两大盆地的分界。山脉北侧的盆地中多半固定沙丘而南侧多为流动沙丘,试根据所学知识分析这种差异形成的自然原因。(2分)
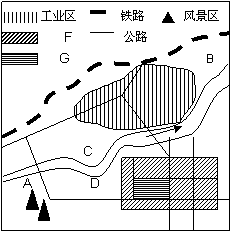
33.右图为某城市示意图,读图回答下列问题。(11分)
(1)若图中工业区布局合理,则该市主导风向是 。(2分)
(2)除考虑风向外,从图中分析该市工业布局的合理性有哪些?(4分)
(3)F、G所示两地中,表示商业中心的是 地。(2分)
(4)A、B、C、D四地中,最适宜建高级住宅区的是 地,原因有什么?(3分)
32.读图回答问题。(12分)

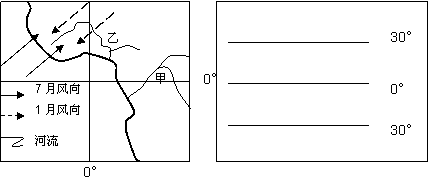
(1)说出图中夏季风的成因以及对此区域气候的影响?(4分)
 (2)在右侧方框内画出1月赤道附近的气压带、风带分布示意图(用 表示低压带,箭头表示风向)(2分)
(2)在右侧方框内画出1月赤道附近的气压带、风带分布示意图(用 表示低压带,箭头表示风向)(2分)
(3)甲乙两河流从源头到入海,流量经过明显的多→少→多变化的是 ,并简要分析原因。(3分)
(4)甲河流域面临的主要生态环境问题有哪些?(3分)
31.读我国西南地区两城市(M、N)有关气象资料,回答问题。
(9分)
表一:M和N两地气温年、日较差比较
|
|
年较差 (℃) |
日较差(℃) |
||||
|
年平均 |
1月 |
4月 |
7月 |
10月 |
||
|
M |
12.1 |
11.1 |
13.9 |
14.8 |
7.2 |
8.8 |
|
N |
19.1 |
8.0 |
6.9 |
9.3 |
8.0 |
7.5 |
表二:M和N两地的降水量及占全年比重、降水日数比较
|
|
11-4月 |
5-10月 |
||||
|
|
降水量(mm) |
全年比重(%) |
降水日数(天) |
降水量 (mm) |
全年比重(%) |
降水日数(天) |
|
M |
116.3 |
11.2 |
31.0 |
918.1 |
88.8 |
103.6 |
|
N |
278.5 |
24.7 |
80.9 |
849.8 |
75.3 |
98.0 |
(1)比较M和N气温年较差、日较差的不同点。(2分)
(2)1月M和N的气温日较差相差 ℃,达到全年差异最大值。根据上述材料分析1月M气温日较差大于N的原因。(5分)
(3)分析M、N两地5-10月降水多于11-4月的原因。(2分)
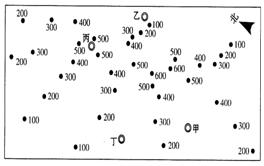 读华北地区某地实测的海拔高度数据分布,回答29-30题。
读华北地区某地实测的海拔高度数据分布,回答29-30题。
29.测量图中各地海拔高度所用最精准、便
捷的技术是
A.遥感 B.全球定位系统
C.数字地球 D.地理信息系统
30.对图示区域地理特征的描述,正确的是
A.海拔 甲>丙 B.坡度 甲>乙
C.气温 丙>丁 D.降水 乙>丁
普通高中阶段性评估练习题
高三地理 2010.02
第Ⅱ卷 (综合题55分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com