20、(12分)

解：(1)由题知：BC=AD=GD　　 又因为四边形ABCD为梯形，所以BC∥GD

所以BCDG为平行四边形，从而BG∥CD

　　 因为BG面PCD，CD面PCD

所以BG∥面PCD　　　　　 (4分)

　 (2)因为PA面ABCD，所以DAPA 又知DAAB，ABPA=A

从而DA面PAB。又因为DA面DAMN　

　　　 所以面DAMN面PAB。　　 (8分)

　 (3)由于CD∥BG，所以CD和BG与面DAMN的成的角相等。

　　　 因为AB=AP且M为PB中点，所以BMAM

　　 又因为面DAMN面PAB。且面DAMN面PAB=AM　　 所以BM面DAMN，　 连结MG。

　　 则BGM为BG与面DAMN所成的角。

　　　 设AB=2，则PB=2，BM=，BG==

　　　 在BMG中，

所以BG即CD与面DAMN所成的角的大小为　　 (12分)

19、(12分)

　 解：(1)二项式(的展开式的前三项的系数为

　　 1，，由题意得

　 1+　 解得n=8　　　　　 (6分)

(2) 已知=

令x=0, 得

18、(12分)

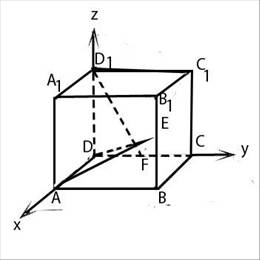
解：　 如图，以DA、DC、DD₁分别出

作为x,y,z轴，建立空间坐标系。

则A(2，0，0)　 C(0，2，0)

D₁(0，0，2)　 E (2，2，1)F(0，1，0)　 B(2，2，0)。则

17、(10分)

解：(1)可从7人中任选3人，即=35种不同的选法。　 (2分)

　 (2)至少有一名女生当选的不同选法有 　　　　　　　　

　　 种　 或种　　　　 (6分)

　　　 (3)代表中男、女生都要有的不同选取法有

　　 种　　　　　 (10分)

13、　　　 14、 58个　 .　 _­­15、.　 16、 　② ④　

22、(分12)如图，在四面体ABCD中，ABC与DBC都是边长为4的正三角形。

(1)求证：BCAD；

(2)若D点到面ABC的距离不小于3， 求二面角A-BC-D的平面角的取值范围。　

个旧一中2008-----2009学年上学期高二年级期中考试

　　　　　　　　　　　 　　　数学试题　

　　　　　　 命题人：罗荣章　　　　　　　　　　　　　

21、(12分)某校高二年级有6个班，现有四个“三好”学生名额，要分配给这六个班。

⑴ 把四个名额全部分给一个班，有多少种不同分法？

⑵ 把四个名额全部分给其中的两个班，每班至少一个名额，有多种不同的分法？

⑶ 把这四个名额全部分完，有多少种不同的分法？

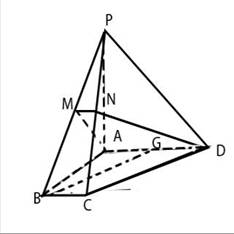
20、(12分)如图：在四棱锥P-ABCD中，底面ABCD为直角梯形AD∥BC，，PA底面ABCD，且PA=AD=AB=2BC，M、N、G分别是PB、PC、AD中点。

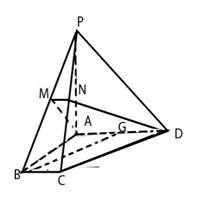⑴ 证明：BG∥面PCD。

⑵ 证明:面DAMN面PAB。

⑶ 求CD与面DAMN所成的角的大小。

19、(12分)已知二项式(的展开式的前三项的系数成等差数列。

(1) 求的值。

(2)已知=。求及的值。

18、(12分)(如图)在正方体ABCD-A₁B₁C₁D₁中，E、F分别是BB₁、CD的中点，边长为2。

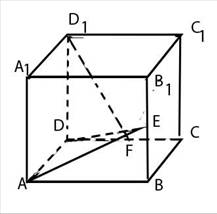
(1)求证：D₁F面ADE。

(2)求点B到面ADE的距离。

(3)求异面直线D₁F与AC所成的角的大小。