
(湛江二中2010届高三第二次月考语文试卷)
1.下列词语中加点字的读音完全相同的一组是( )(3分) 
A.狂飙 镖局 骠勇善战
分道扬镳 
B.胆怯 惬意 提纲挈领 度长絜大
C.臭氧 铜臭 臭味相投
遗臭万年
D.沏茶 蹊跷 栖身之所
休戚相关
20.解:(Ⅰ)因为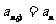 ,所以
,所以 ,解得
,解得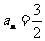 或
或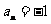 (舍去).
(舍去).
由 的任意性知,
的任意性知, .
………………… 3分
.
………………… 3分
(Ⅱ)反证法:
假设 ,则
,则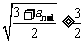 ,得
,得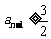 ,
,
依此类推, ,…,
,…,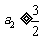 ,
,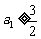 ,与
,与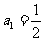 矛盾.
矛盾.
所以 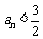 .
………………… 8分
.
………………… 8分
(Ⅲ)由已知,当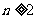 时,
时,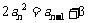 ,
,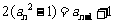 ,
,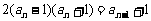 ,
,
所以 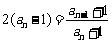 .
.
同理 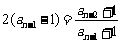 ,…,
,…,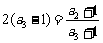 ,
,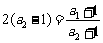 .
.
将上述 个式子相乘,得
个式子相乘,得
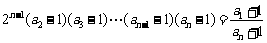 ,
,
即 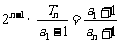 ,
,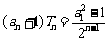 .
.
所以 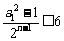 对任意
对任意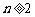 恒成立.
恒成立.
又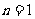 时,
时,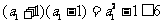 ,
,
故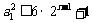 对任意
对任意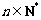 恒成立.
恒成立.
因为数列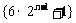 单调递增,所以
单调递增,所以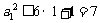 ,
,
即 的取值范围是
的取值范围是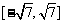 .
………………… 14分
.
………………… 14分
19.解:(Ⅰ)由已知可得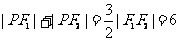
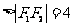 ,
,
故曲线 是以
是以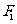 ,
,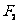 为焦点,长轴长为
为焦点,长轴长为 的椭圆,其方程为
的椭圆,其方程为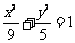 . ………………… 5分
. ………………… 5分
(Ⅱ)方法一:设
 ,由条件可知
,由条件可知 为
为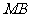 的中点,
的中点,
则有  ………………… 9分
………………… 9分
将(3)、(4)代入(2)得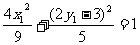 ,整理为
,整理为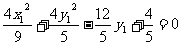 .
.
将(1)代入上式得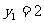 ,再代入椭圆方程解得
,再代入椭圆方程解得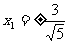 ,
,
故所求的直线方程为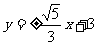 .
………………… 13分
.
………………… 13分
方法二:依题意,直线 的斜率存在,设其方程为
的斜率存在,设其方程为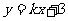 .
.
由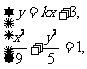 得
得 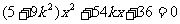 . 令
. 令 ,解得
,解得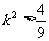 .
.
设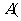
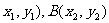 , 则
, 则 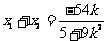 , ①
, ① 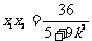 . ②
………… 8分
. ②
………… 8分
因为 ,所以
,所以 为
为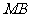 的中点,从而
的中点,从而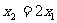 .
.
将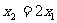 代入 ①、② ,得
代入 ①、② ,得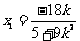 ,
,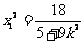 ,
,
消去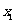 得
得 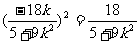 ,
………………… 11分
,
………………… 11分
解得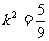 ,
,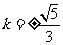 .
.
所以直线 的方程为
的方程为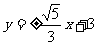 .
………………… 13分
.
………………… 13分
18.解:(Ⅰ)若 ,
, ,则点
,则点 的个数共有
的个数共有 个,列举如下:
个,列举如下:
 ,
,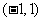 ,
,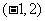 ,
,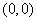 ,
,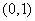 ,
,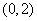 ,
,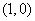 ,
,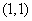 ,
,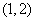 ,
,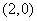 ,
,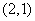 ,
,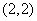 .
.
当点 的坐标为
的坐标为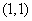 ,
,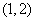 ,
,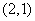 ,
,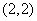 时,点
时,点 位于第一象限,
位于第一象限,
 故点
故点 位于第一象限的概率为
位于第一象限的概率为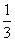 . …………………
5分
. …………………
5分
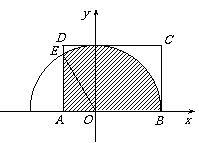
(Ⅱ)这是一个几何概率模型.
如图,若 ,
, ,则区域
,则区域 的面积是
的面积是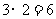 .
.
满足 的点
的点 构成的区域为
构成的区域为
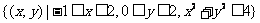 ,即图中的阴影部分.
………………… 9分
,即图中的阴影部分.
………………… 9分
易知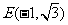 ,
,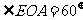 ,
,
所以扇形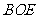 的面积是
的面积是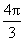 ,
,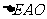 的面积是
的面积是 ,
,
故 的概率为
的概率为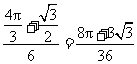 .
………………… 13分
.
………………… 13分
17.解:(Ⅰ)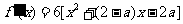
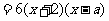 .
………………… 3分
.
………………… 3分
当 时,
时,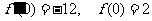 ,
,
所以切线方程为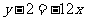 ,即
,即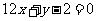 .
………………… 6分
.
………………… 6分
(Ⅱ)令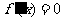 ,解得:
,解得: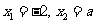 .
.
① 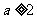 ,则当
,则当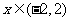 时,
时,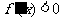 ,函数
,函数 在
在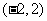 上单调递减,
上单调递减,
所以,当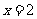 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为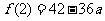 . ………………… 8分
. ………………… 8分
② 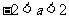 ,则当
,则当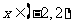 时,
时,
当 变化时,
变化时,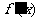 ,
, 的变化情况如下表:
的变化情况如下表:
 |
 |
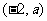 |
 |
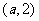 |
 |
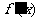 |
|
 |
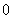 |
 |
|
 |
 |
 |
极小值 |
 |
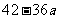 |
所以,当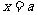 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为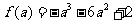 .………………… 11分
.………………… 11分
③  ,则当
,则当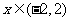 时,
时,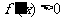 ,函数
,函数 在
在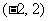 上单调递增,
上单调递增,
所以,当 时,函数
时,函数 取得最小值,最小值为
取得最小值,最小值为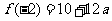 . ………………… 13分
. ………………… 13分
综上,当 时,
时, 的最小值为
的最小值为 ;当
;当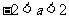 时,
时, 的最小值为
的最小值为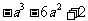 ;当
;当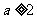 时,
时, 的最小值为
的最小值为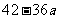 .
………………… 14分
.
………………… 14分
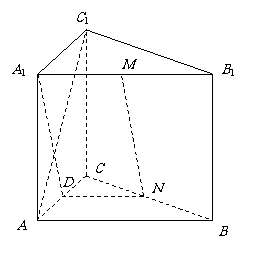
16.证明:(Ⅰ)方法一:因为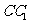
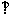 平面
平面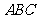 ,
,
所以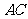 是
是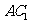 在平面
在平面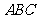 内的射影.…… 4分
内的射影.…… 4分
由条件可知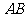
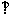
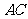 ,
,
所以 .
………………… 6分
.
………………… 6分
方法二:
因为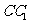
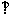 平面
平面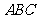 ,
,
又 平面
平面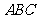 ,
,
所以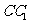
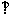
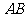 .
.
由条件 ,即
,即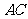
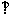
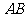 ,
,
且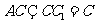 ,
,
所以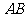
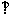 平面
平面 .
………………… 4分
.
………………… 4分
又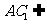 平面
平面 ,
,
所以 .
………………… 6分
.
………………… 6分
(Ⅱ)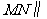 平面
平面 ,证明如下:
………………… 8分
,证明如下:
………………… 8分
设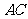 的中点为
的中点为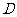 ,
,
连接 ,
,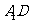 .
.
因为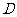 ,
, 分别是
分别是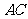 ,
, 的中点,
的中点,
所以
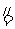
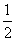
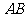 .
.
又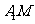 =
=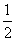
 ,
,
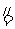
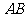 ,
,
所以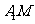
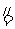
 .
.
所以四边形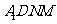 是平行四边形.
是平行四边形.
所以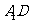
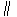
 .
………………… 11分
.
………………… 11分
因为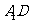
 平面
平面 ,
,
 平面
平面 ,
,
所以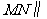 平面
平面 .
………………… 13分
.
………………… 13分
15.解:(Ⅰ)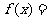
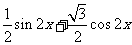 ………………… 3分
………………… 3分
 2
………………… 5分
2
………………… 5分
所以
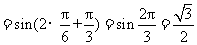 .
………………… 7分
.
………………… 7分
(Ⅱ)当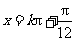 (
(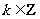 )时,
)时, 的最大值是
的最大值是 .
………………… 9分
.
………………… 9分
由 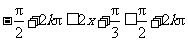 ,
,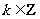 ,
,
得 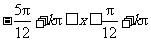 ,
,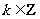 .
.
所以 的单调递增区间为
的单调递增区间为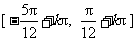 ,
,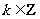 .
………………… 13分
.
………………… 13分
9.甲 10.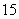 11.
11.
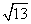 12.
12.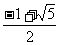 13.
13.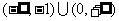 14.
14.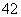
1.A 2.C 3.C 4.B 5.D 6.B 7.D 8.A
20.(本小题满分14分)
数列 满足
满足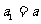 ,
,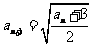 ,
,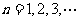 .
.
(Ⅰ)若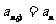 ,求
,求 的值;
的值;
(Ⅱ)当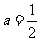 时,证明:
时,证明: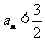 ;
;
(Ⅲ)设数列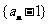 的前
的前 项之积为
项之积为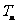 .若对任意正整数
.若对任意正整数 ,总有
,总有 成立,求
成立,求 的取值范围.
的取值范围.
数学 (文科)评分参考
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com