19．(本题满分14分)

已知数列时，总成等差数列。

　 (1)求数列的通项公式；

　 (2)若数列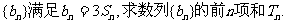

18．(本题满分14分)

设函数

　 (I)求函数的最小正周期及函数的单调递增区间；

　 (II)若，是否存在实数m，使函数？若存在，请求出m的取值；若不存在，请说明理由。

16．已知钝角三角形ABC的最大边长为4，其余两边长分别为x，y，那么以为坐标的点所表示的平面区域的面积是　　　　　 。

　 17．如图，平面，AD=4，BC=8，AB=6，在平面上的动点P，记PD与

平面所成角为，PC与平面，若，

则△PAB的面积的最大值是　　　　 。

15．设向量=　　　　 。

14．根据市场调查，某商品在最近10天内的价格(单位：

元/件)与时间t满足关系

销售量(单位：万件)与时间t满足关系，则这种商品的日销售额的最大值为　　　　 (万元)。

13．在△ABC中，若

则AB=　　　 。

　 11．若等比数列=　　　　　 。

12．如果一个几何体的三视图如图所示(单位长度：cm)，

则此几何体的体积是　　　 　　。

10．设圆，使(O为坐标原点)，则的取值范围是　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．[]　　　　　　　 B．[0，1]　　　　　　　　 C．　　　　　　　　 D．

9．设双曲线的半焦距为c，直线两点，若原点O到直线l的距离为，则双曲线的离心率为　　　　　　　　　　　　　　　　　　　 (　　 )

　　　 A．　　　　　 B．2　　　　　　　　　　　　 C．　　　　 D．

8．两人掷一枚硬币，掷出正面者胜，但这枚硬币不均匀，以致出现正面的概率P₁与出现反面的概率P₂不相等，已知出现正面与出现反面是对立事件，设两人各掷一次成平局的概率为P，则P与0.5的大小关系是　　　　　　　　 (　 　)

　　　 A．P<0.5　　　　　　　　 B．P=0.5　　　　　　　　　 C．P>0.5　　　　　　　　 D．不确定