10．复数与几何。

例13　 如图15-2所示，在四边形ABCD内存在一点P，使得ΔPAB，ΔPCD都是以P为直角顶点的等腰直角三角形。求证：必存在另一点Q，使得ΔQBC，ΔQDA也都是以Q为直角顶点的等腰直角三角形。

例14　 平面上给定ΔA₁A₂A₃及点p₀，定义A_s=A_s-3,s≥4，构造点列p₀,p₁,p₂,…,使得p_k+1为绕中心A_k+1顺时针旋转120⁰时p_k所到达的位置，k=0,1,2,…,若p₁₉₈₆=p₀.证明：ΔA₁A₂A₃为等边三角形。

9.单位根的应用。

例12　 证明：自⊙O上任意一点p到正多边形A₁A₂…A_n各个顶点的距离的平方和为定值。

8．复数与多项式。

例11　 已知f(z)=c₀zⁿ+c₁z^n-1+…+c_n-1z+c_n是n次复系数多项式(c₀≠0).

求证：一定存在一个复数z₀,|z₀|≤1，并且|f(z₀)|≥|c₀|+|c_n|.

7．复数与三角。

例9　 已知cosα+cosβ+cosγ=sinα+sinβ+sinγ=0，求证：cos2α+cos2β+cos2γ=0。

例10　 求和：S=cos20⁰+2cos40⁰+…+18cos18×20⁰.

6．复数与轨迹。

例8　 ΔABC的顶点A表示的复数为3i，底边BC在实轴上滑动，且|BC|=2，求ΔABC的外心轨迹。

5．复数乘法的几何意义。

例6　 以定长线段BC为一边任作ΔABC，分别以AB，AC为腰，B，C为直角顶点向外作等腰直角ΔABM、等腰直角ΔACN。求证：MN的中点为定点。

例7　 设A，B，C，D为平面上任意四点，求证：AB•AD+BC•AD≥AC•BD。

4．二项式定理的应用。

例5　 计算：(1)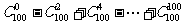；(2)

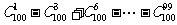
3．三角形式的应用。

例4　 设n≤2000,n∈N，且存在θ满足(sinθ+icosθ)ⁿ=sinnθ+icosnθ，那么这样的n有多少个？

2.复数相等。

例3　 设λ∈R，若二次方程(1-i)x²+(λ+i)x+1+λi=0有两个虚根，求λ满足的充要条件。

1．模的应用。

例1　 求证：当n∈N₊时，方程(z+1)²ⁿ+(z-1)²ⁿ=0只有纯虚根。

例2　 设f(z)=z²+az+b,a,b为复数，对一切|z|=1，有|f(z)|=1，求a,b的值。