
5.在△ABC中,“a>b”是“sinA>sinB”的__________条件.
4.在△ABC中,3sinA+4cosB=6, 3cosA+4sinB=1,则 =__________.
=__________.
3.在△ABC中,a=4, b+c=5, tanC+tanB+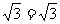 tanCtanB,则△ABC的面积为__________.
tanCtanB,则△ABC的面积为__________.
2.在△ABC中,若AB=1,BC=2,则 的取值范围是__________.
的取值范围是__________.
1.在△ABC中,边AB为最长边,且sinAsinB=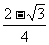 ,则cosAcosB的最大值为__________.
,则cosAcosB的最大值为__________.
4.三角换元。
例5 设a, b, c∈R+,且abc+a+c=b,试求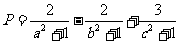 的最大值。
的最大值。
例6 在△ABC中,若a+b+c=1,求证: a2+b2+c2+4abc<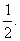
3.一个常用的代换:在△ABC中,记点A,B,C到内切圆的切线长分别为x, y, z,则a=y+z, b=z+x, c=x+y.
例4 在△ABC中,求证:a2(b+c-a)+b2(c+a-b)+c2(a+b-c) ≤3abc.
2.正弦定理的应用。
例2 △ABC内有一点P,使得 BPC-
BPC- BAC=
BAC= CPA-
CPA- CBA=
CBA= APB-
APB- ACB。
ACB。
求证:AP·BC=BP·CA=CP·AB。
例3 △ABC的各边分别与两圆⊙O1,⊙O2相切,直线GF与DE交于P,求证:PA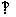 BC。
BC。
1.面积法。
例1 (共线关系的张角公式)如图所示,从O点发出的三条射线满足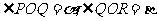 ,另外OP,OQ,OR的长分别为u, w, v,这里α,β,α+β∈(0,
,另外OP,OQ,OR的长分别为u, w, v,这里α,β,α+β∈(0,  ),则P,Q,R的共线的充要条件是
),则P,Q,R的共线的充要条件是
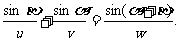
2.余弦定理:a2=b2+c2-2bccosA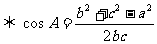 ,下面用余弦定理证明几个常用的结论。
,下面用余弦定理证明几个常用的结论。
(1)斯特瓦特定理:在△ABC中,D是BC边上任意一点,BD=p,DC=q,则AD2=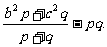 (1)
(1)
[证明] 因为c2=AB2=AD2+BD2-2AD·BDcos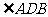 ,
,
所以c2=AD2+p2-2AD·pcos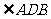 ①
①
同理b2=AD2+q2-2AD·qcos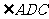 ,
②
,
②
因为 ADB+
ADB+ ADC=
ADC= ,
,
所以cos ADB+cos
ADB+cos ADC=0,
ADC=0,
所以q×①+p×②得
qc2+pb2=(p+q)AD2+pq(p+q),即AD2=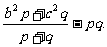
注:在(1)式中,若p=q,则为中线长公式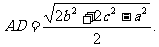
(2)海伦公式:因为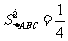 b2c2sin2A=
b2c2sin2A=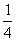 b2c2
(1-cos2A)=
b2c2
(1-cos2A)= 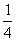 b2c2
b2c2
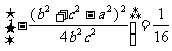 [(b+c)
[(b+c)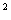 -a2][a2-(b-c)
2]=p(p-a)(p-b)(p-c).
-a2][a2-(b-c)
2]=p(p-a)(p-b)(p-c).
这里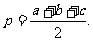
所以S△ABC=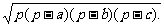
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com