
2.一个从地面竖直上抛的物体,它两次经过一个较低的点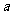 的时间间隔是
的时间间隔是 ,两次经过一个较高点
,两次经过一个较高点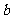 的时间间隔是
的时间间隔是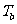 ,则
,则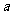 、
、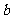 之间的距离为
之间的距离为
A.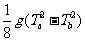 B.
B.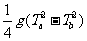
C.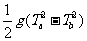 D.
D.
1.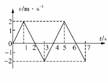 某物体的运动规律如图所示,下列说法正确的是
某物体的运动规律如图所示,下列说法正确的是
A.物体在第1s末运动方向发生变化
B.第2s内、第3s内的速度方向是相同的
C.物体在第2s内返回出发点,向反方向运动
D.在这7s内物体的位置始终不会为负值
23.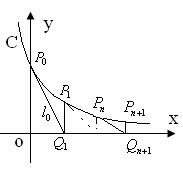 (本小题14分)如图,过曲线C:
(本小题14分)如图,过曲线C: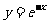 上一点
上一点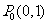 做曲线C的切线
做曲线C的切线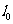 交x轴于
交x轴于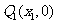 点,又过
点,又过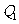 做x轴的垂线交曲线C于
做x轴的垂线交曲线C于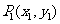 点,然后再过
点,然后再过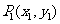 做曲线C的切线
做曲线C的切线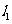 交x轴于
交x轴于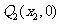 ,又过
,又过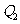 做x轴的垂线交曲线C于
做x轴的垂线交曲线C于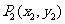 ,
, ,以此类推,过点
,以此类推,过点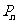 的切线
的切线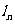 与x轴相交于点
与x轴相交于点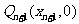 ,再过点
,再过点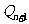 做x轴的垂线交曲线C于点
做x轴的垂线交曲线C于点 (n=1,2,3,…).
(n=1,2,3,…).
(1)求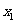 、
、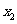 及数列
及数列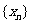 的通项公式;
的通项公式;
(2)设曲线C与切线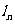 及垂线
及垂线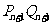 所围成的图形面积为
所围成的图形面积为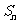 ,求
,求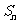 的表达式;
的表达式;
(3)若数列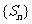 的前n项之和为
的前n项之和为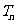 ,求证:
,求证: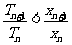
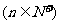 .
.
西工大附中高2010届第一次摸拟考试
22、(本小题13分)已知椭圆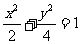 两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足
两焦点分别为F1、F2,P是椭圆在第一象限弧上一点,并满足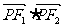 =1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
=1,过P作倾斜角互补的两条直线PA、PB分别交椭圆于A、B两点.
(1)求P点坐标; (2)求直线AB的斜率;
(3)求△PAB面积的最大值.
21. (本小题12分)已知函数
(本小题12分)已知函数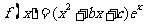 在点
在点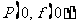 处的切线方程为
处的切线方程为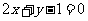 .
.
(1)求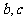 的值;(2)求函数
的值;(2)求函数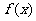 的单调区间;
的单调区间;
(3)若方程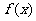 =m恰有两个不等的实根,求m的取值范围.
=m恰有两个不等的实根,求m的取值范围.
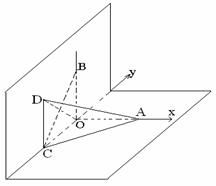
20.(本小题12分)在平面直角坐标系xoy中,已知四点A(2,0),B(-2,0),C(0,-2),D(-2,-2),把坐标系平面沿y轴折为直二面角.
(1)求证:BC⊥AD;
(2)求二面角C-AD-O的大小;
(3)求三棱锥C-AOD的体积.

19.(本小题12分)某部门为每位“志愿者”进行上岗培训,每人可以选择参加一项培训、参加两项培训或不参加培训,已知参加过礼仪培训的有75%,参加过实用语言培训的有60%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.
(1)任选1名“志愿者”,求该人参加过培训的概率;
(2)任选3名“志愿者”,记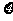 为3人中参加过培训的人数,求
为3人中参加过培训的人数,求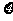 的分布列和期望.
的分布列和期望.
18.(本小题12分)已知向量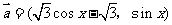 ,
,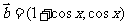 ,设
,设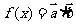 .
.
(1).求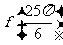 的值;
的值;
(2).当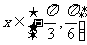 时,求函数
时,求函数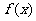 的值域。
的值域。
(二)选做题(15-17题,考生只能从中选做一题)
15.(选修4-4坐标系与参数方程)曲线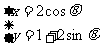 与
与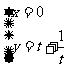 交点的个数为:
;
交点的个数为:
;
16.(选修4-5 不等式选讲)不等式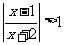 的解集是:
;
的解集是:
;
17.(选修4-1 几何证明选讲)已知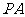 是圆
是圆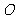 的切线,切点为
的切线,切点为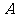 ,
,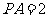 .
. 是圆
是圆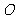 的直径,
的直径,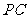 与圆
与圆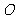 交于点
交于点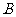 ,
,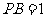 ,则圆
,则圆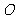 的半径
的半径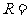 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com