
3.已知函数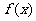 是偶函数,而且在
是偶函数,而且在 上是减函数,判断
上是减函数,判断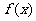 在
在 上是增函数还是减函数,并证明你的判断.
上是增函数还是减函数,并证明你的判断.
2.解:由矩形的宽为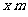 ,得矩形的长为
,得矩形的长为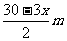 ,设矩形的面积为
,设矩形的面积为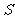 ,
,
则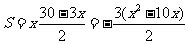 ,
,
当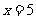 时,
时,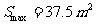 ,
,
即宽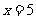
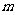 才能使建造的每间熊猫居室面积最大,
才能使建造的每间熊猫居室面积最大,
且每间熊猫居室的最大面积是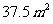 .
.
2.如图所示,动物园要建造一面靠墙的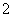 间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是
间面积相同的矩形熊猫居室,如果可供建造围墙的材料总长是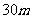 ,那么宽
,那么宽 (单位:
(单位: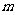 )为多少才能使建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?
)为多少才能使建造的每间熊猫居室面积最大?每间熊猫居室的最大面积是多少?

1.解:(1)二次函数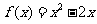 的对称轴为
的对称轴为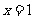 ,
,
则函数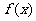 的单调区间为
的单调区间为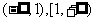 ,
,
且函数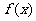 在
在 上为减函数,在
上为减函数,在 上为增函数,
上为增函数,
函数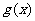 的单调区间为
的单调区间为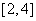 ,
,
且函数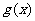 在
在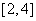 上为增函数;
上为增函数;
(2)当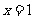 时,
时,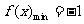 ,
,
因为函数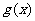 在
在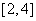 上为增函数,
上为增函数,
所以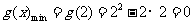 .
.
1.已知函数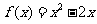 ,
,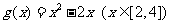 .
.
(1)求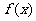 ,
,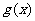 的单调区间; (2)求
的单调区间; (2)求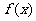 ,
,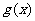 的最小值.
的最小值.
6.解:当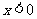 时,
时,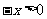 ,而当
,而当 时,
时,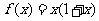 ,
,
即 ,而由已知函数是奇函数,得
,而由已知函数是奇函数,得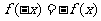 ,
,
得 ,即
,即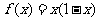 ,
,
所以函数的解析式为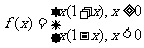 .
.
B组
6.已知函数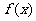 是定义在
是定义在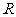 上的奇函数,当
上的奇函数,当 时,
时,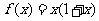 .画出函数
.画出函数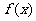
的图象,并求出函数的解析式.
5.解:对于函数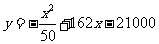 ,
,
当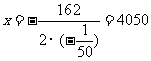 时,
时,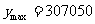 (元),
(元),
即每辆车的月租金为 元时,租赁公司最大月收益为
元时,租赁公司最大月收益为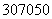 元.
元.
5.某汽车租赁公司的月收益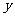 元与每辆车的月租金
元与每辆车的月租金 元间的关系为
元间的关系为
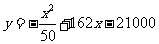 ,那么,每辆车的月租金多少元时,租赁公司的月收益最大?最大月收益是多少?
,那么,每辆车的月租金多少元时,租赁公司的月收益最大?最大月收益是多少?
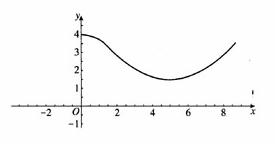
4.解:自服药那一刻起,心率关于时间的一个可能的图象为
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com