
2.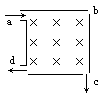 如图所示,正方形容器处在匀强磁场中,一束电子从a孔沿a→b方向垂直射入容器内的匀强磁场中,一部分电子从小孔c射出,一部分电子从小孔d射出。从c、d两孔射出的电子
如图所示,正方形容器处在匀强磁场中,一束电子从a孔沿a→b方向垂直射入容器内的匀强磁场中,一部分电子从小孔c射出,一部分电子从小孔d射出。从c、d两孔射出的电子
A.速度之比vc∶vd=1∶2
B.在容器中运动时间之比tc∶td=1∶1
C.在容器中运动的向心力大小之比Fc∶Fd=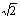 ∶1
∶1
D.在容器中运动的加速度大小之比ac∶ad=2∶1
1.下列正确的叙述是
A.电荷在某处不受电场力作用时,该处的电场强度不一定为零
B.一小段通电导线在某处不受磁场力作用时,该处的磁感强度一定为零
C.在赤道上空沿赤道方向向东发射一束电子流,电子将向下偏转
D.通电导线放在磁场中某处所受磁场力与其长度和电流强度乘积的比等于该处的磁感应强度
10、略解:(1)设AB中点M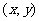 ,联立方程组得:
,联立方程组得: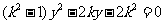 ,则
,则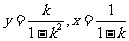 ,消云k得
,消云k得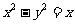 ,注意到△>0,∴
,注意到△>0,∴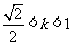 ,得
,得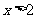
∴AB中点的轨迹方程是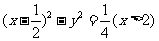 .
.
(2)点Q的轨迹方程是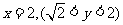 ,是一条线段(无端点).
,是一条线段(无端点).
(3)曲线C的焦点F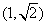 ,设过F的直线方程为
,设过F的直线方程为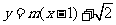 ,与曲线C的方程联立,得弦的中点的横坐标为
,与曲线C的方程联立,得弦的中点的横坐标为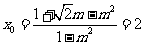 ,解得
,解得 .
.
①当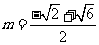 时,弦的中点的纵坐标
时,弦的中点的纵坐标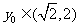 ;②当
;②当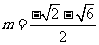 时,弦的中点的纵坐标
时,弦的中点的纵坐标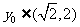 .综上,存在点
.综上,存在点 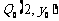 ,使得经过曲线C的焦点的弦被点Q0平分.
,使得经过曲线C的焦点的弦被点Q0平分.
9、解:(1)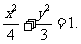 (2)直线m恰为准线,定值即为离心率e.
(2)直线m恰为准线,定值即为离心率e.
(3) 当|PA|=|PB|时,|PA|·|PB|最大。此时点P的坐标为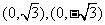
7、②④; 8、②⑤
5、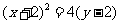 ; 6、A注意焦点所在位置的变化。
; 6、A注意焦点所在位置的变化。
4、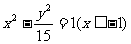 解析:应用圆锥曲线的定义,注意只有一支.
解析:应用圆锥曲线的定义,注意只有一支.
1、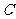 ; 2、
; 2、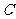 ; 3、
; 3、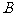 ;
;
2.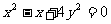 ; 3.
; 3.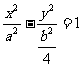 (提示:设
(提示:设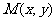 ,则
,则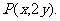 将
将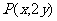 代入双曲线方程得
代入双曲线方程得 。); 4.
。); 4.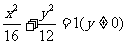 (提示:
(提示: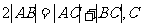 到AB的距离之和为8。)
到AB的距离之和为8。)
[例题探究]
例1.解析设P点的坐标为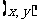 ,则由方程
,则由方程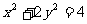 得
得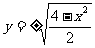 ,
,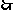 A、B两点的坐标分别为
A、B两点的坐标分别为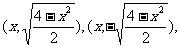 又
又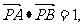
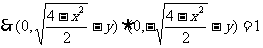 即
即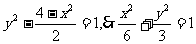 ,又直线
,又直线 与椭圆交于两点,所以
与椭圆交于两点,所以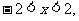 所以点P的轨迹方程为
所以点P的轨迹方程为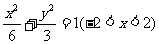 。
。
例2.解析(1)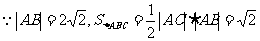 ,
,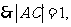 又
又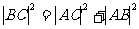 ,从而
,从而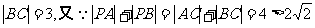 ,所以
,所以
点在以A、B为焦点,长半轴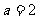 ,半焦距
,半焦距 ,短半轴
,短半轴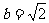 的椭圆
的椭圆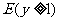 上,
上,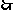 曲线E的方程为
曲线E的方程为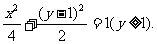
(2)设直线
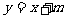 ,代入E的方程,消
,代入E的方程,消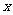 ,可得
,可得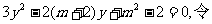
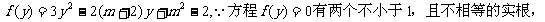 所以有
所以有 解之得
解之得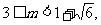 设
设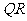 的中点为
的中点为 两点的坐标分别为
两点的坐标分别为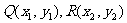 ,
,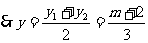
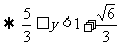 ,将
,将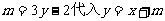 得
得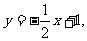 所以
所以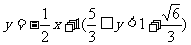 即为M点的轨迹方程。
即为M点的轨迹方程。
例3.解析(1)由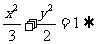 右准线
右准线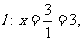 设
设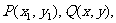 则由
则由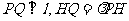 ,得
,得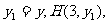 且
且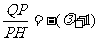 ,
,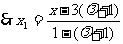 =
=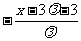 ,故有
,故有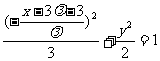 ,即
,即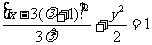 为所求点
为所求点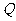 的轨迹G的方程。
的轨迹G的方程。
(2)当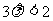 ,即
,即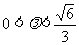 时,轨迹G是焦点在平行于
时,轨迹G是焦点在平行于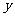 轴的直线上的椭圆,设其焦点
轴的直线上的椭圆,设其焦点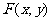 ,则
,则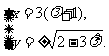 消去
消去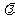 得
得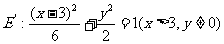
(3)当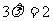 ,即
,即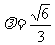 时,轨迹G为圆,其方程为:
时,轨迹G为圆,其方程为: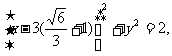 即
即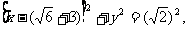 又
又
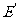 的右准线
的右准线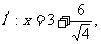 即
即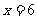
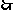 圆心G到准线
圆心G到准线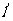 的距离为
的距离为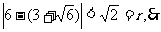 此时G与
此时G与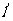 相交。
相交。
例4.解析:(1)直线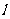 过点
过点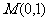 ,当斜率存在时,设其斜率为
,当斜率存在时,设其斜率为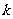 ,则
,则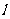 的方程为
的方程为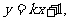 记
记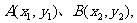 由题设可得点A、B的坐标
由题设可得点A、B的坐标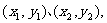 是方程组
是方程组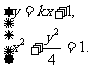 的解,消去
的解,消去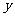 得
得
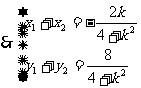 于是
于是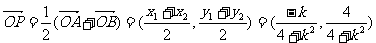 ,设点P的坐标为
,设点P的坐标为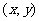 ,则
,则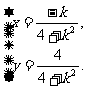 消去参数
消去参数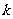 得
得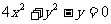 ①当
①当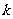 不存在时,A、B中点为坐标原点(0,0),也满足方程①,所以点P的轨迹方程为
不存在时,A、B中点为坐标原点(0,0),也满足方程①,所以点P的轨迹方程为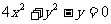 。
。
(3)
由点P的轨迹方程知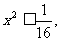 即
即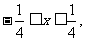
又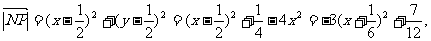 故
故
当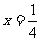 时,
时,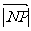 取得最小值为
取得最小值为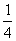 ;
;
当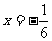 时,
时,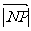 取得最大值为
取得最大值为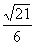 。
。
[冲刺强化训练18]
1.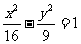 (提示:设动点
(提示:设动点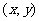 ,则
,则
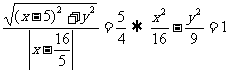 。);
。);
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com