
⒗⑴依题意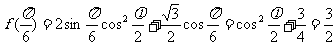 ……2分,
……2分,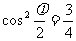 ,因为
,因为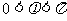 ,
,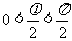 ,所以
,所以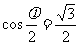 ……3分,
……3分,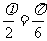 ,
,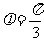 ……4分.
……4分.
⑵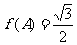 ,即
,即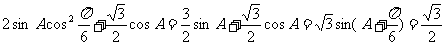
……6分,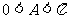 ,
,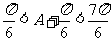 ,所以
,所以 ,
, ……8分,
……8分, 是等腰三角形,
是等腰三角形, ……9分,由正弦定理
……9分,由正弦定理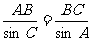 ……11分,得
……11分,得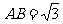 …12分.
…12分.
⒘⑴甲答对(Ⅰ)(Ⅱ)(Ⅲ)三题的概率分别是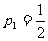 、
、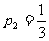 、
、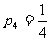 ……1分,
……1分,
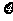 的取值为
的取值为 、
、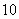 、
、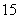 、
、 、
、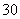 、
、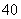 ……2分,
……2分,
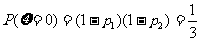 ,
,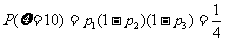 ,
,
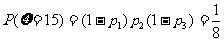 ,
, ,
,
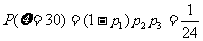 ,
,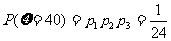 ……8分,
……8分,
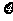
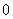
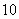
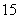

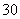
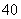
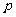

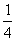

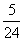
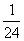
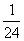
所以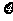 的分布列为
的分布列为
……9分
所以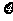 的数学期望
的数学期望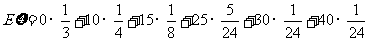
……10分,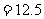 ……11分
……11分
⑵否……12分.
⒙⑴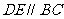 ,
,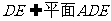 ,
,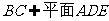 ,所以
,所以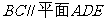 ……2分,因为
……2分,因为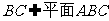 ,
,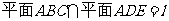 ,所以
,所以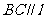 ……3分,所以
……3分,所以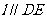 ……4分.
……4分.
⑵取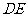 、
、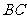 的中点
的中点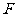 、
、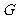 ,连接
,连接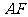 、
、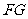 、
、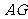 ……5分,因为
……5分,因为 是边长为
是边长为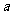 的等边三角形,
的等边三角形,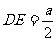 ,所以
,所以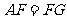 ,
,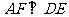 ,
,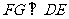 ,从而
,从而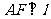 ,
,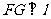 ……
……
6分,所以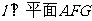 ,
,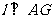 ,
,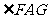 二面角
二面角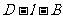 的平面角……8分,在
的平面角……8分,在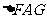 中,因为
中,因为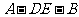 是直二面角,
是直二面角,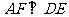 ,所以
,所以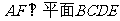 ,
,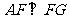 ……9分,又因为
……9分,又因为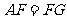 ,所以
,所以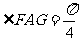 ,即二面角
,即二面角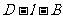 的大小为
的大小为 ……10分.
……10分.
⑶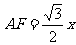 ,
,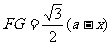 ……11分,四棱锥
……11分,四棱锥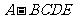 的底面积
的底面积
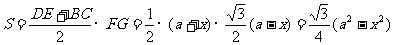 ……12分,
……12分,
四棱锥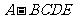 的体积
的体积 ……14分.
……14分.
⒚⑴依题意,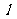 :
: ……1分,不妨设设
……1分,不妨设设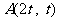 、
、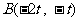 (
(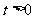 )……2分,
)……2分,
由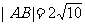 得
得 ,
,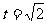 ……3分,所以
……3分,所以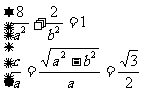 ……5分,
……5分,
解得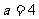 ,
,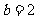 ……6分.
……6分.
⑵由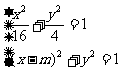 消去
消去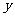 得
得 ……7分,动圆与椭圆没有公共点,当且仅当
……7分,动圆与椭圆没有公共点,当且仅当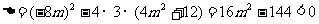 或
或 ……9分,解得
……9分,解得 或
或 ……10分。动圆
……10分。动圆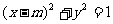 与直线
与直线 没有公共点当且仅当
没有公共点当且仅当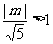 ,即
,即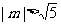 ……12分。解
……12分。解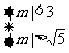 或
或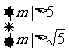 ……13分,得
……13分,得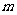 的取值范围为
的取值范围为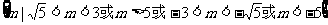 ……14分.
……14分.
⒛⑴设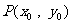 ,
,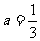 时
时 ,
,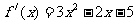 ……1分,直线
……1分,直线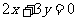 的斜率
的斜率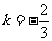 ……2分,依题意
……2分,依题意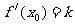 ,即
,即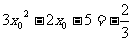
……3分,解得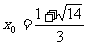 或
或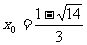 ……4分,所求点为
……4分,所求点为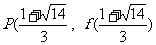 或
或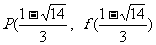 ……6分.
……6分.
⑵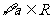 ,
,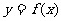 在区间
在区间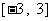 上的图象是连续不断的一条曲线,
上的图象是连续不断的一条曲线, ,
,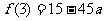 ……7分,
……7分,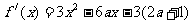 ……8分,解
……8分,解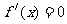 得
得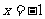 ,
,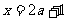 ……9分,
……9分,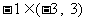 ,
,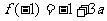 。
。
若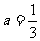 ,则
,则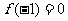 ,
,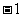 是
是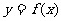 在区间
在区间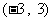 上的一个零点……10分。
上的一个零点……10分。
若 ,则
,则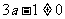 ,
,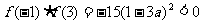 ……12分,
……12分,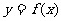 在区间
在区间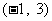 上有零点……13分,因为
上有零点……13分,因为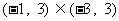 ,所以函数
,所以函数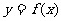 在区间
在区间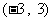 存在零点……14分.
存在零点……14分.
21⑴由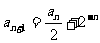 得
得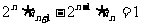 ……2分,
……2分,
所以数列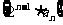 是首项为
是首项为 、公差为
、公差为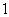 的等差数列……4分,
的等差数列……4分,
所以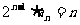 ……5分,
……5分,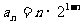 ……6分
……6分
⑵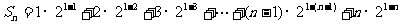
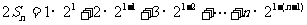 ……8分
……8分
两式相减得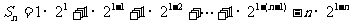 ……9分,
……9分,
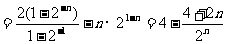 ……11分,
……11分,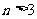 ,
,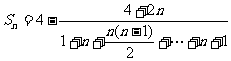
……12分,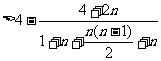 ……13分,
……13分,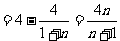 ……14分.
……14分.
⒔ ; ⒕
; ⒕ ; ⒖
; ⒖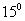 .
.
⒗(本小题满分12分)已知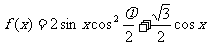 (
( 是常数,
是常数,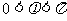 ),
),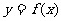 的图象经过点
的图象经过点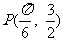 .
.
⑴求 的值;
的值;
⑵在等腰 中,
中,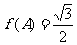 ,
,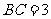 ,求
,求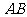 .
.
⒘(本小题满分12分)某个猜答案游戏,组织者将提出相互独立的三个选择题,每题有四个选项,其中只有一个是正确的,游戏规定前两个选择题至少答对一个才有资格答第三题。甲将回答的(Ⅰ)(Ⅱ)(Ⅲ)三题的分值分别是10、15、15,根据自己的知识经验,甲可以排除(Ⅰ)题的2个错误选项、排除(Ⅱ)题的1个错误选项,不能排除(Ⅲ)题的错误选项。假设甲在每题剩下选项中随机选择,三题所得总分为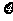 。
。
⑴若组织者按(Ⅰ)(Ⅱ)(Ⅲ)的顺序出题,求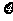 的分布列和数学期望;
的分布列和数学期望;
⑵若组织者不按(Ⅰ)(Ⅱ)(Ⅲ)的顺序出题,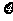 的数学期望是否都相等?
的数学期望是否都相等?
(第⑵问共1分,直接写出“是”或“否”即可,不必具体计算)
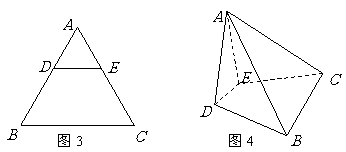
⒙(本小题满分14分)如图3, 是边长为
是边长为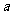 的等边三角形,
的等边三角形,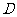 、
、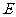 分别是
分别是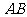 、
、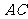 边上一点,
边上一点,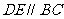 。将
。将 沿
沿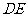 折成直二面角
折成直二面角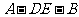 ,连接
,连接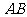 、
、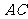 ,得到四棱锥
,得到四棱锥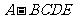 (如图4),其中平面
(如图4),其中平面 与平面
与平面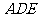 相交于直线
相交于直线 .
.
⑴求证: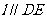 ;
;
⑵若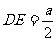 ,求二面角
,求二面角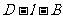 的大小;
的大小;
 ⑶若
⑶若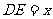 ,求四棱锥
,求四棱锥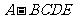 的体积
的体积 .
.
⒚(本小题满分14分)已知椭圆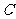 :
: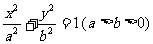 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为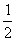 的直线
的直线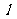 与
与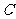 相交于
相交于 、
、 ,
,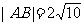 .
.
⑴求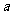 、
、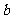 的值;
的值;
⑵若动圆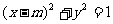 与椭圆
与椭圆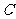 和直线
和直线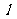 都没有公共点,试求
都没有公共点,试求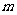 的取值范围.
的取值范围.
⒛(本小题满分14分)已知函数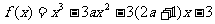 ,
,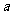 是常数.
是常数.
⑴若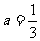 ,曲线
,曲线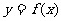 上点
上点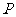 处的切线与直线
处的切线与直线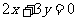 平行,求点
平行,求点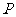 的坐标;
的坐标;
⑵试证明,对任意常数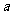 ,函数
,函数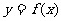 在区间
在区间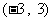 存在零点.
存在零点.
21(本小题满分14分)已知数列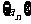 ,
,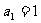 ,对任意
,对任意 ,
,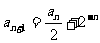 .
.
⑴求数列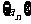 的通项公式;
的通项公式;
⑵设数列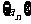 的前
的前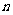 项和为
项和为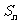 ,试证明:
,试证明: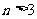 时,
时,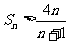 .
.
理科数学评分参考
 ㈠必做题(9-13题)
㈠必做题(9-13题)
⒐平面向量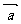 、
、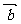 中,
中,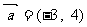 ,
, ,
,
则向量 .
.
⒑在阳光体育活动中,全校学生积极参加室外跑步。
高三⑴班每个学生上一个月跑步的路程从大到小
排列依次是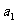 、
、 、
、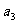 、…、
、…、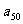 (任意
(任意 、
、
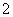 、…、
、…、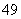 ,
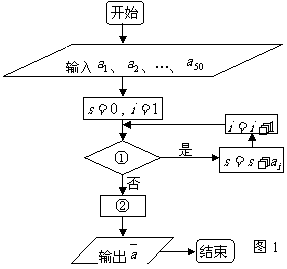
, ),图1是统计该班上一个
),图1是统计该班上一个
月跑步长度前10名学生平均跑步路程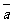 的程序框图。
的程序框图。
则图中判断框①应填 ,处理框(执行框)②应填 .

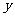
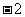
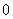
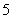
⒒从圆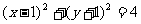 外一点
外一点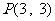 作这个圆的切线,设两条切线之间所夹的角为
作这个圆的切线,设两条切线之间所夹的角为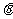 ,则
,则 .
.
⒓对于具有线性相关关系的一组数据:
用最小二乘法求得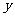 关于
关于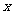 的线性回归方程
的线性回归方程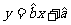 经过一点(样本中心点)
经过一点(样本中心点)
是 .
⒔不等式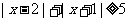 的解集是
.
的解集是
.
㈡选做题(14、15题,考生只能从中选做一题)
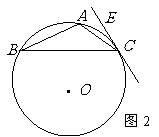 ⒕(坐标系与参数方程选做题)在以
⒕(坐标系与参数方程选做题)在以 为极点的极坐标系中,直线
为极点的极坐标系中,直线 的极坐标方程是
的极坐标方程是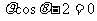 ,直线
,直线 与极轴相交于点
与极轴相交于点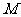 ,以
,以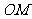
为直径的圆的极坐标方程是 。
⒖(几何证明选讲选做题)如图2, 是圆
是圆 的内接
的内接
三角形,圆 的半径
的半径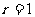 ,
,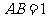 ,
, ,
,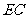
是圆 的切线,则
的切线,则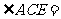 .
.
⒈已知集合 ,
,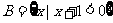 ,则集合
,则集合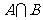 的元素的个数是
的元素的个数是
A. 个 B.
个 B.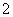 个 C.
个 C.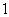 个 D.
个 D.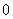 个
个
⒉已知复数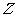 的共轭复数
的共轭复数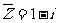 (其中
(其中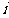 是虚数单位),则
是虚数单位),则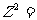
A.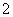 B.
B.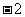 C.
C.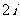 D.
D.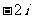
⒊已知函数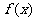 是定义在
是定义在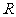 上的奇函数,当
上的奇函数,当 时,
时,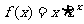 .则当
.则当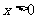 时,
时,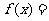
A.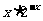 B.
B. C.
C.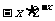 D.
D.
⒋数列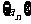 的前
的前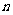 项和为
项和为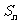 ,已知
,已知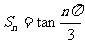 ,则
,则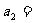
A.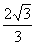 B.
B.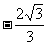 C.
C.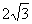 D.
D.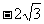
⒌给定下列四个命题:
①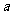 、
、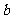 是两异面直线,那么经过直线
是两异面直线,那么经过直线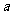 可以作无数个与直线
可以作无数个与直线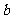 平行的平面。
平行的平面。
②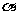 、
、 是任意两个平面,那么一定存在平面
是任意两个平面,那么一定存在平面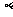 ,满足
,满足 且
且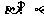 。
。
③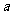 、
、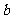 是长方体互相平行的两条棱,将长方体展开,那么在展开图中,
是长方体互相平行的两条棱,将长方体展开,那么在展开图中,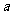 、
、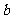 对应的线段所在直线互相平行。
对应的线段所在直线互相平行。
④已知任意直线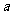 和平面
和平面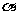 ,那么一定存在平面
,那么一定存在平面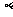 ,满足
,满足 且
且 。
。
其中,为真命题的是
A.①和② B.②和③ C.③和④ D.②和④
⒍在平面直角坐标系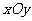 中,点
中,点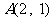 ,
,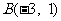 ,则
,则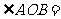
A.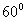 B.
B.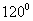 C.
C.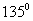 D.
D.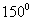
⒎防疫站有A、B、C、D四名内科医生和E、F两名儿科医生,现将他们分成两个3人小组分别派往甲、乙两地指导疾病防控。两地都需要既有内科医生又有儿科医生,而且A只能去乙地。则不同的选派方案共有
A.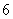 种 B.
种 B.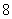 种 C.
种 C. 种 D.
种 D.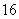 种
种
⒏在平面直角坐标系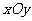 中,不等式组
中,不等式组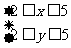 确定的平面区域为
确定的平面区域为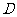 ,在
,在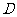 中任取一点
中任取一点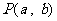 ,则
,则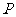 点满足
点满足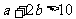 的概率为
的概率为
A.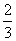 B.
B.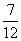 C.
C.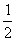 D.
D.
24.(60分)[考查能力]
①对自然、社会和生活的观察与思考的能力及其创造性思维;
②围绕中心选取材料、合理安排结构的能力;
③综合运用多种表达方式(记叙、描写、议论或抒情等)的能力;
④调动语言及知识积累的能力。
23.(6分)本题考查考生准确、鲜明、生动运用语言的能力
[参考答案]示例
数据是标杆,丈量了奔跑攀高的百丈豪情;
图片是画卷,呈现了冲刺飞翔的十分精彩。
(每一句3分:喻体恰当1分,内容准确--围绕运动特点表述1分,鲜明、生动1分)
22.(6分)本题考查考生简明、连贯、得体运用语言的能力
[参考答案]对生存环境的不满意,对本职工作(学习)的不用心,对人际关系(“朋友友谊”或“他人劳动”)的不重视(尊重)
(要求针对“种的是心灵的寂寞,守的是收获的时间,偷的是朋友的情感”的说法,从“相反的”角度作答,且内容不能重复。每一方面2分,内容准确,句子通顺,句式大体相同。如果作答内容没有紧扣“种的是心灵的寂寞,守的是收获的时间,偷的是朋友的情感”,只要能从三个不同方面作答,酌情给分,但最高不能超过4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com