
5.已知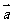 ﹑
﹑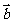 均为非零向量,条件
均为非零向量,条件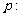
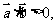 条件
条件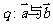 的夹角为锐角,则
的夹角为锐角,则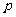 是
是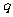 成立的(
)
成立的(
)
A.充要条件 B.充分而不必要的条件
C.必要而不充分的条件 D.既不充分也不必要的条件
4.若不等式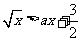 的解集为
的解集为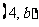 ,则实数
,则实数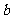 的值为( ).
的值为( ).
A. 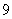 B.
B.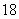 C.36
D.
C.36
D.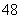

3. 某学校共有2009名学生,将从中选派5名学生在某天去国家大剧院参加音乐晚会,若采
用以下方法选取:先用简单随机抽样从2009名学生中剔除9名学生,再从2000名学生
中随机抽取5名,则其中学生甲被选取的概率是 ( )
A.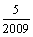 B.
B.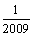 C.
C.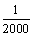 D.
D.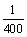

2.已知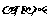 为平面,命题p:若
为平面,命题p:若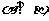
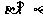 ,则
,则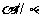 ;命题q:若
;命题q:若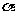 上不共线的三点到
上不共线的三点到 的距离相等,则
的距离相等,则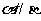 .对以上两个命题,下列结论中正确的是( )
.对以上两个命题,下列结论中正确的是( )
A.命题“p且q”为真 B.命题“p或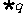 ”为假
”为假
C.命题“p或q”为假 D.命题“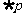 ”且“
”且“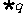 ”为假
”为假
1.直线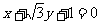 的倾斜角是 ( )
的倾斜角是 ( )
A. 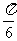 B.
B. 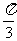 C.
C. 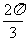 D.
D.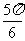

21. (本小题满分14分)
设函数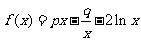 ,且
,且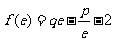 (
(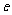 为自然对数的底数).
为自然对数的底数).
(Ⅰ)求实数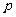 与
与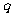 的关系;
的关系;
(Ⅱ)若函数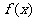 在其定义域内为单调函数,求实数
在其定义域内为单调函数,求实数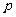 的取值范围;
的取值范围;
(Ⅲ)设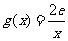 ,若存在
,若存在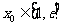 ,使得
,使得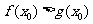 成立,求实数
成立,求实数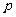 的取值范围.
的取值范围.
|
湖北省赤壁一中高三年级3月质量检测
20.(本小题满分13分)
已知数列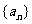 满足:
满足: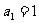 且
且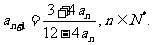
(Ⅰ)若数列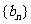 满足:
满足: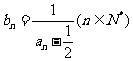 ,试证明数列
,试证明数列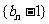 是等比数列;
是等比数列;
(Ⅱ)求数列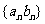 的前
的前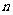 项和
项和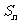 ;
;
(Ⅲ)数列 是否存在最大项,如果存在求出,若不存在说明理由.
是否存在最大项,如果存在求出,若不存在说明理由.
19.(本小题满分12分)
如图,已知椭圆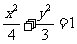 的右焦点为
的右焦点为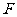 ,过
,过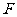 的直线(非
的直线(非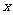 轴)交椭圆于
轴)交椭圆于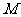 、
、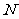 两点,右准线
两点,右准线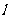 交
交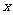 轴于点
轴于点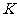 ,左顶点为
,左顶点为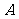
(Ⅰ)求证: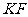 平分
平分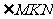 ;
;
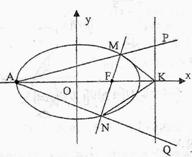 (Ⅱ)直线
(Ⅱ)直线 、
、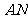 分别交准线
分别交准线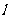 于点
于点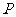 、
、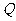 ,设直线
,设直线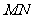 的倾斜角为
的倾斜角为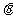 ,试用
,试用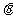 表示线段
表示线段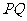 的长度
的长度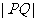 ,并求
,并求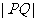 的最小值.
的最小值.
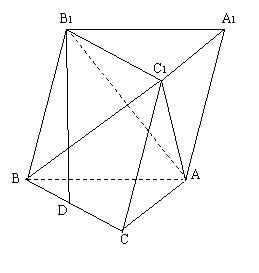
18.(本小题满分12分)
如图,已知斜三棱柱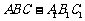 的底面是直角三角形,
的底面是直角三角形,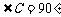 ,侧棱与底面所成的角为
,侧棱与底面所成的角为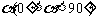 ,点
,点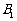 在底面上的射影
在底面上的射影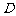 落在
落在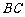 上.
上.
(Ⅰ)若点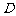 恰为
恰为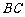 的中点,且
的中点,且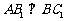 ,求
,求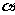 的值.
的值.
 (Ⅱ)若
(Ⅱ)若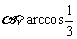 ,且当
,且当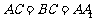 时,求二面角
时,求二面角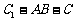 的大小.
的大小.
17.(本小题满分12分)
一个口袋中装有4个红球和5个白球,一次摸奖从中摸两个球,两个球颜色不同则为中奖.
(Ⅰ)试求一次摸奖中奖的概率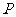 ;
;
(Ⅱ)求三次摸奖(每次摸奖后放回)中奖次数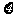 的概率分布列与期望.
的概率分布列与期望.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com