
5、一个棱长都为a的正三棱柱的六个顶点全部在同一个球面上, 则此球的表面积为 ( )
A、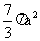 B、
B、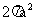 C、
C、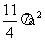 D、
D、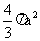
4、如图,正方体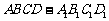 的棱长为
的棱长为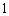 ,点
,点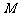 在棱
在棱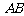 上,
上,
且 ,点
,点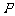 是平面
是平面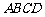 上的动点,且动点
上的动点,且动点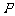 到直线
到直线
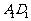 的距离与点
的距离与点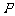 到点
到点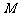 的距离的平方差为
的距离的平方差为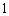 ,则动点
,则动点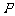 的
的
轨迹是 ( )
A.圆 B.抛物线 C.双曲线 D.直线
3、将半径都为1的4个铅球完全装人形状为正四面体的容品里,这个正四面体的高最小值为 ( )
 A、
A、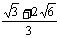 B、
B、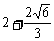 C、
C、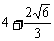 D、
D、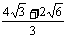
2、在一个45°的二面角的一个面内有一条直线与二面角的棱成45°角,则此直线与二面角的另一个面所成的角为 ( )
A、30° B、45° C、60° D、90°
1.将菱形ABCD沿对角线BD折起,A点变为A',当三棱锥A'-BDC体积最大时,直线A′C与平面BCD所成的角为: ( )
A、90° B、60° C、45° D、30°
3、灵活运用体积法求点面距离,利用空间向量求解空间角与距离时关键是建立恰当空间坐标系,准确得出各点、各向量的坐标,再用相关公式求解空间角与距离。
冲刺强化训练(23)
班级 姓名 学号 成绩
2、借助空间的角的大小可以得到三角形的边的关系,通过向量的坐标运算求角和距离也是一个重要的方法;
1、“三垂线法”是找二面角的平面角常用方法,进而将平面角的计算转化为解直角三角形;
5、半球内有一内接正方体, 正方体的一个面在半球的底面圆内. 若正方体的棱长为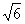 , 则半球的体积为 .
, 则半球的体积为 .
[例题探究]
例1、如图,在四面体P-ABC中, PA=BC=6,PC=AB=10,AC=8,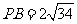 ,F是线段PB上一点,
,F是线段PB上一点,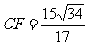 ,点E在线段AB上,且EF⊥PB.
,点E在线段AB上,且EF⊥PB.
(1)求证:PB⊥平面CEF;
 (2)求二面角B-CE-F的大小。
(2)求二面角B-CE-F的大小。
例2. 在四棱锥P-ABCD中,AD⊥AB,CD∥AB,PD⊥底面ABCD,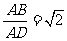 ,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
,直线PA与底面ABCD成60°角,点M、N分别是PA、PB的中点.
 (1)求二面角P-MN-D的大小;
(1)求二面角P-MN-D的大小;
(2)如果△CDN为直角三角形,求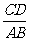 的值.
的值.
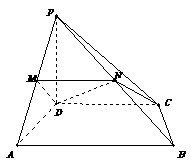
 例3、如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=
例3、如图已知四棱锥P-ABCD,PA⊥平面ABCD,底面ABCD为直角梯形,∠A=90°且AB//CD,AB=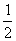 CD.
CD.
(1)点F在线段PC上运动,且设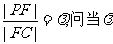 为何值时,BF// 平面PAD?并证明你的结论;
为何值时,BF// 平面PAD?并证明你的结论;
(2)二面角F-CD-B为45°,求二面角B-PC-D的大小;
(3)在(2)的条件下,若AD=2,CD=3,求点A到平面PBC的距离.
[方法点拨]
4、空间四边形ABCD中,E、F分别是AD、BC中点,若AB=1,CD=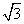 ,AB⊥CD,则EF与CD所成的角为____________
,AB⊥CD,则EF与CD所成的角为____________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com