
20.矩形线框abcd放在匀强磁场中静止不动,磁场方向与线圈平面垂直,磁感应强
度B随时间t变化的图象如图甲所示。设t=0时刻,磁感应强度的方向垂直纸面向
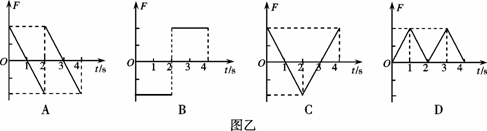
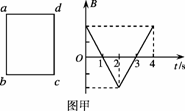 里,则在0-4s时间内,图乙中能正确表示线框ab边所受的安培力F随时间t变化的图象是(规定ab边所受的安培力方向向左为正)
里,则在0-4s时间内,图乙中能正确表示线框ab边所受的安培力F随时间t变化的图象是(规定ab边所受的安培力方向向左为正)
19. 如图所示,一些商场安装了智能化的自动扶梯。为了节约能源,在没有乘客乘行时,自动扶梯以较小的速度匀速运行,当有乘客乘行时自动扶梯经过先加速再匀速两个阶段运行。则电梯在运送乘客的过程中
如图所示,一些商场安装了智能化的自动扶梯。为了节约能源,在没有乘客乘行时,自动扶梯以较小的速度匀速运行,当有乘客乘行时自动扶梯经过先加速再匀速两个阶段运行。则电梯在运送乘客的过程中
A.乘客始终受摩擦力作用
B.乘客经历先超重再失重
C.乘客对扶梯的作用力先指向右下方,再竖直向下
D.扶梯对乘客的作用力始终竖直向上
18.设嫦娥号登月飞船贴近月球表面做匀速圆周运动,测得飞船绕月运行周期为T。飞船在月球上着陆后,自动机器人在月球上做自由落体实验,将某物体由距月球表面高h处释放,经时间t后落到月球表面。已知引力常量为G,由以上数据不能求出的物理量是
A.月球的半径
B.月球的质量
C.月球表面的重力加速度
D.月球绕地球做匀速圆周运动的向心加速度
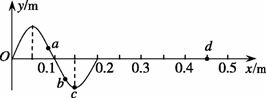
17.如图所示为一列沿x轴正方向传播的简谐横波在t时刻的波形图。已知该波的周期为T,a、b、c、d为沿波传播方向上的四个质点,则下列说法中正确的是
 A.在t+
A.在t+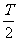 时,质点c的速度达到最大值
时,质点c的速度达到最大值
B.在t +2T时,质点d的加速度达到最大值
C.从t时刻起,质点a比质点b先回到平衡位置
D.从t时刻起,在一个周期内,a、b、c、d四个质点所通过的路程均为一个波长
16.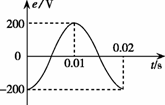 电阻为1Ω的矩形线圈绕垂直于磁场方向的轴在匀强磁场中匀速转动,产生的交变电动势随时间变化的图象如图所示。现把交流电加在电阻为9Ω的电热丝上,则下列说法中正确的是
电阻为1Ω的矩形线圈绕垂直于磁场方向的轴在匀强磁场中匀速转动,产生的交变电动势随时间变化的图象如图所示。现把交流电加在电阻为9Ω的电热丝上,则下列说法中正确的是
A.线圈转动的角速度为31.4rad/s
B.如果线圈转速提高一倍,则电流不会改变
C.电热丝两端的电压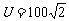 V
V
D.电热丝的发热功率P=1800 W
15.一位高三年级的男生骑着自行车在水平公路上以较快的速度行驶,设所受阻力为车和人总重的0.05倍,则该同学骑车的功率最接近于
A.10W B.50W C.250W D.1kW
14.如图所示,细光束AO以45°的入射角从某种介质射向空气时,分成a、b两束,a光频率为ν1,b光频率为v2。关于这两种单色光,下列说法中正确的是
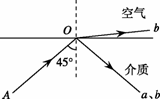 A.从该介质射向空气时,a光发生全反射时的临界角一定大于45°
A.从该介质射向空气时,a光发生全反射时的临界角一定大于45°
B.该介质对b光的折射率一定小于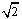
C.用a光和b光分别做双缝干涉实验,若实验条件相同,
则b光在屏上形成的明条纹的间距较小
D.若用a光照射某金属板能发生光电效应,则用b光照射
该金属板也一定能发生光电效应
13.下列说法中不正确的是
A.在α粒子散射实验中,使少数α粒子产生大角度偏转的力是原子核对粒子的库仑斥力
B.氢原子在辐射出一个光子后,核外电子的动能增大
C.已知氦原子的质量m1、电子质量m2、质子质量m3、中子质量m4,则质子和中子在结合成氦核时的质量亏损为(2 m4+2 m3-m1)
D.爱因斯坦狭义相对论的基本结论之一是运动物体长度会收缩,即l =l0 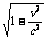 ,它是因时空条件不同而引起的观测效应
,它是因时空条件不同而引起的观测效应
23、(本题5+6+7=18分)设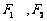 分别是椭圆C:
分别是椭圆C: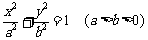 的左右焦点,
的左右焦点,
(1)设椭圆C上的点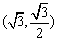 到
到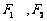 两点距离之和等于4,写出椭圆C的方程和焦点坐标
两点距离之和等于4,写出椭圆C的方程和焦点坐标
(2)设K是(1)中所得椭圆上的动点,求线段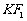 的中点B的轨迹方程
的中点B的轨迹方程
(3)设点P是椭圆C 上的任意一点,过原点的直线L与椭圆相交于M,N两点,当直线PM ,PN的斜率都存在,并记为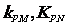 试探究
试探究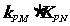 的值是否与点P及直线L有关,并证明你的结论。
的值是否与点P及直线L有关,并证明你的结论。
[解]:(1)由于点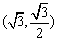 在椭圆上,
在椭圆上,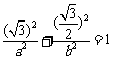 ------1分
------1分
2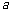 =4,
------2分
=4,
------2分
椭圆C的方程为 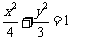 --------4分
--------4分
焦点坐标分别为(-1,0) ,(1,0)-----------5分
(2)设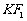 的中点为B(x, y)则点
的中点为B(x, y)则点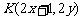 --------7分
--------7分
把K的坐标代入椭圆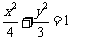 中得
中得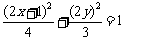 -----10分
-----10分
线段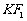 的中点B的轨迹方程为
的中点B的轨迹方程为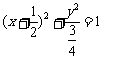 ----------11分
----------11分
(3)过原点的直线L与椭圆相交的两点M,N关于坐标原点对称
设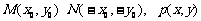 ----12分
----12分
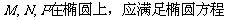 ,得
,得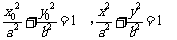 ------13分
------13分
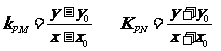 -------------------15分
-------------------15分
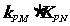 =
=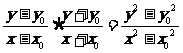 =
=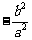 -----------17分
-----------17分
故: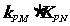 的值与点P的位置无关,同时与直线L无关,-----18分
的值与点P的位置无关,同时与直线L无关,-----18分
22、(本题满分6+10=16分)
在直角坐标系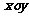 中,已知圆
中,已知圆 的圆心在第二象限,半径为
的圆心在第二象限,半径为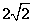 且与直线
且与直线 相切于原点
相切于原点 .椭圆
.椭圆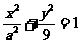 与圆
与圆 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为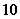 .
.
(1)求圆 的方程;
的方程;
(2)圆 上是否存在点
上是否存在点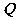 ,使
,使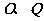 关于直线
关于直线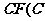 为圆心,
为圆心,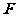 为椭圆右焦点)对称,若存在,请求出点
为椭圆右焦点)对称,若存在,请求出点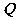 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
答案:解:(1)由题意知:圆心(2,2),半径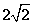 ,圆C:
,圆C:
(2)由条件可知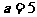 ,椭圆
,椭圆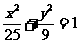 ,
,
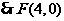
(解法1)若存在,直线CF的方程的方程为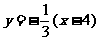 即
即
设Q(x , y),则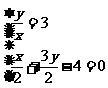 ,
,
解得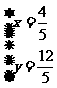 ,所以存在点Q,Q的坐标为
,所以存在点Q,Q的坐标为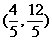 .
.
(解法2)由条件知OF=QF,设Q(x , y),则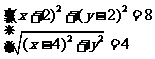 ,
,
解得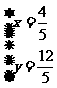 ,所以存在点Q,Q的坐标为
,所以存在点Q,Q的坐标为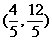
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com