
21.(本题满分12分)
已知椭圆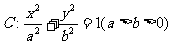 的离心率是
的离心率是 ,若点
,若点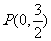 到椭圆
到椭圆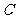 上的点的最远距离为
上的点的最远距离为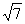 .
.
(Ⅰ)求椭圆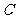 的方程;
的方程;
(Ⅱ)过椭圆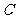 的左焦点
的左焦点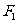 作直线
作直线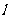 交椭圆
交椭圆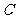 于点
于点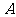 、
、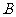 ,且
,且 等于椭圆的短轴长,求直线
等于椭圆的短轴长,求直线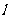 的方程.
的方程.
20.(本题满分12分)
某企业自 年
年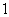 月
月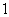 日正式投产,环保监测部门从
日正式投产,环保监测部门从
该企业投产之日起对它向某湖区排放污水进行了四个
月的跟踪监测,检测的数据如下表.并预测,如果不
加以治理,该企业每月向湖区排放污水的量将成等比数列.
|
月份 |
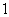 月 月 |
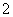 月 月 |
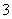 月 月 |
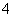 月 月 |
|
该企业向湖区排放的污水(单位:立方米) |
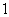 万 万 |
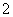 万 万 |
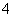 万 万 |
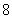 万 万 |
(Ⅰ)如果不加以治理,求从 年
年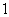 月起,
月起, 个月后,该企业总计向某湖区排放了多少立方米的污水?
个月后,该企业总计向某湖区排放了多少立方米的污水?
(Ⅱ)为保护环境,当地政府和企业决定从7月份开始投资安装污水处理设备,预计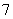 月份的污水排放量比
月份的污水排放量比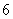 月份减少
月份减少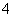 万立方米,以后每月的污水排放量均比上月减少
万立方米,以后每月的污水排放量均比上月减少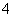 万立方米,当企业停止排放污水后,再以每月
万立方米,当企业停止排放污水后,再以每月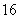 万立方米的速度处理湖区中的污水,请问什么时候可以使湖区中的污水不多于
万立方米的速度处理湖区中的污水,请问什么时候可以使湖区中的污水不多于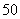 万立方米?
万立方米?
19. (本小题满分12分)
如图是某直三棱柱(侧棱与底面垂直)被削去上底后的
直观图与三视图的侧视图、俯视图,在直观图中,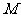 是
是
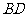 的中点,侧视图是直角梯形,俯视图是等腰直角三
的中点,侧视图是直角梯形,俯视图是等腰直角三
角形,有关数据如图所示.
(Ⅰ)求出该几何体的体积。
(Ⅱ)若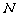 是
是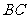 的中点,求证:
的中点,求证: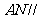 平面
平面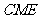 ;
;
(Ⅲ)求证:平面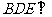 平面
平面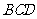 .
.
18.(本小题满分共12分)
已知向量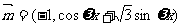 ,
,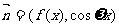 ,其中
,其中 ,且
,且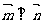 ,又函数
,又函数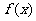 的图象任意两相邻对称轴间距为
的图象任意两相邻对称轴间距为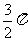 .
.
(Ⅰ)求 的值;
的值;
 (Ⅱ)设
(Ⅱ)设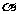 是第一象限角,且
是第一象限角,且 ,求
,求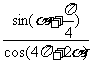 的值.
的值.
17.(本小题满分共12分)
|
序号 (  ) ) |
分组 (分数) |
组中 值 值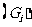 |
频数 (人数) |
频率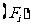 |
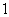 |
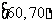 |
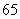 |
① |
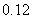 |
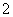 |
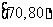 |
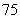 |
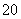 |
② |
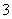 |
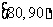 |
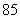 |
③ |
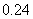 |
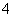 |
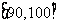 |
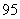 |
④ |
⑤ |
|
合 计 |
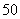 |
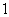 |
 为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有
为了让学生更多的了解“数学史”知识,某中学高二年级举办了一次“追寻先哲的足迹,倾听数学的声音”的数学史知识竞赛活动,共有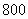 名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为
名学生参加了这次竞赛.为了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为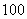 分)进行统计.请你根据频率分布表,解答下列问题:
分)进行统计.请你根据频率分布表,解答下列问题:
(Ⅰ)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);
(Ⅱ)为鼓励更多的学生了解“数学史”知识,成绩不低于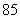 分的同学能获奖,请估计在参加的
分的同学能获奖,请估计在参加的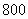 名学生中大概有多少同学获奖?
名学生中大概有多少同学获奖?
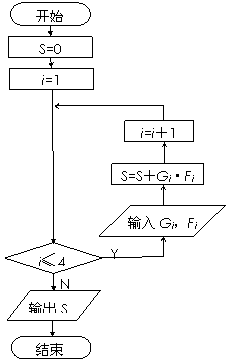
(Ⅲ)在上述统计数据的分析中有一项计算见算法流程图,求输出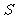 的值.
的值.
16.已知函数错误!不能通过编辑域代码创建对象。错误!不能通过编辑域代码创建对象。,且关于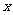 的方程
的方程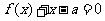 有且只有一个实根,则实数
有且只有一个实根,则实数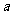 的范围是
.
的范围是
.
15.已知区域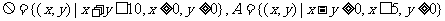 ,若向区域
,若向区域 上随机投
上随机投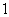 个点,则这个点落入区域
个点,则这个点落入区域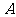 的概率
的概率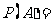 ;
;
14. 已知向量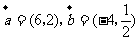 ,直线
,直线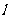 过点
过点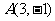 ,且与向量
,且与向量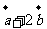 垂直,则直线
垂直,则直线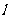 的方程为
的方程为 _______________;
_______________;
13.观察下列式子: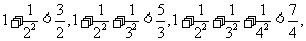 ……,根据以上式子可以猜想:
……,根据以上式子可以猜想: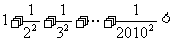 ;
;
12.平面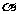 外有两条直线
外有两条直线 和
和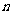 ,如果
,如果 和
和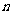 在平面
在平面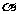 内的射影分别是直线
内的射影分别是直线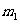 和直线
和直线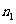 ,给出下列四个命题:
,给出下列四个命题:
①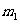 ⊥
⊥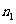

 ⊥
⊥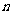 ;
②
;
② ⊥
⊥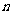

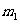 ⊥
⊥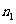 ;
;
③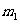 与
与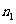 相交
相交
 与
与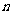 相交或重合; ④
相交或重合; ④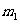 与
与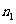 平行
平行
 与
与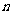 平行或重合;
平行或重合;
其中不正确的命题个数是
A.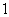
 B.
B. 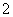 C.
C.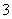 D.
D. 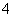
第Ⅱ卷(非选择题 共90分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com