
20.(本题满分13分)
已知函数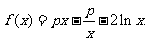
(1)若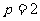 ,求曲线
,求曲线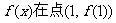 处的切线;
处的切线;
(2)若函数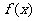 在其定义域内为增函数,求正实数
在其定义域内为增函数,求正实数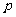 的取值范围;
的取值范围;
(3)设函数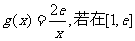 上至少存在一点
上至少存在一点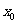 ,使得
,使得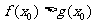 成立,求实数
成立,求实数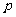 的取值范围。
的取值范围。
19.(本题满分14分)
已知椭圆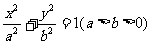 的离心率为
的离心率为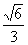 ,短轴的一个端点到右焦点的距离为
,短轴的一个端点到右焦点的距离为 ,直线
,直线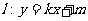 交椭圆于不同的两点A、B。
交椭圆于不同的两点A、B。
(1)求椭圆的方程;
(2)求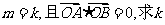 的值(O点为坐标原点);
的值(O点为坐标原点);
(3)若坐标原点O到直线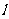 的距离为
的距离为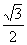 ,求
,求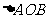 面积的最大值。
面积的最大值。
18.(本题满分13分)
在数列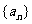 中,
中,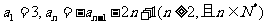
(1)求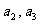 的值;
的值;
(2)证明:数列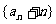 是等比数列,并求
是等比数列,并求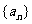 的通项公式;
的通项公式;
(3)求数列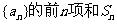 。
。
17.(本题满分14分)
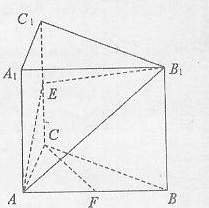 如图,已知直三棱柱ABC-A1B1C1,
如图,已知直三棱柱ABC-A1B1C1, ,E是棱CC1上动点,F是AB中点,
,E是棱CC1上动点,F是AB中点,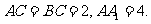
(1)求证: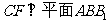 ;
;
(2)当E是棱CC1中点时,求证:CF//平面AEB1;
(3)在棱CC1上是否存在点E,使得二面角
A-EB1-B的大小是45°,若存在,求CE
的长,若不存在,请说明理由。
16.(本题满分13分)
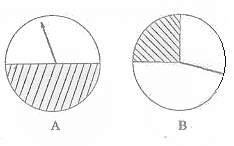
如图,两个圆形转盘A,B,每个转盘阴影部分各占转盘面积的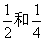 。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
。某“幸运转盘积分活动”规定,当指针指到A,B转盘阴影部分时,分别赢得积分1000分和2000分。先转哪个转盘由参与者选择,若第一次赢得积分,可继续转另一个转盘,此时活动结束,若第一次未赢得积分,则终止活动。
(1)记先转A转盘最终所得积分为随机变量X,则X的取值分别是多少?
(2)如果你参加此活动,为了赢得更多的积分,你将选择先转哪个转盘?请说明理由。
15.(本题满分13分)
在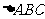 中,角A、B、C所对的边分虽为
中,角A、B、C所对的边分虽为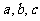 ,且
,且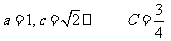
(1)求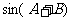 的值;
的值;
(2)求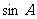 的值;
的值;
(3)求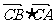 的值。
的值。
14.在数列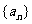 中,若
中,若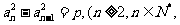
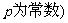 ,则称
,则称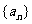 为“等方差数列”,下列是对“等方差数列”的判断;
为“等方差数列”,下列是对“等方差数列”的判断;
①若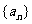 是等方差数列,则
是等方差数列,则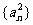 是等差数列;
是等差数列;
②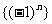 是等方差数列;
是等方差数列;
③若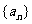 是等方差数列,则
是等方差数列,则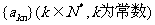 也是等方差数列;
也是等方差数列;
④若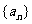 既是等方差数列,又是等差数列,则该数列为常数列。
既是等方差数列,又是等差数列,则该数列为常数列。
其中正确命题序号为 。(将所有正确的命题序号填在横线上)
13.函数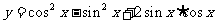 的最小正
的最小正
周期为 ,此函数的值域为 。
12.某校从参加高三年级期末考试的学生中抽出60名学
生,并统计了他们的历史成绩(成绩均为整数且满分
为100分),把其中不低于50分的成绩分成五段
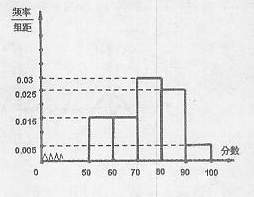
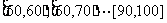 后,画出部分频率分
后,画出部分频率分
布直方图(如图),那么历史成绩在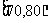 的学
的学
生人数为 。
11.如图,已知PE是圆O的切线,直线PB交圆O于
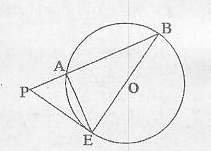 A、B两点,PA=4,AB=12,
A、B两点,PA=4,AB=12,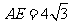 ,则PE的
,则PE的
长为
,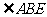 的大小为
。
的大小为
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com