3.(12分)⑴设球B刚进入电场时，带电系统的速度为v1，由动能定理有：k+s-5#u　

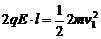　　　 (2分)　　　 解得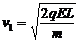：　 (1分)

(2)设带电系统的速度为0时，假设A球仍在电场中，并设B球在电场中的位移为x，

由动能定理有　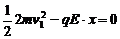　 (2分)　　 解得　 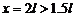(1分)

所以带电系统速度第一次为零时，球A、B应分别在右极板两侧。k+s-5#u　

设A球达到右极板时速度为v，则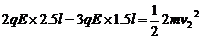： 　　　(2分)

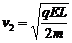解得：(1分)

接下来，只有B球受到电场力，设带电系统的速度为0时，A球相对右极板的位移为x。由动能定理有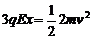：(2分)　　 解得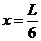：(1分)

2.解：(8分)(1)设滑块到达B点的速度为v，由机械能守恒定律，有　

　　　　　 .

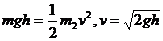(2)滑块在传送带上做匀加速运动，受到传送带对它的滑动摩擦力，有mg =ma,滑块对地位移为L，末速度为v₀，则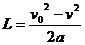，得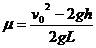

(3)产生的热量等于滑块与传送带之间发生的相对位移中克服摩擦力所做的功，即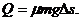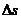为带与滑块间的相对位移，设所用时间为t，则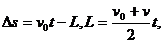，得。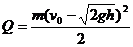

8．(10分)如图17所示，Oxyz为空间直角坐标系，其中Oy轴正方向竖直向上。在整个空间中存在竖直向下的匀强磁场，磁感应强度大小为B。现有一质量为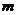、电荷量为q(q＞0)的带电小球从坐标原点O以速度v₀沿Ox轴正方向射出，重力加速度为g，空气阻力可忽略不计。

(1)若在整个空间加一匀强电场，小球从坐标原点O射出恰好做匀速圆周运动，求所加电场的场强大小，以及小球做匀速圆周运动第一次通过z轴的z坐标；

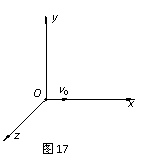(2)若改变第(1)问中所加电场的大小和方向，小球从坐标原点O射出恰好沿Ox轴做匀速直线运动，求此时所加匀强电场的场强大小；k+s-5#u　

(3)若保持第(2)问所加的匀强电场不变而撤去原有的磁场，小球从坐标原点O以速度v₀沿Ox轴正方向射出后，将通过A点，已知A点的x轴坐标数值为x_A，求小球经过A点时电场力做功的功率。

1(8分)解析：(1)设卫星的质量为m,地球的质量为M,　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

在地球表面附近满足 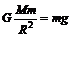　k+s-5#u　

得　　 　　　　①

卫星做圆周运动的向心力等于它受到的万有引力

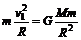　 　　　　　　　　　　　　②

①式代入②式，得到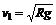

(2)考虑式，卫星受到的万有引力为

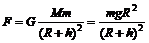　　　　　　　　　 　　③

由牛顿第二定律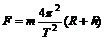　　 ④k+s-5#u　

③、④联立解得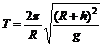

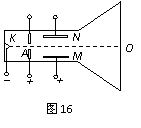
7．(9分)如图16所示为一种测量电子比荷的仪器的原理图，其中阴极K释放电子，阳极A是一个中心开孔的圆形金属板，在AK间加一定的电压。在阳极右侧有一对平行正对带电金属板M、N，板间存在方向竖直向上的匀强电场。O点为荧光屏的正中央位置，且K与O的连线与M、N板间的中心线重合。电子从阴极逸出并被AK间的电场加速后从小孔射出，沿KO连线方向射入M、N两极板间。已知电子从阴极逸出时的初速度、所受的重力及电子之间的相互作用均可忽略不计，在下列过程中，电子均可打到荧光屏上。

(1)为使电子在M、N两极板间不发生偏转，需在M、N两极板间加一个垂直纸面的匀强磁场，请说明所加磁场的方向；

(2)如果M、N极板间的电场强度为E，垂直纸面的匀强磁场的磁感应强度为B，K与A间的电压为U，电子恰能沿直线KO穿过平行金属板，打在荧光屏正中央，求电子的比荷(电荷量和质量之比)为多少；

(3)已知M、N板的长度为L₁，两极板右端到荧光屏的距离为L₂，如果保持M、N极板间的电场强度为E，K与A间的电压为U，而撤去所加的磁场，求电子打到荧光屏上的位置与O点的距离。k+s-5#u　

6．(9分)如图15所示，一小型发电机内有n=100匝矩形线圈，线圈面积S=0.10m²，线圈电阻可忽略不计。在外力作用下矩形线圈在B=0.10T匀强磁场中，以恒定的角速度ω=100π rad/s绕垂直于磁场方向的固定轴OO′匀速转动，发电机线圈两端与R =100Ω的电阻构成闭合回路。求：

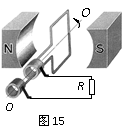(1)线圈转动时产生感应电动势的最大值；k+s-5#u　

(2)从线圈平面通过中性面时开始，线圈转过90º

角的过程中通过电阻R横截面的电荷量；

(3)线圈匀速转动10s，电流通过电阻R产生的焦耳热。

5．(9分)如图14所示，水平光滑绝缘轨道MN的左端有一个固定挡板，轨道所在空间存在E=4.0´10²N/C、水平向左的匀强电场。一个质量m=0.10kg、带电荷量q=5.0´10^-5C的滑块(可视为质点)，从轨道上与挡板相距x₁=0.20m的P点由静止释放，滑块在电场力作用下向左做匀加速直线运动。当滑块与挡板碰撞后滑块沿轨道向右做匀减速直线运动，运动到与挡板相距x₂=0.10m的Q点，滑块第一次速度减为零。若滑块在运动过程中，电荷量始终保持不变，求：

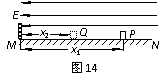(1)滑块沿轨道向左做匀加速直线运动的加速度的大小；

(2)滑块从P点运动到挡板处的过程中，电场力所做的功；

(3)滑块第一次与挡板碰撞的过程中损失的机械能。k+s-5#u　

4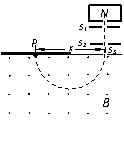．(9分)如图所示为一质谱仪的构造原理示意图，整个装置处于真空环境中，离子源N可释放出质量相等、电荷量均为q(q＞0)的离子。离子的初速度很小，可忽略不计。离子经S₁、S₂间电压为U的电场加速后，从狭缝S₃进入磁感应强度大小为B、方向垂直于纸面向外的匀强磁场中，沿着半圆运动到照相底片上的P点处，测得P到S₃的距离为x。求：

(1)离子经电压为U的电场加速后的动能；

(2)离子在磁场中运动时的动量大小；k+s-5#u　

(3)离子的质量。

3.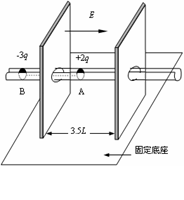如图所示，沿水平方向放置一条平直光滑槽，它垂直穿过开有小孔的两平行薄板，板相距3.5L。槽内有两个质量均为m的小球A和B，球A带电量为+2q，球B带电量为－3q，两球由长为2L的轻杆相连，组成一带电系统。最初A和B分别静止于左板的两侧，离板的距离均为L。若视小球为质点，不计轻杆的质量，在两板间加上与槽平行向右的匀强电场E后(设槽和轻杆由特殊绝缘材料制成，不影响电场的分布)，求：⑴球B刚进入电场时，带电系统的速度大小。⑵带电系统从开始运动到速度第一次为零时球A相对右板的位置。(12分)

2．如图所示，一质量为m的滑块从高为h的光滑圆弧形槽的顶端A处无初速度地滑下，槽的底端B与水平传送带相接，传送带的运行速度为v₀，长为L,滑块滑到传送带上后做匀加速运动，滑到传送带右端C时，恰好被加速到与传送带的速度相同．(12分)

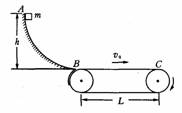求：

(1)滑块到达底端B时的速度v；

(2)滑块与传送带间的动摩擦因数；k+s-5#u　

(3)此过程中，由于克服摩擦力做功而产生的热量Q.

1.(已知地球半径为R，地球表面重力加速度为g，不考虑地球自转的影响。(8分)

(1)推导第一宇宙速度v1的表达式；k+s-5#u　

(2)若卫星绕地球做匀速圆周运动，运行轨道距离地面高度为h，求卫星的运行周期T