
18.(本小题满分13分)
已知函数 其中a为常数,且
其中a为常数,且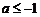 .
.
(Ⅰ)当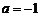 时,求
时,求 在
在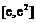 (e=2.718 28…)上的值域;
(e=2.718 28…)上的值域;
(Ⅱ)若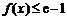 对任意
对任意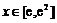 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
17.(本小题满分14分)
如图,三棱柱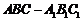 中,侧面
中,侧面
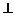 底面
底面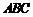 ,
, ,
,
且 ,O为
,O为 中点.
中点.
(Ⅰ)证明: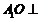 平面
平面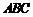 ;
;
(Ⅱ)求直线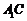 与平面
与平面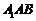 所成角的正弦值;
所成角的正弦值;
 (Ⅲ)在
(Ⅲ)在 上是否存在一点
上是否存在一点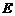 ,使得
,使得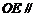 平面
平面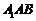 ,若不存在,说明理由;若存在,确定点
,若不存在,说明理由;若存在,确定点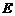 的位置.
的位置.
16.(本小题满分13分)
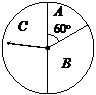
某商场为吸引顾客消费推出一项优惠活动.活动规则如下:消费额每满100元可转动如图所示的转盘一次,并获得相应金额的返券,假定指针等可能地停在任一位置. 若指针停在A区域返券60元;停在B区域返券30元;停在C区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
(Ⅰ)若某位顾客消费128元,求返券金额不低于30元的概率;
(Ⅱ)若某位顾客恰好消费280元,并按规则参与了活动,他获得返券的金额记为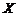 (元).求随机变量
(元).求随机变量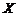 的分布列和数学期望.
的分布列和数学期望.
15.(本小题满分13分)
已知函数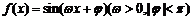 的图象如图所示.
的图象如图所示.
(Ⅰ)求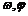 的值;
的值;
(Ⅱ)设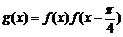 ,求函数
,求函数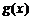 的单调递增区间.
的单调递增区间.

14.在平面直角坐标系中,点集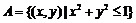 ,
,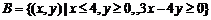 ,
,
则(1)点集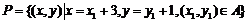 所表示的区域的面积为_____;
所表示的区域的面积为_____;
(2)点集 所表示的区域的面积为 .
所表示的区域的面积为 .
13.已知有公共焦点的椭圆与双曲线中心为原点,焦点在 轴上,左右焦点分别为
轴上,左右焦点分别为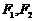 ,且它们在第一象限的交点为P,
,且它们在第一象限的交点为P,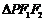 是以
是以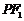 为底边的等腰三角形.若
为底边的等腰三角形.若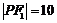 ,双曲线的离心率的取值范围为
,双曲线的离心率的取值范围为 .则该椭圆的离心率的取值范围是 .
.则该椭圆的离心率的取值范围是 .
12.在二项式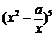 的展开式中,
的展开式中,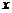 的系数是
的系数是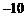 ,则实数
,则实数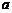 的值为
.
的值为
. 

11.给定下列四个命题:
①“ ”是“
”是“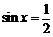 ”的充分不必要条件;
”的充分不必要条件;
②若“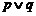 ”为真,则“
”为真,则“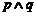 ”为真;
”为真;
③若 ,则
,则 ;
;
④若集合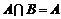 ,则
,则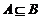 .
.
其中为真命题的是 (填上所有正确命题的序号).
10.如图, 为
为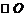 的直径,且
的直径,且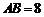 ,P为OA的中点,过P作
,P为OA的中点,过P作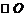 的弦CD,且
的弦CD,且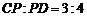 ,则弦CD的长度为 .
,则弦CD的长度为 .
9.某校为了解高三同学寒假期间学习情况,抽查了100名同学,统计他们每天平均学习时间,绘成频率分布直方图(如图).则这100名同学中学习时间在6~8小时内的人数为 _______.
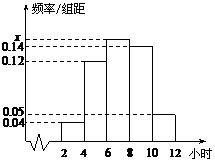

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com