
4.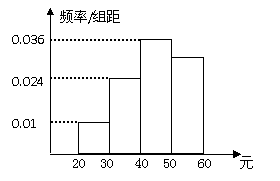 学校为了调查学生在课外读物方面的支出情况,
学校为了调查学生在课外读物方面的支出情况,
抽出了一个容量为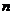 且支出在[20,60)元的样
且支出在[20,60)元的样
本,其频率分布直方图如右图所示,其中支出
在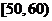 元的同学有
元的同学有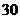 人,则
人,则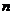 的值为
的值为
A.
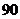 B.
B. 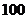
C.
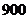 D.
D.
3. 已知集合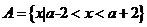 ,
,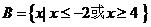 ,则
,则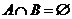 的充要条件是
的充要条件是
A. 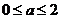 B.
B. 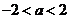 C.
C. 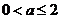 D.
D. 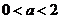
2.
已知变量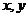 满足
满足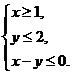 则
则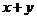 的最小值是
的最小值是
A. 2 B. 3 C. 4 D. 5
项是符合题目要求的。
1.
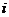 为虚数单位,若
为虚数单位,若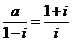 ,则
,则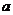 的值为
的值为
A.
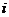 B.
B.
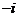 C.
C. 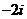 D.
D. 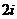
21.(本小题满分12分)本小题主要考察直线、圆、椭圆、直线与圆锥曲线的位置关系等基本
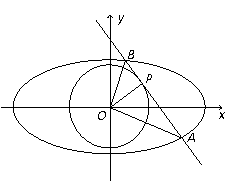 知识. 考察推理论证能力、运算求解能力,考察数形结合思想、化归与转化思想.
知识. 考察推理论证能力、运算求解能力,考察数形结合思想、化归与转化思想.
解:(Ⅰ)依题可得: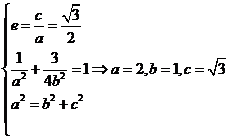
所以椭圆的方程为: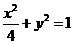 ………………………(4分)
………………………(4分)
(Ⅱ)由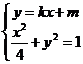 得
得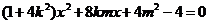


解得: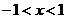 ………………………(7分)
………………………(7分)
(Ⅲ)存在 ………………………(8分)
理由如下:
方程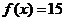 有且只有一个实根即为函数
有且只有一个实根即为函数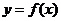 的图象与直线
的图象与直线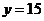 只有一
只有一
个公共点.
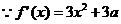
 (1)若
(1)若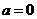 ,则
,则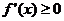 ,
,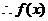 在实数集R上单调递增
在实数集R上单调递增
此时,函数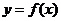 的图象与直线
的图象与直线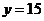 只有一个公共点. ………………(9分)
只有一个公共点. ………………(9分)
(2)若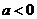 ,则
,则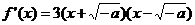 ………………………(10分)
………………………(10分)
列表如下:

20. (本小题满分12分)命题立意:本小题主要考查直线与直线、直线与平面、平面与平面
的位置关系等基础知识,考查了空间想象能力、推理论证能力和运算能力以及化归与转化
能力.
解:(Ⅰ) 在
在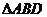 中,
中,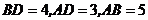
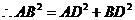
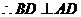 ………………………(2分)
………………………(2分)
又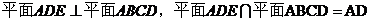
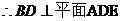
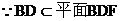

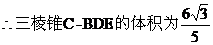 ………………………(12分)
………………………(12分)
18.(本小题满分12分)本小题主要考查概率等基础知识,考查运算求解能力、应用数学知
识分析和解决实际问题的能力。
解:(Ⅰ)因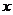 、
、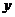 都可取1、2、3、4、5、6,
都可取1、2、3、4、5、6,
故以 为坐标的点共有36个 ………………………(2分)
为坐标的点共有36个 ………………………(2分)


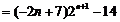 ………………………(12分)
………………………(12分)
22. (本小题满分14分)
已知函数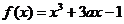 ,
,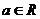 .
.
(Ⅰ)若函数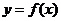 的图象在
的图象在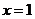 处的切线与直线
处的切线与直线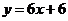 平行,求实数
平行,求实数 的值;
的值;
(Ⅱ)设函数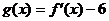 ,对满足
,对满足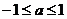 的一切
的一切 的值,都有
的值,都有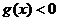 成立,
成立,
求实数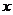 的取值范围;
的取值范围;
(Ⅲ)当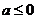 时,请问:是否存在整数
时,请问:是否存在整数 的值,使方程
的值,使方程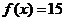 有且只有一个实根?若
有且只有一个实根?若
存在,求出整数 的值;否则,请说明理由.
的值;否则,请说明理由.

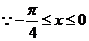 ,
,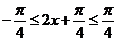
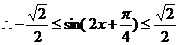
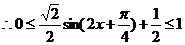 。
。
所以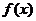 的值域为
的值域为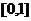 ………………………(12分)
………………………(12分)
21.(本小题满分12分)
已知椭圆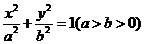 的离心率为
的离心率为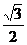 ,点
,点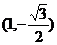 为椭圆上的一点,O为坐标原(Ⅰ)求椭圆的方程;
为椭圆上的一点,O为坐标原(Ⅰ)求椭圆的方程;
(Ⅱ)已知直线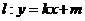 为圆
为圆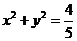 的切线,直线
的切线,直线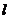 交椭圆于A、B两点,
交椭圆于A、B两点,
求证: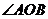 为直角。
为直角。
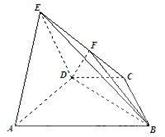
20.(本小题满分12分)
如图,在四棱锥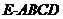 中,
中,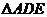 是等边三角形,侧面
是等边三角形,侧面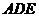 ⊥
⊥
 底面
底面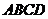 ,其中
,其中
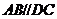 ,
, 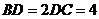 ,
,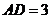 ,
,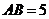
(Ⅰ)若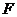 是
是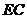 上任一点,求证:平面
上任一点,求证:平面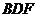 ⊥平面
⊥平面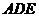 ;
;
(Ⅱ)求三棱锥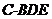 的体积。
的体积。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com