
16、(1)当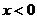 时
时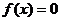 ,当
,当 时,
时,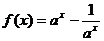 . …………….2分
. …………….2分
由条件可知,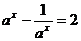 ,即
,即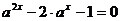 解得
解得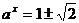 …………6分
…………6分
∵  …………..8分
…………..8分
(2)当 时,
时, ……………10分
……………10分
即 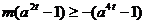

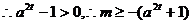 ………………13分
………………13分
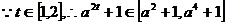
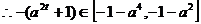
故m的取值范围是 …………….15分
…………….15分
15、 解:(Ⅰ)在Rt△ABC中,AB=1,
解:(Ⅰ)在Rt△ABC中,AB=1,
∠BAC=60°,∴BC=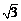 ,AC=2.
,AC=2.
在Rt△ACD中,AC=2,∠CAD=60°,
∴CD=2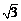 ,AD=4.
,AD=4.
∴SABCD=
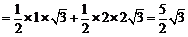 .……………… 3分
.……………… 3分
则V= . ……………… 5分
. ……………… 5分
(Ⅱ)∵PA=CA,F为PC的中点,
 ∴AF⊥PC.
……………… 7分
∴AF⊥PC.
……………… 7分
∵PA⊥平面ABCD,∴PA⊥CD.
∵AC⊥CD,PA∩AC=A,
∴CD⊥平面PAC.∴CD⊥PC.
∵E为PD中点,F为PC中点,
∴EF∥CD.则EF⊥PC. ……… 9分
∵AF∩EF=F,∴PC⊥平面AEF.…… 10分
(Ⅲ)证法一:
取AD中点M,连EM,CM.则EM∥PA.
∵EM 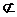 平面PAB,PA
平面PAB,PA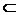 平面PAB,
平面PAB,
∴EM∥平面PAB. ……… 12分
在Rt△ACD中,∠CAD=60°,AC=AM=2,
∴∠ACM=60°.而∠BAC=60°,∴MC∥AB.
∵MC 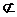 平面PAB,AB
平面PAB,AB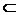 平面PAB,
平面PAB,
∴MC∥平面PAB. ……… 14分
∵EM∩MC=M,
∴平面EMC∥平面PAB.
∵EC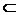 平面EMC,
平面EMC,
∴EC∥平面PAB. ……… 15分
证法二:
延长DC、AB,设它们交于点N,连PN.
∵∠NAC=∠DAC=60°,AC⊥CD,
∴C为ND的中点. ……12分
∵E为PD中点,∴EC∥PN.……14分
∵EC 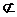 平面PAB,PN
平面PAB,PN 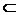 平面PAB,
平面PAB,
∴EC∥平面PAB. ……… 15分
8、60;9、(0,1);10、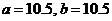 ;11、
;11、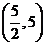 ;12、
;12、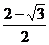 ;13、
;13、 ;14、857.
;14、857.
1、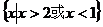 ;2、
;2、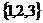 ;3、
;3、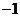 ;4、6
;4、6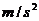 ;5、2;6、-1;7、
;5、2;6、-1;7、 ;
;
16.已知函数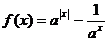 (其中
(其中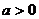 且
且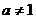 ,
, 为实数常数).(1)若
为实数常数).(1)若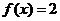 ,求
,求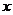 的值(用
的值(用 表示);(2)若
表示);(2)若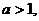 且
且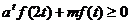 对于
对于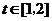 恒成立,求实数m的取值范围(用
恒成立,求实数m的取值范围(用 表示).
表示).
15. 在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
在四棱锥P-ABCD中,∠ABC=∠ACD=90°,∠BAC=∠CAD=60°,PA⊥平面ABCD,E为PD的中点,PA=2AB=2.
(Ⅰ)求四棱锥P-ABCD的体积V;
(Ⅱ)若F为PC的中点,求证PC⊥平面AEF;
(Ⅲ)求证CE∥平面PAB.
14.对于任意实数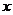 ,符号[
,符号[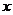 ]表示
]表示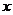 的整数部分,即[
的整数部分,即[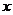 ]是不超过
]是不超过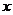 的最大整数”。在实数轴R(箭头向右)上[
的最大整数”。在实数轴R(箭头向右)上[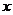 ]是在点
]是在点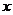 左侧的第一个整数点,当
左侧的第一个整数点,当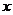 是整数时[
是整数时[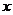 ]就是
]就是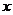 。这个函数[
。这个函数[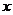 ]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
]叫做“取整函数”,它在数学本身和生产实践中有广泛的应用。
那么 =
.
=
.
13.已知正四棱锥P-ABCD的高为4,侧棱长与底面所成的角为 ,则该正四棱锥的侧面积是
.
,则该正四棱锥的侧面积是
.
12. 如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角
如图所示,四个相同的直角三角形与中间的小正方形拼成的一个边长为2的大正方形,若直角三角形中较小的锐角 ,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是___
.
,现在向该正方形区域内随机地投掷一枚飞镖,飞镖落在小正方形内概率是___
.
11.在平面直角坐标系中,点 的坐标分别为
的坐标分别为 .如果
.如果 是
是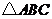 围成的区域(含边界)上的点,那么当
围成的区域(含边界)上的点,那么当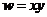 取到最大值时,点
取到最大值时,点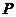 的坐标是
.
的坐标是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com