
22.(本小题满分14分)
(文科)在数列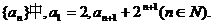
(1)求证:数列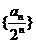 为等差数列;
为等差数列;
(2)若m为正整数,当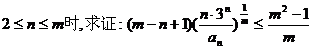
解:(I)由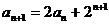 变形得:
变形得: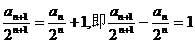
故数列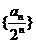 是以
是以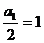 为首项,1为公差的等差数列 (5分)
为首项,1为公差的等差数列 (5分)
(II)(法一)由(I)得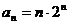
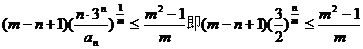 (7分)
(7分)
令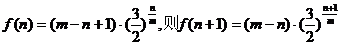
当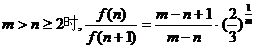
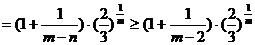
又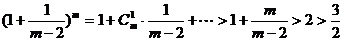
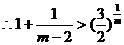
则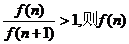 为递减数列。
为递减数列。
当m=n时,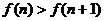
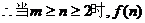 递减数列。 (9分)
递减数列。 (9分)
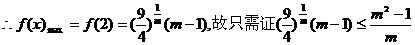
要证: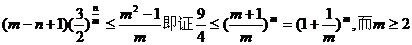 时,
时,
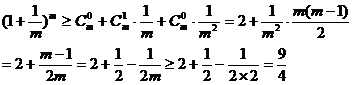
故原不等式成立。 (14分)
(法二)由(I)得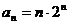
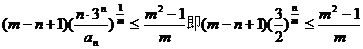 (7分)
(7分)
令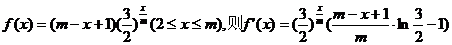
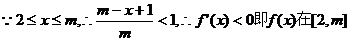 上单调递减。(9分)
上单调递减。(9分)
也即证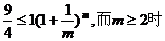 ,
,
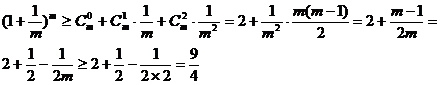
故原不等式成立。 (14分)
(理科)已知数列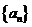 中,
中,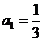 ,当
,当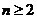 时,其前
时,其前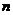 项和
项和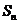 满足
满足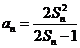 ,
,
(1)
求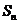 的表达式及
的表达式及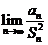 的值;
的值;
(2)
求数列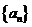 的通项公式;
的通项公式;
(3)
设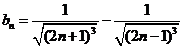 ,求证:当
,求证:当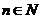 且
且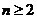 时,
时,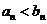 。
。
解:(1)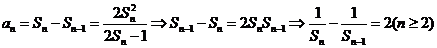
所以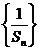 是等差数列。则
是等差数列。则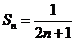 。
。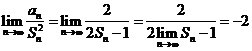 。
。
(2)当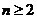 时,
时,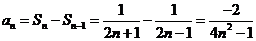 ,综上,
,综上,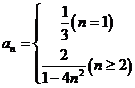 。
。
(3)令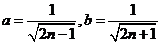 ,当
,当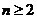 时,有
时,有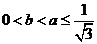 (1)
(1)
法1:等价于求证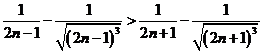 。
。
当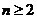 时,
时,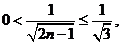 令
令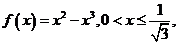
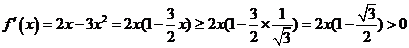 ,则
,则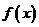 在
在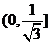 递增。
递增。
又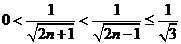 ,所以
,所以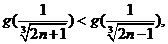 即
即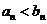 。
。
法(2)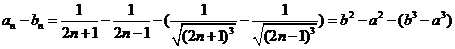
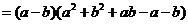 (2)
(2)
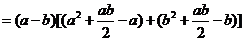
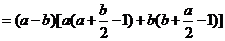 (3)
(3)
因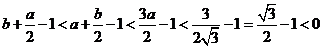
所以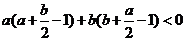
由(1)(3)(4)知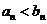 。
。
法3:令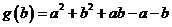 ,则
,则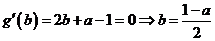
所以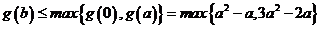
因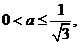 则
则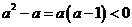
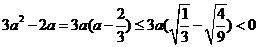
所以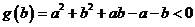 (5) 由(1)(2)(5)知
(5) 由(1)(2)(5)知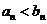
21.(本小题满分12分)
(文科)已知函数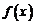 和
和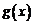 的图象关于原点对称,且
的图象关于原点对称,且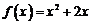 .
.
(Ⅰ)求函数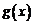 的解析式;
的解析式;
(Ⅱ)解不等式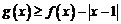 ;
;
(Ⅲ)若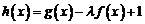 在
在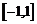 上是增函数,求实数
上是增函数,求实数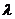 的取值范围.
的取值范围.
解:(Ⅰ)设函数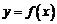 的图象上任意一点
的图象上任意一点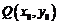 关于原点的对称点为
关于原点的对称点为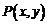 ,则
,则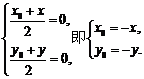
∵点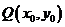 在函数
在函数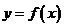 的图象上
的图象上
∴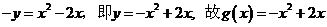
(Ⅱ)由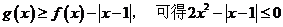
当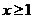 时,
时,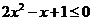 ,此时不等式无解。
,此时不等式无解。
当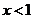 时,
时,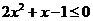 ,解得
,解得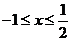 。
。
因此,原不等式的解集为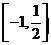 。
。
(Ⅲ)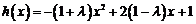
①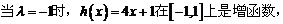
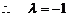
②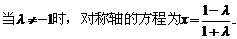
ⅰ)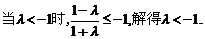
ⅱ)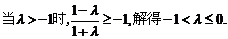
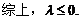
(理科)设函数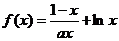 在
在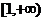 上是增函数。
上是增函数。
(1) 求正实数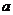 的取值范围;
的取值范围;
(2) 设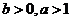 ,求证:
,求证: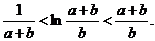
解:(1)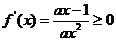 对
对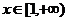 恒成立,
恒成立,
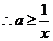 对
对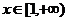 恒成立 又
恒成立 又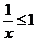
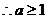 为所求。…………5分
为所求。…………5分
(2)取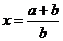 ,
,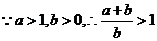 ,
,
一方面,由(1)知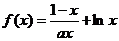 在
在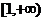 上是增函数,
上是增函数,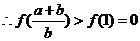
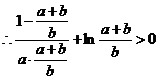 即
即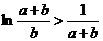 ……………………………………8分
……………………………………8分
另一方面,设函数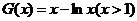
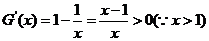
∴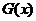 在
在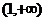 上是增函数且在
上是增函数且在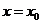 处连续,又
处连续,又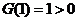
∴当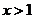 时,
时,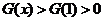
∴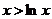 即
即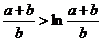
综上所述,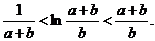 ………………………………………………12分
………………………………………………12分
20.(本小题满分12分)
已知抛物线
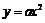 经过点A(2,1),过A作倾斜角互补的两条不同直线
经过点A(2,1),过A作倾斜角互补的两条不同直线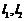 .
.
(Ⅰ)求抛物线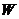 的方程及准线方程;
的方程及准线方程;
(Ⅱ)当直线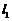 与抛物线
与抛物线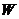 相切时,求直线
相切时,求直线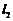 的方程
的方程
(Ⅲ)设直线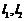 分别交抛物线
分别交抛物线 于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
于B,C两点(均不与A重合),若以线段BC为直径的圆与抛物线的准线相切,求直线BC的方程.
解:(Ⅰ)由于A(2,1)在抛物线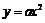 上, 所以
上, 所以 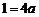 ,即
,即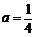 . ………….2分
. ………….2分
故所求抛物线的方程为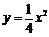 ,其准线方程为
,其准线方程为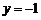 . ……………….3分
. ……………….3分
(Ⅱ)当直线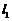 与抛物线相切时,由
与抛物线相切时,由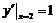 ,可知直线
,可知直线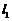 的斜率为1,其倾斜角为
的斜率为1,其倾斜角为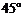 ,所以直线
,所以直线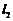 的倾斜角为
的倾斜角为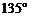 ,故直线
,故直线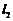 的斜率为
的斜率为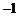 ,所以
,所以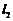 的方程为
的方程为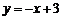 …6分
…6分
(Ⅲ)不妨设直线AB的方程为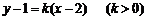 , ………………8分
, ………………8分
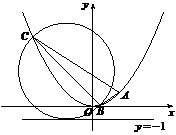 由
由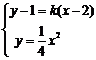 得
得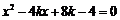 ,……….10分
,……….10分
易知该方程有一个根为2,所以另一个根为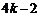 ,
,
所以点B的坐标为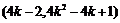 ,
,
同理可得C点坐标为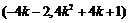 ,
,  ……………….11分
……………….11分
所以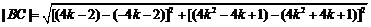

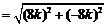
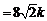 , ……………….9分
, ……………….9分
线段BC的中点为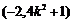 ,因为以BC为直径的圆与准线
,因为以BC为直径的圆与准线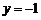 相切,
相切,
所以 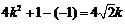 ,由于
,由于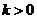 , 解得
, 解得 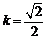 . …………….10分
. …………….10分
此时,点B的坐标为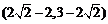 ,点C的坐标为
,点C的坐标为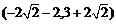 ,
,
直线BC的斜率为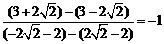 ,
,
所以,BC的方程为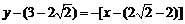 ,即
,即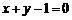 . …….12分
. …….12分
19.(本小题满分12分)
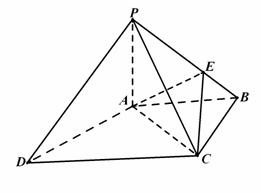 如图,四棱锥
如图,四棱锥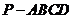 中,
中,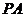 ⊥底面
⊥底面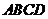 ,底面
,底面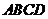 为梯形,
为梯形,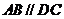 ,
,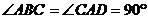 ,且
,且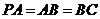 ,点
,点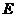 是棱
是棱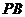 上的动点.
上的动点.
(Ⅰ)当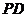 ∥平面
∥平面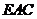 时,确定点
时,确定点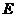 在棱
在棱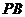 上的位置;
上的位置;
(Ⅱ)在(Ⅰ)的条件下,求二面角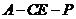 余弦值.
余弦值.
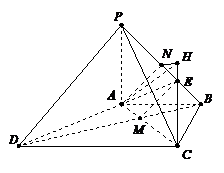 解:(Ⅰ)在梯形
解:(Ⅰ)在梯形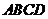 中,由
中,由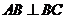 ,
,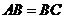 ,得
,得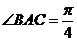 ,∴
,∴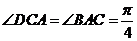 .又
.又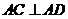 ,故
,故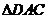 为等腰直角三角形.∴
为等腰直角三角形.∴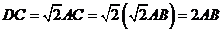 .
.
连接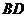 ,交
,交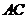 于点
于点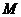 ,则
,则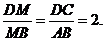
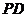 ∥平面
∥平面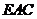 ,又平面
,又平面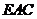
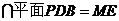 ,∴
,∴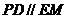
在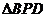 中,
中,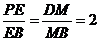 ,
,
即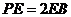 时,
时,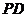 ∥平面
∥平面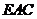
(Ⅱ)方法一:在等腰直角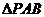 中,取
中,取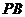 中点
中点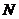 ,连结
,连结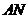 ,则
,则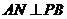 .∵平面
.∵平面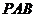 ⊥平面
⊥平面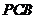 ,且平面
,且平面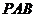
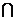 平面
平面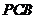 =
=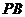 ,∴
,∴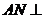 平面
平面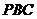 .
.
在平面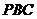 内,过
内,过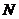 作
作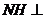 直线
直线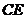 于
于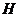 ,连结
,连结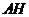 ,由
,由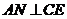 、
、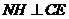 ,得
,得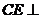 平面
平面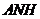 ,故
,故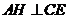 .∴
.∴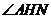 就是二面角
就是二面角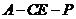 的平面角.
的平面角.
在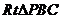 中,设
中,设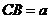 ,则
,则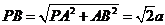 ,
,
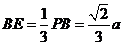 ,
,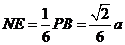 ,
,
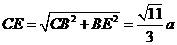 ,
,
由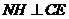 ,
,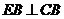 可知:
可知: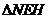 ∽
∽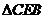 ,∴
,∴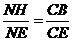 ,
,
代入解得: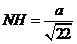 .
.
在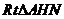 中,
中,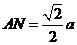 ,∴
,∴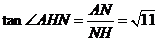 ,
,
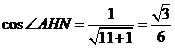 .∴二面角
.∴二面角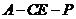 的余弦值为
的余弦值为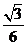 .
.
方法二:以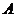 为原点,
为原点,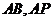 所在直线分别为
所在直线分别为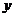 轴、
轴、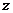 轴,如图建立空间直角坐标系.
轴,如图建立空间直角坐标系.
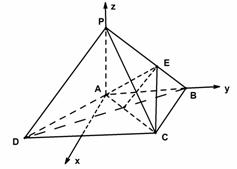 设
设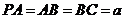 ,则
,则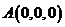 ,
,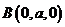 ,
,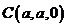 ,
,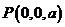 ,
,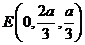 .
.
设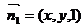 ,为平面
,为平面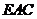 的一个法向量,则
的一个法向量,则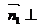
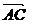 ,
,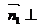
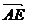 ,∴
,∴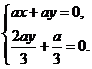 ,解得
,解得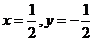 ,∴
,∴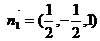 .
.
设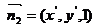 为平面
为平面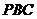 的一个法向量,则
的一个法向量,则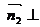
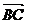 ,
,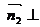
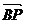 ,
,
又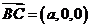 ,
,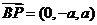 ,∴
,∴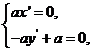 ,解得
,解得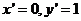 ,∴
,∴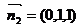 .
.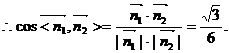
∴二面角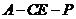 的余弦值为
的余弦值为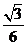 .
.
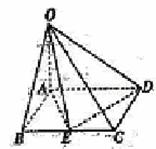
(文科)在四棱锥O-ABCD中,OA⊥平面ABCD,底面ABCD为矩形,AB=OA=tBC(t>0)。
(I)当t=1时,求证:BD⊥DC;
(II)若BC边有且仅有一个点E,使得OE⊥ED,求此时二面角A-CD-E的正切值。
解:(I)当t=1时底面ABCD为正方形,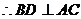
又因为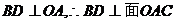
又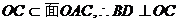 (5分)
(5分)
(II)因为AB,AD,AO两两垂直,分别以它们所在
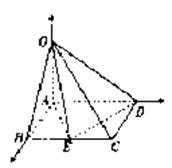 直线为x轴、y轴、z轴建立坐标系,如图所示,令AB=1,
直线为x轴、y轴、z轴建立坐标系,如图所示,令AB=1,
可得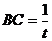
则B(1,0,0),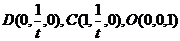 (7分)
(7分)
设BE=m,则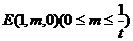
要使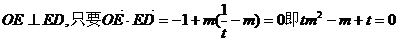
∵BC边有且仅有一个点E,使得OE⊥ED。
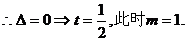
所以BC边上有且仅有一个点E,使得OE⊥ED时,E为BC的中点,且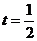
(9分)
设面OED的法向量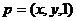
则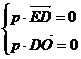 即
即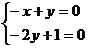 解得
解得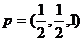
取平面OAD的法向量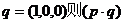 的大小与二面角A-DO-E的大小相等或互补。
所以
的大小与二面角A-DO-E的大小相等或互补。
所以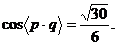
因此二面角A-OD-E的正切值为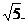 (12分)
(12分)
18.(本小题满分12分)
某商场准备在元旦节期间举行促销活动,根据市场调查,该商场决定从2种服装商品,2种家电商品,3种日用商品中,选出3种商品进行促销活动.
(Ⅰ)试求选出的3种商品中至少有一种是日用商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高150元,同时,若顾客购买该商品,则允许有3次抽奖的机会,若中奖,则每次中奖都获得数额为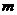 的奖金.假设顾客
的奖金.假设顾客 每次抽奖时获奖与否的概率都是
每次抽奖时获奖与否的概率都是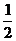 ,请问:商场应将每次中奖奖金数额
,请问:商场应将每次中奖奖金数额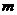 最高定为多少元,才能使促销方案对商场有利?
最高定为多少元,才能使促销方案对商场有利?
解: (Ⅰ)从2种服装商品,2种家电商品,3种日用商品中,选出3种商品一共有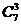 种选法,.选出的3种商品中没有日用商品的选法有
种选法,.选出的3种商品中没有日用商品的选法有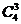 种, 所以选出的3种商品中至少有一种日用商品的概率为
种, 所以选出的3种商品中至少有一种日用商品的概率为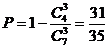 .
……4分
.
……4分
(Ⅱ)顾客在三次抽奖中所获得的奖金总额是一随机变量,设为X,其所有可能值为0 ,
, 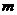 ,2
,2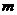 ,3
,3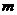 .……5分
.……5分
X=0时表示顾客在三次抽奖中都没有获奖,所以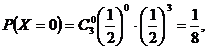 ……6分
……6分
同理可得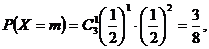 ……7分
……7分
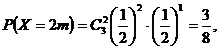 ……8分
……8分
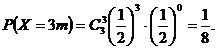 ……9分
……9分
于是顾客在三次抽奖中所获得的奖金总额的期望值是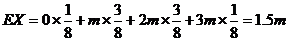 .
. ……10分
……10分
要使促销方案对商场有利 ,应使顾客获奖奖金总额的期望值不大于商场的提价数额,因此应有
,应使顾客获奖奖金总额的期望值不大于商场的提价数额,因此应有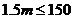 ,所以
,所以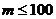 , …… 11分
, …… 11分
故商场应将中奖奖金数额最高定为100元,才能使促销方案对商场有利.… 12分
17.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,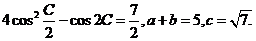
(1)求角C的大小;
(2)求△ABC的面积.
解:(I)由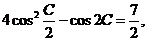 得
得
整理,得 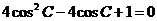 ………………
…………… 4分
………………
…………… 4分
解得 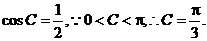 ……………… …6分
……………… …6分
(II)由余弦定理得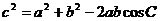 ,
,
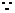
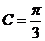 ,
, 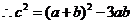 ………………………8分
………………………8分
又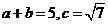 , ∴ab
= 6……………………………10分
, ∴ab
= 6……………………………10分
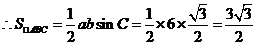 …………………………12分
…………………………12分
16. 给出封闭函数的定义:若对于定义域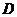 内的任意一个自变量
内的任意一个自变量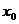 ,都有函数值
,都有函数值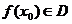 ,则称函数
,则称函数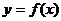 在
在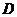 上封闭.若定义域
上封闭.若定义域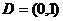 则给出下列函数:
则给出下列函数:
(A)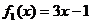 (B)
(B)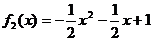
(C)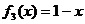 (D)
(D)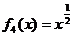
其中在D上封闭的是 .(填序号即可)
答案 BCD
15.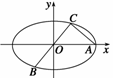 如图所示,已知A、B、C是椭圆E:
如图所示,已知A、B、C是椭圆E: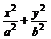 =1(a>b>0)上的三点,,BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.则椭圆的离心率为
=1(a>b>0)上的三点,,BC过椭圆的中心O,且AC⊥BC,|BC|=2|AC|.则椭圆的离心率为
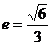
14. 设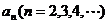 是
是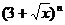 的展开式中
的展开式中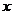 的一次项的系数,则
的一次项的系数,则
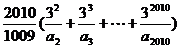 的值是
的值是
答案:18
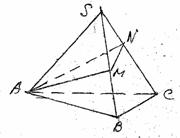
13. 正三棱锥S-ABC的侧棱长为2,侧面等腰三角形的顶角为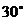 ,过底面顶点作截面
,过底面顶点作截面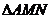 交侧棱SB、SC分别于M、N两点,则
交侧棱SB、SC分别于M、N两点,则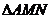 周长的最小值是 。
周长的最小值是 。
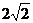
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com