
13. 14.________________________
11.________________________ 12.________________________
(18)(本小题满分14分)在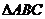 中,角
中,角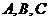 所对应的边分别为
所对应的边分别为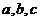 ,
,
且满足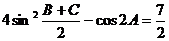 .
.
(I)求角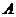 的度数;
的度数;
(II)求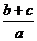 的取值范围.
的取值范围.
(19)(本小题满分14分)某电子科技公司遇到一个技术性难题,决定成立甲、乙两个攻关小组,按要求各自单独进行为期一个月的技术攻关,同时决定对攻关期限内就攻克技术难题的小组给予奖励.已知此技术难题在攻关期限内被甲小组攻克的概率为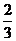 ,被乙小组攻克的概率为
,被乙小组攻克的概率为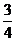 .
.
(I)设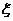 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求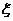 的分布列及
的分布列及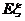 ;
;
(II)设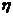 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数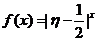 在定义域内单调递增”为事件
在定义域内单调递增”为事件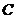 ,求事件
,求事件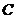 的概率.
的概率.
|
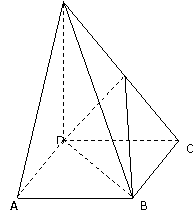
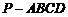 的底面
的底面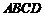 是正方形,侧棱
是正方形,侧棱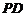 ⊥底面
⊥底面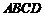 ,
,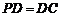 ,
,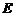 是
是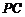 的中点.
的中点.
(I)证明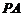 //平面
//平面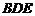 ;
;
|
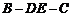 的平面角的余弦值;
的平面角的余弦值;
(III)在棱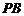 上是否存在点
上是否存在点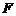 ,使
,使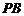 ⊥平面
⊥平面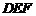 ?
?
若存在,请求出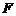 点的位置;若不存在,请说明
点的位置;若不存在,请说明
理由.
(第20题图)
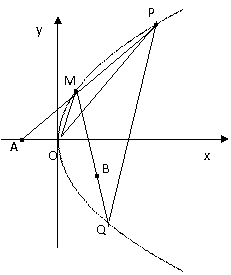 (21)(本小题满分15分)已知点
(21)(本小题满分15分)已知点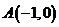 ,
,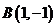 ,抛物线
,抛物线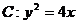 ,
,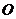 为坐标原点,过点
为坐标原点,过点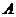 的动直线
的动直线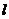 交抛物线
交抛物线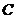 于
于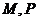 ,直线
,直线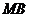 交抛物线
交抛物线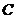 于另一点
于另一点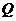 .
.
(I)若向量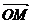 与
与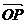 的夹角为
的夹角为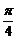 ,求
,求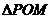 的面积;
的面积;
(II)证明直线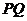 恒过一个定点.
恒过一个定点.
|
(22) (本小题满分15分)已知二次函数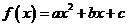 和“伪二次函数”
和“伪二次函数”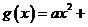
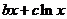 (
(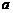 、
、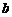 、
、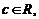
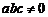 ),
),
(I)证明:只要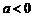 ,无论
,无论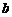 取何值,函数
取何值,函数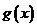 在定义域内不可能总为增函数;
在定义域内不可能总为增函数;
(II)在二次函数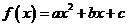 图象上任意取不同两点
图象上任意取不同两点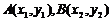 ,线段
,线段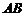 中点的横坐标为
中点的横坐标为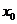 ,记直线
,记直线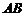 的斜率为
的斜率为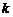 ,
,
(i)求证: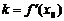 ;
;
(ii)对于“伪二次函数”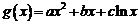 ,是否有(i)同样的性质?证明你的结论.
,是否有(i)同样的性质?证明你的结论.

 台州市2010年高三年级第一次调考试题
台州市2010年高三年级第一次调考试题
数 学(理) 答 题 卷 2010.3
 (11)已知
(11)已知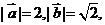
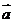 与
与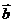 的夹角为45°,若
的夹角为45°,若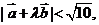 则实数
则实数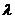 的取值范围 是 ▲ .
的取值范围 是 ▲ .
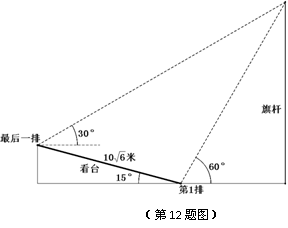
(12)某校运动会开幕式上举行升旗仪式,旗杆正好处在坡度15°的看台的某一列的正前方,从这一列的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,且第一排和最后一排的距离为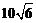 米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以 ▲ (米/秒)的速度匀速升旗.
米(如图所示),旗杆底部与第一排在一个水平面上.若国歌长度约为50秒,升旗手应以 ▲ (米/秒)的速度匀速升旗.
(13) 若实数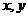 满足不等式组
满足不等式组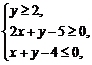 则
则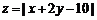 的最小值是 ▲ .
的最小值是 ▲ .
(14)设双曲线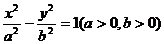 的两个焦点为
的两个焦点为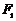 ,
,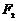 ,若
,若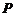 是双曲线上的一点,且
是双曲线上的一点,且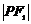 =
= 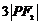 ,则双曲线离心率的取值范围为 ▲ .
,则双曲线离心率的取值范围为 ▲ .
(15)观察下列等式:
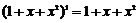 ,
,
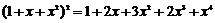 ,
,
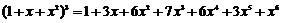 ,
,
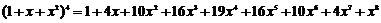 ,
,
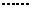
由以上等式推测:
对于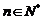 ,若
,若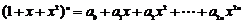 ,则
,则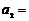 ▲ .
▲ .
(16)反复抛掷一个质地均匀的正方体骰子,依次记录每一次落地时骰子向上的点数,当记有三个不同点数时即停止抛掷. 若抛掷四次恰好停止,则记有这四次点数的所有不同结果的种数为 ▲ .(用数字作答)
(17)已知函数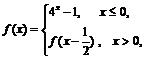 若方程
若方程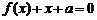 有两个大于零的实数根,
有两个大于零的实数根,
则实数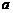 的取值范围是 ▲ .
的取值范围是 ▲ .
(1) “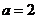 ”是“直线
”是“直线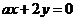 平行于直线
平行于直线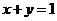 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(2) 若复数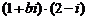 是纯虚数(
是纯虚数(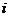 是虚数单位,
是虚数单位,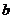 是实数),则
是实数),则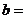
(A)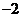 (B)
(B)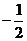 (C)
(C)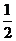 (D)2
(D)2
(3) 设全集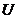 是实数集
是实数集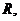
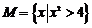 ,
,
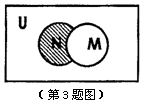
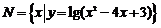 ,则图中阴影部分所表示的集合是
,则图中阴影部分所表示的集合是
(A)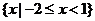 (B)
(B)
(C)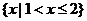 (D)
(D)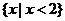
(4)在 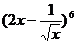 的展开式中的常数项为
的展开式中的常数项为
(A)15 (B)-15 (C)60 (D)- 60
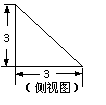
 (5) 一个几何体的三视图及其尺寸如图(单位:cm),
(5) 一个几何体的三视图及其尺寸如图(单位:cm),
则该几何体的体积是
|
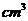 (B)
(B)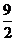
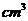
|
 (C)9
(C)9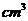 (D)
(D)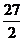
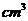
|
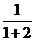 ,
,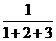 ,
,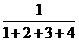 ,
,
…,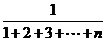 ,…的前
,…的前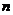 项和为
项和为
(A)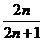 (B)
(B)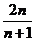 (C)
(C)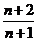 (D)
(D)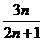
 (7)若直线
(7)若直线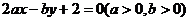 被圆
被圆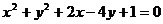 截得的弦长为4,则
截得的弦长为4,则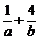 的最小值是
的最小值是
(A)5 (B)6
(C)8 (D)9
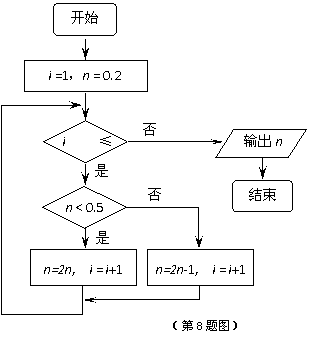
(8)右图所示的算法框图执行后输出的结果是
(A)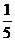 (B)
(B)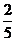
(C)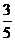 (D)
(D)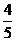
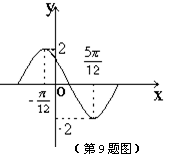 (9)已知函数
(9)已知函数 的导函数
的导函数 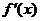 在一个周期内的图象如图所示, 则函数
在一个周期内的图象如图所示, 则函数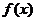 的解析式可以是
的解析式可以是
(A)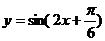 (B)
(B)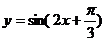
(C)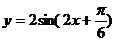 (D)
(D)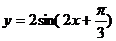
(10)已知各棱长均为1的四面体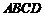 中,
中,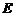 是
是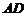 的中点,
的中点,
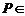 直线
直线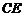 ,则
,则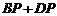 的最小值为
的最小值为
(A)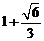 (B)
(B)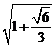 (C)
(C)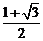 (D)
(D)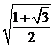
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com