
21.(本小题满分13分)
已知函数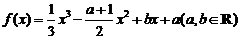 ,其导函数
,其导函数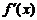 的图象过原点.
的图象过原点.
(1)当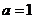 时,求函数
时,求函数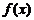 的图象在
的图象在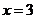 处的切线方程;
处的切线方程;
(2)若存在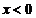 ,使得
,使得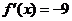 ,求的最大值;
,求的最大值;
(3)当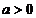 时,确定函数
时,确定函数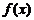 的零点个数.
的零点个数.
宁乡县2010年湖南新课新课标高考仿真试卷
20. (本小题满分13分)
设A(x1,y1),B(x2,y2)是椭圆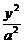 +
+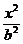 =1(a>b>0)上的两点,已知向量
=1(a>b>0)上的两点,已知向量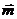 =(
=(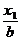 ,
,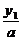 ),
),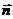 =(
=(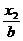 ,
,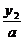 ),若
),若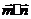 =0且椭圆的离心率e=
=0且椭圆的离心率e=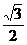 ,短轴长为2,O为坐标原点.
,短轴长为2,O为坐标原点.
(1)求椭圆的方程;
(2)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(3)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
19.(本小题满分13分)在数列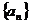 中,
中,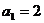 ,
,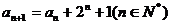
(1)求证:数列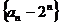 为等差数列;
为等差数列;
(2)设数列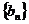 满足
满足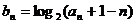 ,
,
若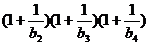 …
…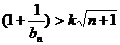 对一切
对一切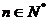 且
且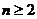 恒成立,求实数
恒成立,求实数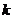 的取值范围。
的取值范围。
18. (本小题满分12分)
(本小题满分12分)
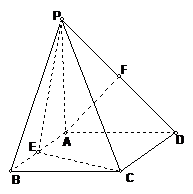
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,
PA=2,∠PDA=45°,点E、F分别为棱AB、PD的中点。
(1)求证:AF∥平面PCE;
(2)求证:平面PCE⊥平面PCD;
17.(本小题满分12分)
袋子中有质地、大小完全相同的4个球,编号分别为1,2,3,4.甲、乙两人玩一种游戏:甲先摸出一个球,记下编号,放回后乙再摸一个球,记下编号,若两个编号的和为奇数算甲赢,否则算乙赢.记基本事件为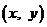 ,其中
,其中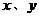 分别为甲、乙摸到的球的编号
分别为甲、乙摸到的球的编号
(1)列举出所有的基本事件,并求甲赢且编号的和为5的事件发生的概率;
(2)比较甲胜的概率与乙胜的概率,并说明这种游戏规则是否公平。(无详细解答过程,不给分)
16. (本小题满分12分)
已知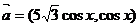 ,
,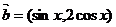 ,其中
,其中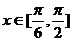 ,设函数
,设函数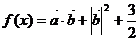 .
.
(1)求函数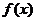 的值域;
的值域;
(2)若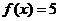 ,求的值.
,求的值.
15.如图,已知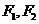 是椭圆
是椭圆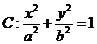
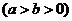 的
的
左、右焦点,点在椭圆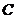 上,线段
上,线段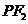 与圆
与圆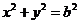
相切于点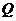 ,且点
,且点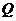 为线段
为线段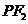 的中点,则椭圆
的中点,则椭圆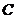 的离心率
的离心率
为 .
14. 若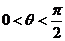 ,由不等式
,由不等式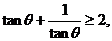
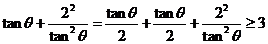
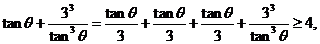 …,启发我们得到推广结论:
…,启发我们得到推广结论:
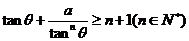 ,则
,则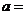 。
。
13. 某化工厂准备对某产品进行技术改良,现决定优选加工温度,试验范围为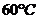 -
-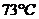 ,精确度要求为
,精确度要求为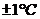 ,现在技术员准备用分数法进行优选,则第一试点的数值是 。
,现在技术员准备用分数法进行优选,则第一试点的数值是 。
12. 已知实数、满足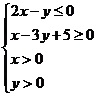 ,则
,则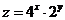 的最大值为
.
的最大值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com