
6.(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
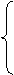 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x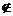 Dg
Dg
g(x) 当x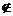 Df且x∈Dg
Df且x∈Dg
(3) 若函数f(x)=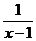 ,g(x)=x2,x∈R,写出函数h(x)的解析式;
,g(x)=x2,x∈R,写出函数h(x)的解析式;
(4) 求问题(1)中函数h(x)的值域;
(3)若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.
[解] (1)h(x)=
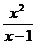 x∈(-∞,1)∪(1,+∞)
x∈(-∞,1)∪(1,+∞)
1 x=1
(2) 当x≠1时, h(x)= 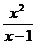 =x-1+
=x-1+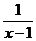 +2,
+2,
若x>1时, 则h(x)≥4,其中等号当x=2时成立 若x<1时, 则h(x)≤ 0,其中等号当x=0时成立
∴函数h(x)的值域是(-∞,0] {1}∪[4,+∞)
(3)令 f(x)=sin2x+cos2x,α=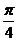
则g(x)=f(x+α)= sin2(x+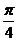 )+cos2(x+
)+cos2(x+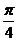 )=cos2x-sin2x,
)=cos2x-sin2x,
于是h(x)= f(x)·f(x+α)= (sin2x+co2sx)( cos2x-sin2x)=cos4x.
另解令f(x)=1+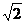 sin2x, α=
sin2x, α=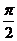 ,g(x)=f(x+α)= 1+
,g(x)=f(x+α)= 1+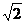 sin2(x+π)=1-
sin2(x+π)=1-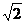 sin2x,
sin2x,
于是h(x)= f(x)·f(x+α)= (1+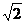 sin2x)( 1-
sin2x)( 1-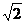 sin2x)=cos4x.
sin2x)=cos4x.
5.已知函数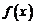 和
和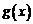 的图象关于原点对称,且
的图象关于原点对称,且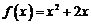 .
.
(Ⅰ)求函数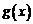 的解析式;
的解析式;
(Ⅱ)解不等式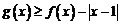 ;
;
(Ⅲ)若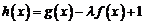 在
在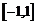 上是增函数,求实数
上是增函数,求实数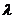 的取值范围.
的取值范围.
解:(Ⅰ)设函数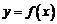 的图象上任意一点
的图象上任意一点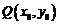 关于原点的对称点为
关于原点的对称点为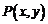 ,则
,则
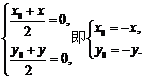
∵点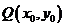 在函数
在函数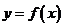 的图象上
的图象上
∴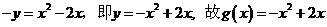
(Ⅱ)由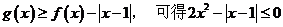
当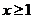 时,
时,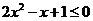 ,此时不等式无解.
,此时不等式无解.
当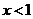 时,
时,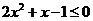 ,解得
,解得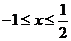 .
.
因此,原不等式的解集为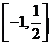 .
.
(Ⅲ)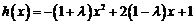
①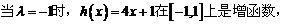
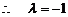
②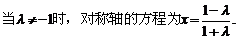
ⅰ)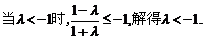
ⅱ)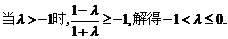
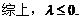
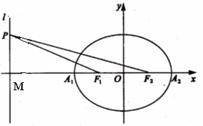
4.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
本题主要考查椭圆的几何性质、椭圆方程、两条直线的夹角等基础知识,考查解析几何的基本思想方法和综合解题能力.满分14分.
解:(Ⅰ)设椭圆方程为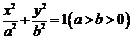 ,半焦距为
,半焦距为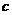 ,则
,则
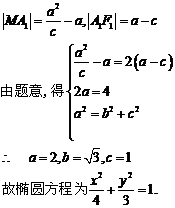
(Ⅱ)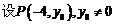
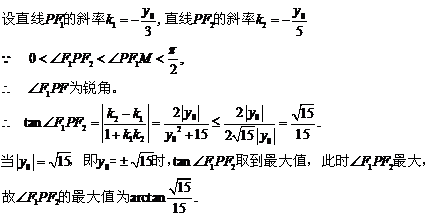
3. 已知不等式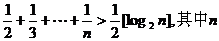 为大于2的整数,
为大于2的整数,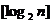 表示不超过
表示不超过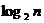 的最大整数. 设数列
的最大整数. 设数列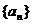 的各项为正,且满足
的各项为正,且满足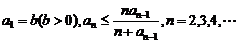
(Ⅰ)证明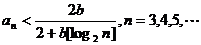
(Ⅲ)试确定一个正整数N,使得当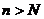 时,对任意b>0,都有
时,对任意b>0,都有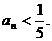
(Ⅰ)证法1:∵当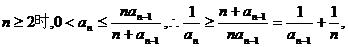
即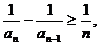
于是有 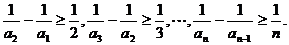
所有不等式两边相加可得 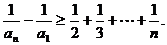
由已知不等式知,当n≥3时有,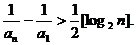
∵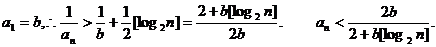
证法2:设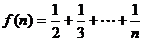 ,首先利用数学归纳法证不等式
,首先利用数学归纳法证不等式
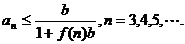
(i)当n=3时, 由 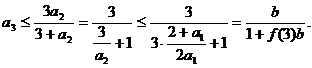
知不等式成立.
(ii)假设当n=k(k≥3)时,不等式成立,即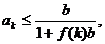
则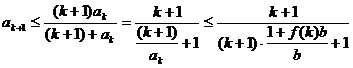
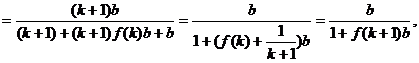
即当n=k+1时,不等式也成立.
由(i)、(ii)知,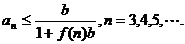
又由已知不等式得 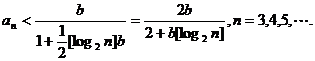
(Ⅲ)∵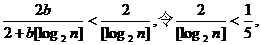
则有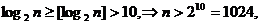
故取N=1024,可使当n>N时,都有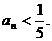
2.设A、B是椭圆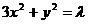 上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
上的两点,点N(1,3)是线段AB的中点,线段AB的垂直平分线与椭圆相交于C、D两点.
(Ⅰ)确定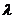 的取值范围,并求直线AB的方程;
的取值范围,并求直线AB的方程;
(Ⅱ)试判断是否存在这样的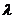 ,使得A、B、C、D四点在同一个圆上?并说明理由.
,使得A、B、C、D四点在同一个圆上?并说明理由.
(Ⅰ)解法1:依题意,可设直线AB的方程为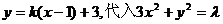 ,整理得
,整理得 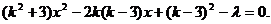 ①
①
设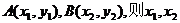 是方程①的两个不同的根,
是方程①的两个不同的根,
∴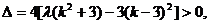 ②
②
且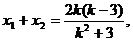 由N(1,3)是线段AB的中点,得
由N(1,3)是线段AB的中点,得
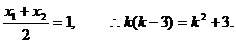
解得k=-1,代入②得,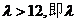 的取值范围是(12,+∞).
的取值范围是(12,+∞).
于是,直线AB的方程为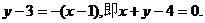
解法2:设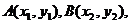 则有
则有
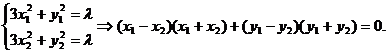
依题意,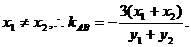
∵N(1,3)是AB的中点, ∴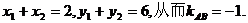
又由N(1,3)在椭圆内,∴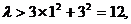
∴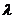 的取值范围是(12,+∞).
的取值范围是(12,+∞).
直线AB的方程为y-3=-(x-1),即x+y-4=0.
(Ⅱ)解法1:∵CD垂直平分AB,∴直线CD的方程为y-3=x-1,即x-y+2=0,
代入椭圆方程,整理得 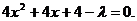
又设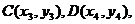 CD的中点为
CD的中点为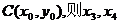 是方程③的两根,
是方程③的两根,
∴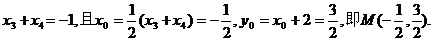
于是由弦长公式可得 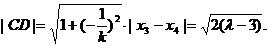 ④
④
将直线AB的方程x+y-4=0,代入椭圆方程得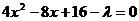 ⑤
⑤
同理可得 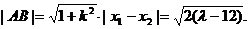 ⑥
⑥
∵当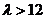 时,
时,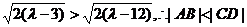
假设存在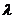 >12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
>12,使得A、B、C、D四点共圆,则CD必为圆的直径,点M为圆心.
点M到直线AB的距离为 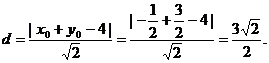 ⑦
⑦
于是,由④、⑥、⑦式和勾股定理可得
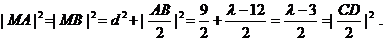
故当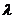 >12时,A、B、C、D四点匀在以M为圆心,
>12时,A、B、C、D四点匀在以M为圆心,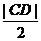 为半径的圆上.
为半径的圆上.
(注:上述解法中最后一步可按如下解法获得:)
A、B、C、D共圆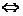 △ACD为直角三角形,A为直角
△ACD为直角三角形,A为直角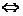 |AN|2=|CN|·|DN|,
|AN|2=|CN|·|DN|,
即 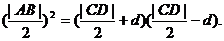 ⑧
⑧
由⑥式知,⑧式左边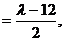
由④和⑦知,⑧式右边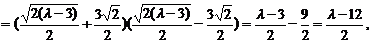
∴⑧式成立,即A、B、C、D四点共圆.
解法2:由(Ⅱ)解法1及λ>12,
∵CD垂直平分AB, ∴直线CD方程为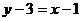 ,代入椭圆方程,整理得
,代入椭圆方程,整理得
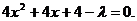 ③
③
将直线AB的方程x+y-4=0,代入椭圆方程,整理得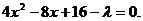 ⑤
⑤
解③和⑤式可得
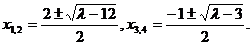
不妨设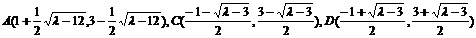
∴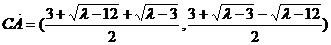
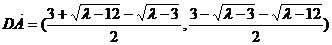
计算可得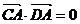 ,∴A在以CD为直径的圆上.
,∴A在以CD为直径的圆上.
又B为A关于CD的对称点,∴A、B、C、D四点共圆.(注:也可用勾股定理证明AC⊥AD)
1. 如图,设抛物线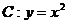 的焦点为F,动点P在直线
的焦点为F,动点P在直线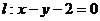 上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
上运动,过P作抛物线C的两条切线PA、PB,且与抛物线C分别相切于A、B两点.
(1)求△APB的重心G的轨迹方程.
(2)证明∠PFA=∠PFB.
解:(1)设切点A、B坐标分别为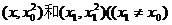 ,
,
∴切线AP的方程为: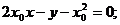
切线BP的方程为: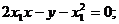
解得P点的坐标为: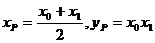
所以△APB的重心G的坐标为 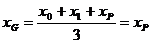 ,
,
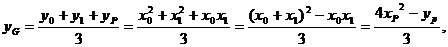
所以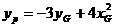 ,由点P在直线l上运动,从而得到重心G的轨迹方程为:
,由点P在直线l上运动,从而得到重心G的轨迹方程为:
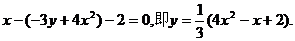
(2)方法1:因为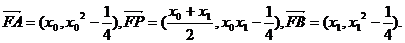
由于P点在抛物线外,则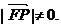
∴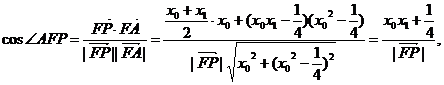
同理有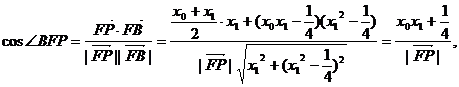
∴∠AFP=∠PFB.
方法2:①当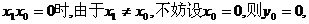 所以P点坐标为
所以P点坐标为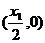 ,则P点到直线AF的距离为:
,则P点到直线AF的距离为: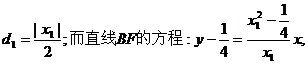
即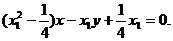
所以P点到直线BF的距离为: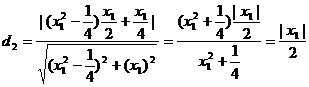
所以d1=d2,即得∠AFP=∠PFB.
②当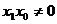 时,直线AF的方程:
时,直线AF的方程: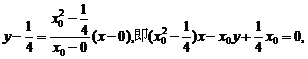
直线BF的方程: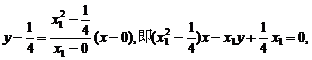
所以P点到直线AF的距离为:
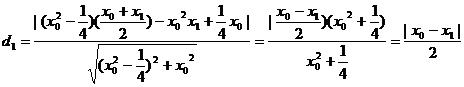 ,同理可得到P点到直线BF的距离
,同理可得到P点到直线BF的距离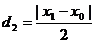 ,因此由d1=d2,可得到∠AFP=∠PFB.
,因此由d1=d2,可得到∠AFP=∠PFB.
6.(本题满分16分)本题共有3个小题,第1小题满分4分, 第2小题满分6分, 第3小题满分6分.
对定义域分别是Df、Dg的函数y=f(x) 、y=g(x),
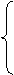 f(x)·g(x) 当x∈Df且x∈Dg
f(x)·g(x) 当x∈Df且x∈Dg
规定: 函数h(x)= f(x)
当x∈Df且x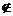 Dg
Dg
g(x) 当x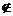 Df且x∈Dg
Df且x∈Dg
(1) 若函数f(x)=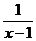 ,g(x)=x2,x∈R,写出函数h(x)的解析式;
,g(x)=x2,x∈R,写出函数h(x)的解析式;
(2) 求问题(1)中函数h(x)的值域;
(3)若g(x)=f(x+α), 其中α是常数,且α∈[0,π],请设计一个定义域为R的函数y=f(x),及一个α的值,使得h(x)=cos4x,并予以证明.
2010年高考数学压轴题系列训练含答案及解析详解六
5.已知函数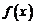 和
和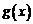 的图象关于原点对称,且
的图象关于原点对称,且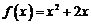 .
.
(Ⅰ)求函数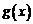 的解析式;
的解析式;
(Ⅱ)解不等式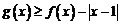 ;
;
(Ⅲ)若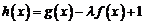 在
在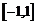 上是增函数,求实数
上是增函数,求实数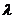 的取值范围.
的取值范围.
4.如图,已知椭圆的中心在坐标原点,焦点F1,F2在x轴上,长轴A1A2的长为4,左准线l与x轴的交点为M,|MA1|∶|A1F1|=2∶1.
 (Ⅰ)求椭圆的方程;
(Ⅰ)求椭圆的方程;
(Ⅱ)若点P为l上的动点,求∠F1PF2最大值.
3. 已知不等式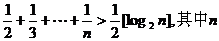 为大于2的整数,
为大于2的整数,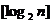 表示不超过
表示不超过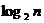 的最大整数. 设数列
的最大整数. 设数列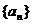 的各项为正,且满足
的各项为正,且满足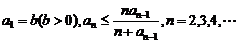
(Ⅰ)证明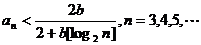
(Ⅲ)试确定一个正整数N,使得当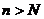 时,对任意b>0,都有
时,对任意b>0,都有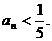
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com