
16.(本小题满分12分)
已知向量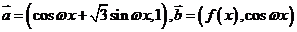 ,其中
,其中 >0,且
>0,且 ,又函数
,又函数 的图像两相邻对称轴之间的距离为
的图像两相邻对称轴之间的距离为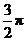 .
.
(1)求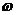 的值;
的值;
(2) 求函数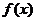 在区间
在区间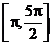 上的最大值与最小值及相应的
上的最大值与最小值及相应的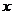 值.
值.
(一)必做题(9-13题.)
9. 一组数据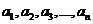 的方差为
的方差为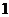 ,则数据
,则数据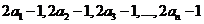 的方差为
的方差为
___________.
10.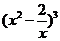 的展开式中的常数项为
.
的展开式中的常数项为
.
11. 已知曲线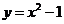 在
在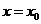 处的切线与曲线
处的切线与曲线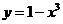 在
在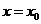 处的切线互相平行,则
处的切线互相平行,则
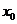 的值为
.
的值为
.
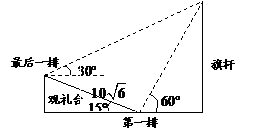
12. 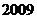 年北京国庆阅兵式上举行升旗仪式.如图,在
年北京国庆阅兵式上举行升旗仪式.如图,在
坡度为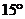 的观礼台上,某一列座位与旗杆在同一个
的观礼台上,某一列座位与旗杆在同一个
垂直于地面的平面上,在该列的第一排和最后一排
测得旗杆顶端的仰角分别为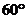 和
和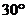 ,且第一排和
,且第一排和
最后一排的距离为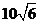 米,则旗杆的高度为 米. 第12题图
米,则旗杆的高度为 米. 第12题图
13. 若不等式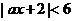 的解集为
的解集为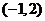 ,则实数
,则实数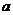 的值为_____________.
的值为_____________.
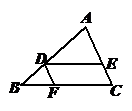 (二)选做题(14、15题,考生只能从中选做一题,两题都选的只计算第14题的得分.)
(二)选做题(14、15题,考生只能从中选做一题,两题都选的只计算第14题的得分.)
14. (几何证明选讲选做题) 如图,在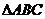 中,
中,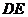 ∥
∥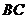 ,
,
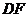 ∥
∥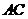 ,
,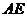 ︰
︰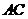 =
=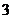 ︰
︰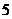 ,
,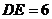 ,则
,则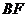 =____.
=____.
第14题图
15. (坐标系与参数方程选做题)若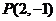 为曲线
为曲线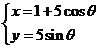 (
(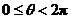 )的弦的中点,则该弦所在直线的普通方程为_____________.
)的弦的中点,则该弦所在直线的普通方程为_____________.
8.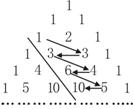 如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以
如图,在杨辉三角形中,斜线l的上方从1按箭头方向可以
构成一个“锯齿形”的数列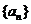 :
: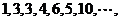 记其前
记其前
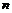 项和为
项和为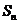 ,则
,则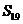 的值为
的值为
A.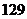 B.
B.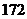 C.
C.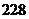 D.
D.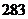 第8题图
第8题图
7. 下列三图中的多边形均为正多边形,M,N是所在边上的中点,双曲线均以图中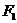 、
、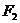 为
为
焦点,且三个图中的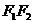 的长相等.设图①②③中双曲线的离心率分别为
的长相等.设图①②③中双曲线的离心率分别为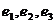 ,则
,则
A.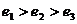 B.
B.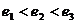 C.
C.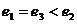 D.
D.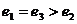
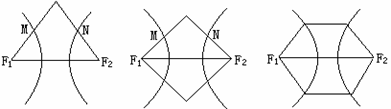
① ② ③
第7题图
6.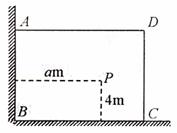 如图,有一直角墙角,两边的长度足够长,在P处有一棵
如图,有一直角墙角,两边的长度足够长,在P处有一棵
树与两墙的距离分别是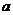 m
m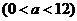 、
、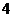 m,不考虑树
m,不考虑树
的粗细.现在想用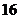 m长的篱笆,借助墙角围成一个矩形
m长的篱笆,借助墙角围成一个矩形
的花圃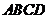 .设此矩形花圃的面积为
.设此矩形花圃的面积为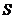
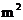 ,
,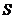 的最大
的最大
值为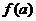 ,若将这棵树围在花圃内,则函数
,若将这棵树围在花圃内,则函数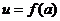 的
的
图象大致是
第6题图
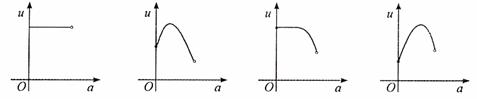
A. B. C. D.
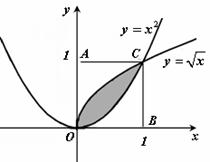
5. 如图所示,在一个边长为1的正方形 内,曲线
内,曲线
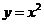 和曲线
和曲线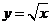 围成一个叶形图(阴影部分),
围成一个叶形图(阴影部分),
向正方形 内随机投一点(该点落在正方形
内随机投一点(该点落在正方形
 内任何一点是等可能的),则所投的点落在
内任何一点是等可能的),则所投的点落在
叶形图内部的概率是
A.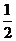 B.
B.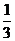 C.
C.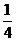 D.
D.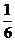 第5题图
第5题图
A.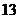 B.
B.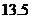
C.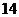 D.
D.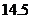
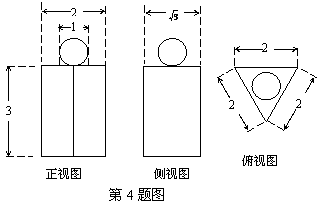
4. 如图为一个几何体的三视图,尺寸如图,则该几何体的表面积为(不考虑接触点)
A.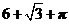 B.
B.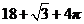 C.
C.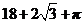 D.
D.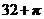
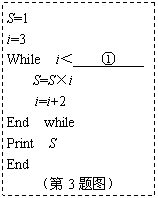
3. 设计一个计算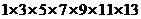 的算法.图中给出了程序
的算法.图中给出了程序
2. 若复数
若复数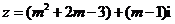 是纯虚数,则实数
是纯虚数,则实数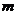 的值为
的值为
A.1 B. 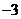 或1 C.
或1 C. 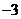 D.
D. 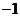 或3
或3
1. 某学校有教师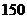 人,其中高级教师
人,其中高级教师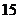 人,中级教师
人,中级教师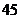 人,初级教师
人,初级教师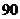 人. 现按职称分层抽样选出
人. 现按职称分层抽样选出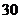 名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为
名教师参加教工代表大会,则选出的高、中、初级教师的人数分别为
A.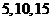 B.
B.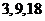 C.
C.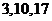 D.
D.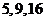
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com