
19. (本题满分14分)
在直角坐标系xOy中,椭圆C1: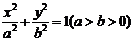 的左、右焦点分别为F1、F2.其中F2也是抛物线C2:
的左、右焦点分别为F1、F2.其中F2也是抛物线C2: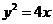 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且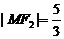 .
.
(1)求C1的方程;
(2)平面上的点N满足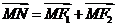 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若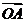 ·
·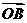 =0,求直线l的方程.
=0,求直线l的方程.
18.(本小题满分14分)
已知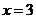 是函数
是函数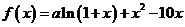 的一个极值点.
的一个极值点.
(Ⅰ)求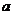 ;
;
(Ⅱ)求函数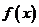 的单调区间;
的单调区间;
(Ⅲ)若直线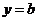 与函数
与函数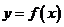 的图象有3个交点,求
的图象有3个交点,求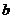 的取值范围.
的取值范围.
17. (本小题满分13分)
甲乙两队参加奥运知识竞赛,每队3人,每人回答一个问题,答对者为本队赢得一分,答错得零分.假设甲队中每人答对的概率均为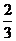 ,乙队中3人答对的概率分别为
,乙队中3人答对的概率分别为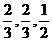 且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.
且各人正确与否相互之间没有影响.用ξ表示甲队的总得分.
(Ⅰ)求随机变量ξ分布列和数学期望;
(Ⅱ)用A表示“甲、乙两个队总得分之和等于3”这一事件,用B表示“甲队总得分大于乙队总得分”这一事件,求P(AB).
15. (本题满分12分)
已知函数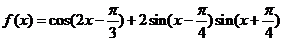
(Ⅰ)求函数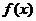 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数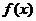 在区间
在区间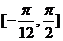 上的值域.
上的值域.
16(本题满分13分)
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=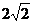 .
.
(Ⅰ)求证: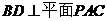 ;
;
(Ⅱ)求二面角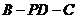 的余弦值;
的余弦值;
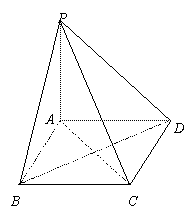 (III)在线段
(III)在线段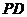 上是否存在一点
上是否存在一点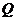 ,使
,使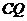 与平面
与平面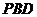 所成的角的正弦值为
所成的角的正弦值为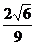 ,若存在,指出点
,若存在,指出点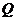 的位置,若不存在,说明理由.
的位置,若不存在,说明理由.
14.给出以下几个命题:
①由曲线y=x2与直线y=2x围成的封闭区域的面积为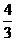 .
.
②已知点A是定圆C上的一个定点,线段AB为圆的动弦,若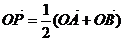 ,
,
O为坐标原点,则动点P的轨迹为圆;
③把5本不同的书分给4个人,每人至少1本,则不同的分法种数为A54·A41=480种.
④若直线l//平面α,直线l⊥直线m,直线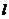
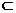 平面β,则β⊥α,其中,正确的命题有
. (将所有正确命题的序号都填在横线上)
平面β,则β⊥α,其中,正确的命题有
. (将所有正确命题的序号都填在横线上)
13. 在平面直角坐标系xOy 中,直线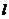 的参数方程为
的参数方程为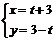 (参数t∈R),圆C的参数方程为
(参数t∈R),圆C的参数方程为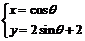 (参数
(参数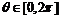 ),则圆C的圆心坐标为_______,圆心到直线
),则圆C的圆心坐标为_______,圆心到直线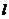 的距离为______.
的距离为______.
12.右面框图表示的程序所输出的结果是_______ .
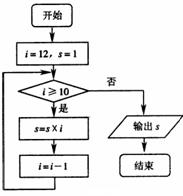

11.一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如下图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在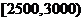 (元)/月收入段应抽出 人.
(元)/月收入段应抽出 人.
10. 如图,平行四边形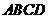 中,
中,
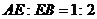 ,若
,若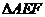 的面积等于1cm
的面积等于1cm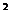 ,
,
则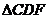 的面积等于 cm
的面积等于 cm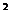 .
.
9.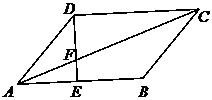
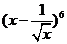 的展开式中的常数项是
(用数字作答)
的展开式中的常数项是
(用数字作答)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com