水位是指河流某处的水面海拔高度，一年中等于和大于某一水位出现的次数之和称为历时。读下面“水位过程线与历时曲线”图。回答9-11题。

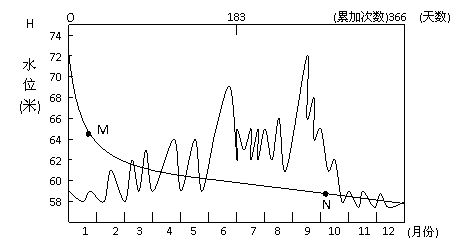
9．该河流的主要补给水源为(　 )

　 A．大气降水　　 B．季节性积雪融水　　 C．高山冰雪融水　 D．地下水

10．该观测站的位置最可能位于(　 )

　 A．青藏高原　　 B．黄土高原　　　 C．东北平原　　　 D．长江中下游平原

11．若在该测站上游修建一水库后，则历时曲线上的M、N点将(　 )

　 A．M、N同时右移　　　　　 B．M左移，N右移

C．M、N同时左移　　　　　 D．M右移，N左移

读“西北太平洋某季节气温与海水温度的差数分布”图，回答6-8题。

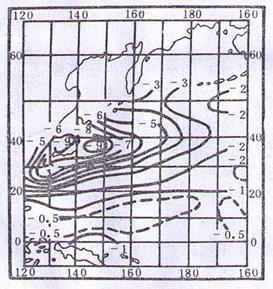
6．从图中可以看出，差数最大值位于(　 )

　 A．阿留申群岛附近　　　 B．日本海附近　 C．夏威夷群岛附近　 D．南海附近

7．图示情形出现的时间是(　 )

　 A．东北地区--千里冰封、万里雪飘　 　 B．华北地区--霜叶红于二月花

　 C．燕赵大地--赤日炎炎似火烧　 　　　 D．江淮地区--草长莺飞二月天

8．造成40°纬线附近西部差值大于东部的主要原因是(　 )

　 A．河川径流注入　　 B．洋流经过　 C．冬季风经过　 D．夏季风经过

读“日本国内运输结构的变化图”，回答4-5小题：

　　　　　 1965　 1985　　　　　　　　　　　　 1965　 1985

　　　　　 货运量构成　　　　　　　　　　　　　 客运量构成

4．有关日本国内运输构成变化特点的叙述正确的是(　 )

　 A．货运中水运的增长最快　　　　 　 B．客运中以铁路运输为主

C．铁路运输的客货量都明显下降　 　 D．铁路地位下降，公路运量明显提高

5．关于日本国内运输构成发生很大变化的原因叙述错误的是(　 )

　 A．汽车的机动性强，速度较快

　 B．国民收入水平的提高，小汽车拥有量的增加

　 C．发达的汽车工业及现代化的高速公路网

　 D．多山的岛国限制了铁路运输的发展

读某日北京时间9:00的晨昏线图(阴影部分表示夜)回答1-3小题：

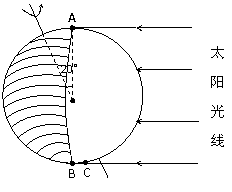
1．此时太阳直射点的地理坐标是(　 )

　 A．(20°N，15°W)　　　　 B．(0°，165°E)

C．(20°S，75°E)　　　　　　 D．(20°S，165°E)

2．此时C点的地方时及旗杆影子方位是(　 )

　 A．12时，正南　　　 B．0时，正北　　 C．12时，正北　　 D．0时，正南

3．图示季节，下列现象可能出现的是(　 )

　 A．在北印度洋护航船上的红旗飘向东北

　 B．在青海湖畔有大批游人在观鸟

　 C．在南极大陆上中国科考人员正在科学考察

　 D．在澳大利亚牧场上正忙于剪羊毛

22、(14分) 已知F₁、F₂分别是椭圆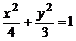的左、右焦点，曲线C是以坐标原点为顶点，以F₂为焦点的抛物线，自点F₁引直线交曲线C于P、Q两个不同的点，点P关于x轴对称的点记为M，设.

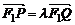(1)写出曲线C的方程；

(2)若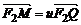，试用λ表示u；

21、(12分)已知定义域为R的二次函数f(x)的最小值为0，且有f(1+x)＝f(1－x), 直线g(x)＝4(x－1)的图象被f(x)的图象截得的弦长为4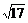，数列{a_n}满足a₁＝2,

(a_n+1－a_n)g(a_n)+f(a_n)＝0 (n∈N*).

(1)求函数f(x)的解析式；

(2)求数列{a_n}的通项公式；

(3)设b_n＝3f(a_n)－g(a_n+1)，求数列{b_n}的最值及相应的n值。

20、(12分)已知函数f(x)＝x³―ax―1.

(1)若f(x)在实数集R上单调递增，求实数a的取值范围；

(2)是否存在实数a，使f(x)在(－1, 1)上单调递减？若存在，求出a的取值范围，若不存在，说明理由。

19、(12分)已知斜三棱柱ABC-A₁B₁C₁，侧面ACC₁A₁与底面ABC垂直，

∠ABC＝90°，BC＝2，AC＝2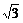，且AA₁⊥A₁C，AA₁＝A₁C.

(1)试判断AA₁与平面A₁BC是否垂直，并说明理由；

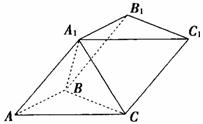(2)求侧面BB₁C₁C与底面ABC所成锐二面角的余弦值。

18、(12分)某工厂每月生产某种产品三件，经检测发现，工厂生产该产品的合格率为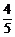，已知生产一件合格品能盈利25万元，生产一件次品将会亏损10万元，假设该产品任何两件之间合格与否相互没有影响。

(1)求工厂每月盈利额ξ(万元)的所有可能取值；

(2)若该工厂制定了每月盈利额不低于40万元的目标，求该工厂达到盈利目标的概率。

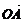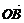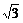17、(12分)已知x∈R, 向量＝(acos²x, 1), ＝(2, asin2x－a), f(x)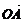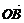＝·, a≠0.

(1)求函数f(x)的解析式，并求当a＞0时，f(x)的单调增区间；

(2)当x∈[0, 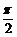]时，f(x)的最大值为5，求a的值。