
4、C(理)曲线在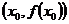 处有导数,则切线一定存在,但有切线,切线的斜率可能不存在,即导数不存在.
处有导数,则切线一定存在,但有切线,切线的斜率可能不存在,即导数不存在.
(文)该题一般都认为是选A,依照教科书上的结论:“一般地,设函数y=f(x)在某个区间内有导数,如果在这个区间内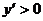 ,那么y=f(x)为这个区间内的增函数;如果在这个区间内
,那么y=f(x)为这个区间内的增函数;如果在这个区间内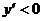 ,那么y=f(x)为这个区间内的减函数。”致错的原因是没有准确理解上述这段话的逻辑关系,事实上这是一个充分非必要条件。例如,函数f(x)=x3在(-∞,+∞)是单调递增的,然而却有
,那么y=f(x)为这个区间内的减函数。”致错的原因是没有准确理解上述这段话的逻辑关系,事实上这是一个充分非必要条件。例如,函数f(x)=x3在(-∞,+∞)是单调递增的,然而却有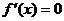 。
。
3、B由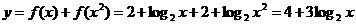 ,注意到为使得
,注意到为使得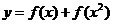 有意义必有
有意义必有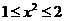 得
得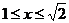 ,从而
,从而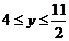 .
.
2、B设指数函数和对数函数分别为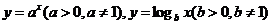 .若为"好点",则
.若为"好点",则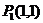 在
在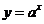 上,得
上,得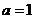 与
与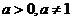 矛盾;
矛盾;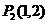 显然不在
显然不在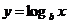 ;
;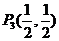 在
在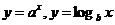 上时
上时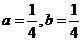 ,易得
,易得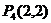 也为"好点"
也为"好点"
1、A本题考查中介法和单调性法比较大小,log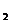
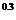 <0,而其他两个都大于零,至于a和b,构造中介0.3
<0,而其他两个都大于零,至于a和b,构造中介0.3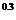 或2
或2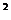 ,然后分别利用指数函数和幂函数的单调性比较,例如2
,然后分别利用指数函数和幂函数的单调性比较,例如2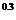 >0.3
>0.3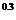 >0.3
>0.3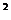
21、三次函数f(x)=x3+ax2+bx+a2在x=1处有极值0
①求函数f(x)的解析式
②求它的对称中心的横坐标(无需证明)
③(理)过异于对称中心的任一点P1(x1,y1)作f(x)图像的切线,切于另一点P2(x2,y2),再过P2(x2,y2)作f(x)图像的切线,和f(x)切于点P3(x3,y3),如此下去,得到P4(x4,y4)、P5(x5,y5)、···、Pn(xn,yn),求当次数n不断增大时Pn 的横坐标趋近于哪一个数?
专题一 函数与导数 答案
20、已知函数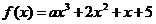 ,a为常数。如果对任意的
,a为常数。如果对任意的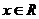 ,不等式
,不等式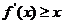 恒成立,求实数a的取值范围。
恒成立,求实数a的取值范围。
19、设x ∈[0 ,1 ] , f ( x ) =
x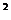 - ax +
- ax +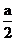 ( a ≥0) ,f(x)在定义域上的最小值记为F(x),试求F( a) 的最大值.
( a ≥0) ,f(x)在定义域上的最小值记为F(x),试求F( a) 的最大值.
18、李佳在2009年底购买了一套住房,经与房产公司协商,房款可在购房一年后(即2010年底)一次性付清,但要另付年利率为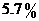 的利息。这时(2009年底)一家银行推出一款年利率低于
的利息。这时(2009年底)一家银行推出一款年利率低于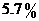 的一年期贷款业务,贷款额与利率的平方成正比,比例系数为k(k>0),李佳考虑申请这种贷款以便在购房时付清房款。
的一年期贷款业务,贷款额与利率的平方成正比,比例系数为k(k>0),李佳考虑申请这种贷款以便在购房时付清房款。
①若贷款的年利率为x,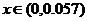 ,写出贷款额g(x)与利息h(x)的函数关系式
,写出贷款额g(x)与利息h(x)的函数关系式
②当贷款的年利率为多少时,李佳可以节省最多的钱
17、偏导数的概念:设有二元函数z=f(x,y),点(x0,y0)是其定义域内一点. 函数在(x0,y0)处对x的偏导数,实际上就是把y固定在y0看成常数后,一元函数z=f(x,y0)在x0处的导数,函数在(x0,y0)处对y的偏导数也是相同道理,分别记为f'x(x0,y0)和f'y(x0,y0)。已知函数z= x2+ y2
①分别求f'x(3,4)和f'y(3,4)
②如果f'x(3,4)x+f'y(3,4)y+1=0,求z的最小值
16、已知函数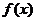 是定义在
是定义在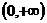 上的增函数,对任意
上的增函数,对任意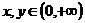 有
有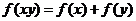 ,且
,且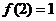
①求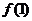 的值
的值
②解不等式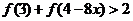
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com